景点旅游信息系统——C/C++程序设计、Qt图形化界面
一个 Qt、C/C++ 程序设计项目
文章目录
- 一、简单的效果演示
- 二、系统要求
- 三、系统设计
- 四、框架搭建
- 五、算法设计
-
- 5.1 创建景区景点分布图的算法:
- 5.2 判断创建的导游线路图有无回路的算法——拓扑图:
- 5.3 输出给定入口景点的导游线路图的算法——DFS
- 5.4 求两个景点间的最短路径的算法——Floyd
- 5.5 给出道路建设(最小生成树)的算法——Kruskal
- 六、测试数据及其结果分析
- 七、完整代码
- 八、参考附录
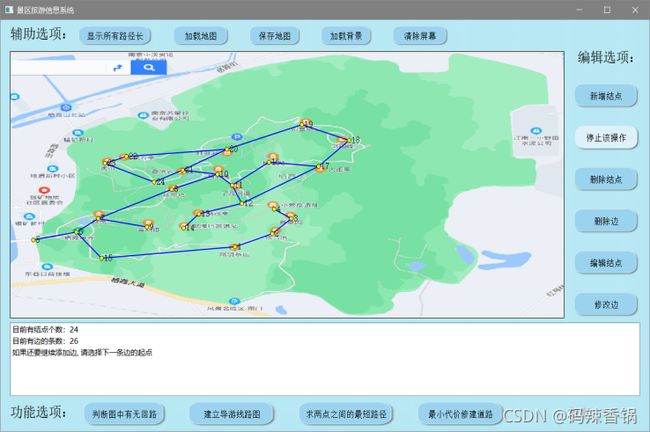
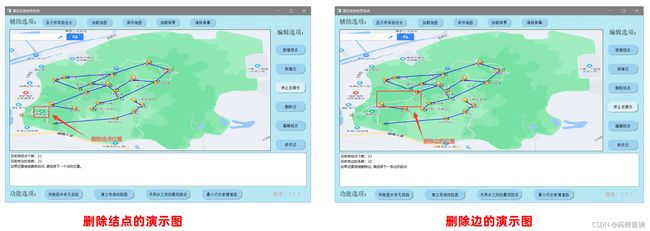
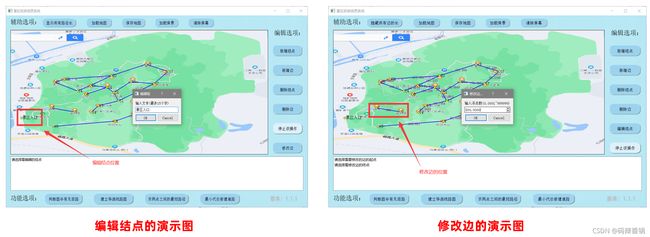
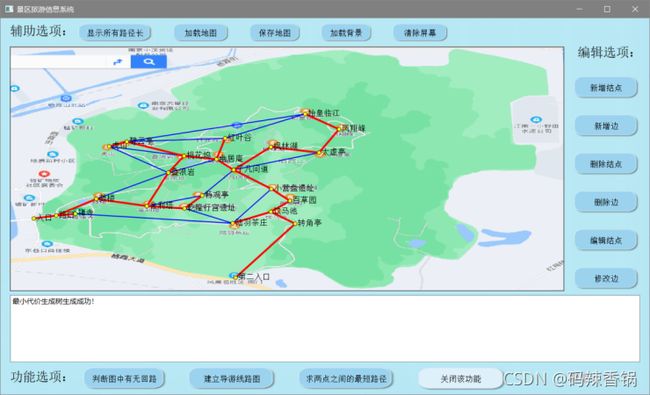
一、简单的效果演示
● 说明:简单演示了一下新增/删除结点和边,以及一些功能按钮。
二、系统要求
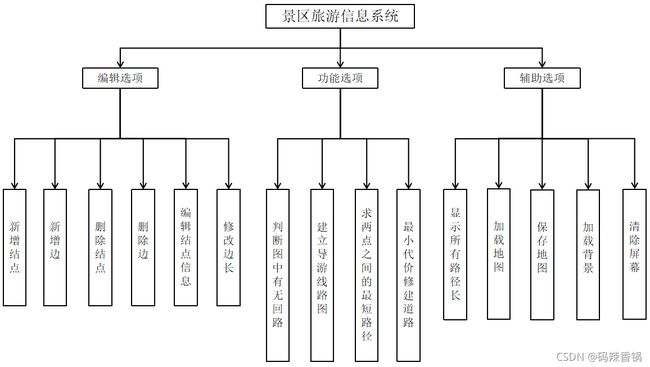
● 景区旅游信息系统,需要实现的功能有如下 4 项:
(1) 能自行建立一个导游线路地图。能通过拓朴排序判断图中有无回路,若有回路,则打印输出回路中的景点。
(2) 若给出一个入口景点,能自行采用深度优先策略建立一个导游线路图。
(3) 在导游线路图中,能实现查看从一个景点到另一个景点的最短路径。
(4) 景区道路能保证连通所有景点,且能通过最小代价生成树的策略来修建道路(代价只与它的里程有关)。
三、系统设计
四、框架搭建
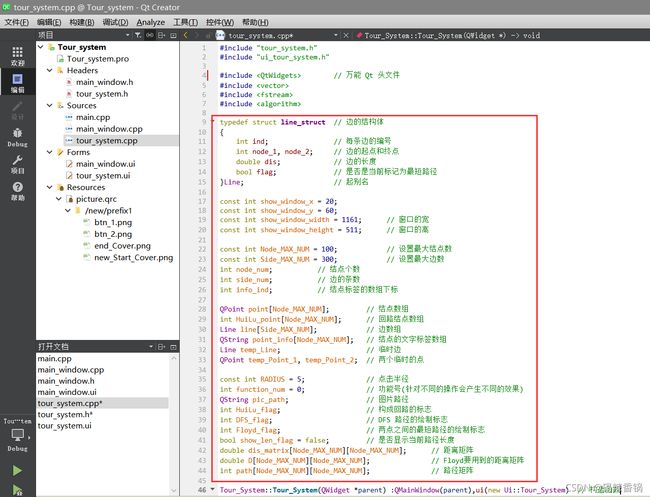
● 项目管理如下:
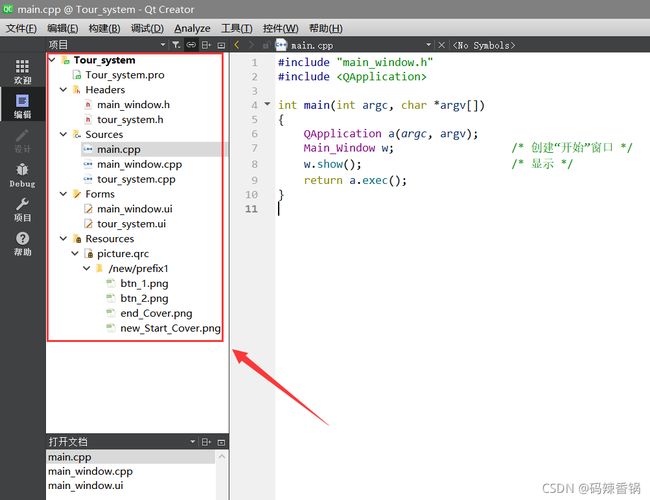
● 说明:
① main.cpp 是主函数入口。
② main_window.cpp 是 “开始” 界面的源代码。
③ tour_system.cpp 是景区旅游信息系统的源代码 。
● 头文件tour_system.h 如下:
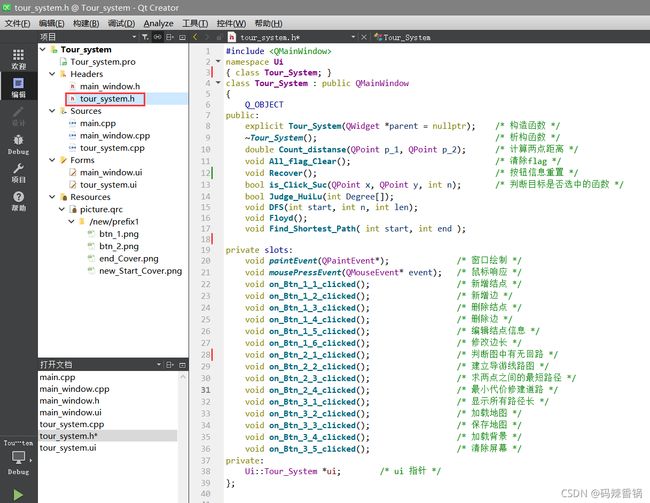
● 说明【这段话很关键】:其中主要反复调用的函数是mousePressEvent(),即 “鼠标相应函数”。因为我们在进行相关图形操作时,都是以 “点” 为基本操作对象(若是要确定一条边,也是点击某两个点。若要进行某项功能,也是点击相应的功能按钮一下)。所以我们主要在mousePressEvent()写 “景区系统的主核心舱”,配合switch()语句来实现对各个功能的反复调用。
● mousePressEvent()的 框架版代码 如下:
void Tour_System::mousePressEvent(QMouseEvent* e) // 鼠标点击事件
{
if (e->button() == Qt::LeftButton) // 按左键
{
switch(function_num)
{
case 1: // 添加点
function_num = 0; // 执行完后归零
...
break;
case 2: // 新增边(选择边的起点)
function_num = 3;
...
break;
case 3: // 新增边(选择边的终点)
function_num = 0;
...
break;
case 4: // 删除结点
function_num = 0;
...
break;
case 5: // 删除边(选择边的起点)
function_num = 6;
...
break;
case 6: // 删除边(选择边的终点)
function_num = 0;
...
break;
case 7: // 编辑结点的标签
function_num = 0;
...
break;
case 8: // 修改边(选择边的起点)
function_num = 9;
...
break;
case 9: // 修改边(选择边的终点)
function_num = 0;
...
break;
case 10: // 建立导游路线图(DFS)
function_num = 0;
...
break;
case 11: // 求两点之间的最短路径(Floyd)——选择起点
function_num = 12;
...
break;
case 12: // 求两点之间的最短路径(Floyd)——选择终点
...
break;
}
}
}
void Tour_System::on_Btn_1_1_clicked() // 新增结点
{
function_num = 1
...
}
void Tour_System::on_Btn_1_2_clicked() // 新增边
{
function_num = 2
...
}
void Tour_System::on_Btn_1_3_clicked() // 删除结点
{
function_num = 4
...
}
void Tour_System::on_Btn_1_4_clicked() // 删除边
{
function_num = 5
...
}
void Tour_System::on_Btn_1_5_clicked() // 编辑结点
{
function_num = 7
...
}
void Tour_System::on_Btn_1_6_clicked() // 修改边
{
function_num = 8
...
}
void Tour_System::on_Btn_2_1_clicked() // 判断是否有回路
{
... }
void Tour_System::on_Btn_2_2_clicked() // 建立一张导游线路图(DFS)
{
function_num = 10
...
}
void Tour_System::on_Btn_2_3_clicked() // 求两点之间的最短路径(Floyd)
{
function_num = 11
...
}
void Tour_System::on_Btn_2_4_clicked() // 最小生成树(Kruskal)
{
... }
void Tour_System::on_Btn_3_1_clicked() // 显示所有边长
{
... }
void Tour_System::on_Btn_3_2_clicked() // 加载地图
{
... }
void Tour_System::on_Btn_3_3_clicked() // 保存地图
{
... }
void Tour_System::on_Btn_3_4_clicked() // 加载背景
{
... }
void Tour_System::on_Btn_3_5_clicked() // 清除屏幕
{
... }
五、算法设计
● 在写算法之前,先把所有要用到的全局变量展示出来,如下图所示:
5.1 创建景区景点分布图的算法:
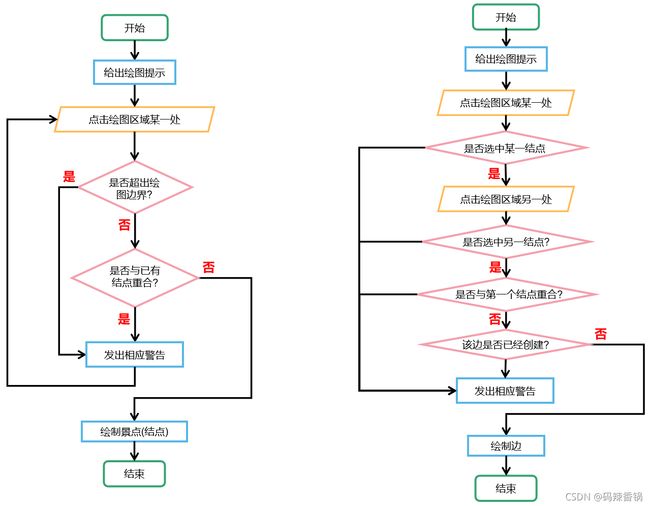
● 运用绘图函数paintEvent()和鼠标点击响应函数mousePressEvent()来处理景区景点以及道路的绘制与连接。
● 景点的绘制机制:鼠标点击处所在的小圆域(半径自行设置),如果没有其他已创建的景点(结点),那么将新生成并绘制该景点(结点)。
● 道路的绘制机制:用鼠标选取两个景点(结点),即可新生成一条景区道理,并会赋予该道路相应的结构体成员信息。
● 代码如下:
void Tour_System::mousePressEvent(QMouseEvent* e) // 鼠标点击事件
{
if (e->button() == Qt::LeftButton) // 按左键
{
QPoint cur_click_pos = e->pos(); // e->pos(): 获取当前点击位置
switch(function_num)
{
case 1: // 添加点
if(node_num < Node_MAX_NUM && cur_click_pos.x() >= show_window_x &&
cur_click_pos.x() <= show_window_x+show_window_width &&
cur_click_pos.y() >= show_window_y && cur_click_pos.y() <= show_window_y+show_window_height)
// 判断所加的点是否在窗口范围内
{
int save_node_num = node_num;
node_num++;
for(int i = 1; i < node_num; i++)
{
if(is_Click_Suc(cur_click_pos, point[i], RADIUS+10)) // 判断鼠标所点击位置和图上所有已添加的结点位置,是否靠的太近
{
node_num--;
QMessageBox::warning(this, "警告", "两个点靠太近!");
}
}
if(save_node_num == node_num)
break;
point[node_num] = e->pos(); // 当前位置赋给最新的结点
point_info[node_num] = QString::number(++info_ind); // 创建默认标签
update();
}
else if(node_num >= Node_MAX_NUM)
{
QMessageBox::warning(this, "警告", "目前结点数已达上限,无法再继续添加!");
}
else
{
QMessageBox::warning(this, "警告", "新加结点已超出边界!");
}
ui->Message_1->clear();
ui->Message_1->addItem("目前有结点个数:" + QString::number(node_num));
ui->Message_1->addItem("目前有边的条数:" + QString::number(side_num));
ui->Message_1->addItem("如果还要继续添加, 请选择下一个点的位置。");
function_num = 1; // 功能号 1 保持不变(便于重复添加点)
break;
case 2: // 新增边(选择边的起点)
if(side_num >= Side_MAX_NUM)
{
QMessageBox::warning(this, "警告", "路径数已达上限!");
}
else
{
for( int i = 1; i <= node_num; i++ )
{
if( is_Click_Suc(cur_click_pos, point[i], RADIUS) ) // 判断是否选中
{
function_num = 3; // 找到了新增边的起点后, 还需找到其终点. 故把控制权交给功能号3
temp_Point_1 = point[i];
line[side_num + 1].node_1 = i;
ui->Message_1->clear();
ui->Message_1->addItem("请选择边的终点位置");
break;
}
}
}
update();
break;
case 3: // 新增边(选择边的终点)
for( int i = 1; i <= node_num; i++ )
{
if(point[i] != temp_Point_1 && is_Click_Suc(cur_click_pos, point[i], RADIUS)) // 若选中了与第一个点不同的点
{
function_num = 2; // 重新把控制权交给功能号2(便于重复添加“边”)
int save_side_num = side_num++; // 线数量 + 1
temp_Point_2 = point[i];
line[side_num].node_2 = i;
if(line[side_num].node_1 > line[side_num].node_2) // 确保边的起点下标比终点的小, 不然做交换
{
int temp = line[side_num].node_1;
line[side_num].node_1 = line[side_num].node_2;
line[side_num].node_2 = temp;
}
for( int j = 1; j < side_num; j++ ) // 判断是否路线已经存在
{
if(line[side_num].node_1 == line[j].node_1 && line[side_num].node_2 == line[j].node_2)
{
line[side_num] = line[0];
side_num--;
QMessageBox::warning(this, "警告", "该路径已添加!");
break;
}
}
if(save_side_num != side_num) // 如果路该线之前在图中不存在, 则该表达式成立
{
int ind_1 = line[side_num].node_1;
int ind_2 = line[side_num].node_2;
dis_matrix[ind_1][ind_2] = dis_matrix[ind_2][ind_1] = Count_distanse(point[ind_1], point[ind_2]); // 距离矩阵赋值
line[side_num].ind = side_num; // 边的“编号”
line[side_num].dis = Count_distanse(point[ind_1], point[ind_2]); // 边的长度
}
ui->Message_1->clear();
ui->Message_1->addItem("目前有结点个数:" + QString::number(node_num));
ui->Message_1->addItem("目前有边的条数:" + QString::number(side_num));
ui->Message_1->addItem("如果还要继续添加边, 请选择下一条边的起点");
break;
}
}
update();
break;
case 4: // 删除结点
...
...
}
}
}
void Tour_System::on_Btn_1_1_clicked() // 新增结点
{
All_flag_Clear(); // 标签清空操作
Recover(); // 按钮信息重置
if(function_num != 1)
{
function_num = 1;
ui->Btn_1_1->setStyleSheet("border-image: url(:/new/prefix1/btn_2.png);");
ui->Btn_1_1->setText("停止该操作");
ui->Message_1->clear();
ui->Message_1->addItem("请选择一个位置添加新结点");
}
else
{
function_num = 0;
ui->Btn_1_1->setText("新增结点");
ui->Message_1->clear();
}
}
void Tour_System::on_Btn_1_2_clicked() // 新增边
{
All_flag_Clear(); // 标签清空操作
Recover(); // 按钮信息重置
if(function_num != 2)
{
function_num = 2;
ui->Btn_1_2->setStyleSheet("border-image: url(:/new/prefix1/btn_2.png);");
ui->Btn_1_2->setText("停止该操作");
ui->Message_1->clear();
ui->Message_1->addItem("请选择新增边的起点");
}
else
{
function_num = 0;
ui->Btn_1_2->setText("新增边");
ui->Message_1->clear();
}
}
5.2 判断创建的导游线路图有无回路的算法——拓扑图:
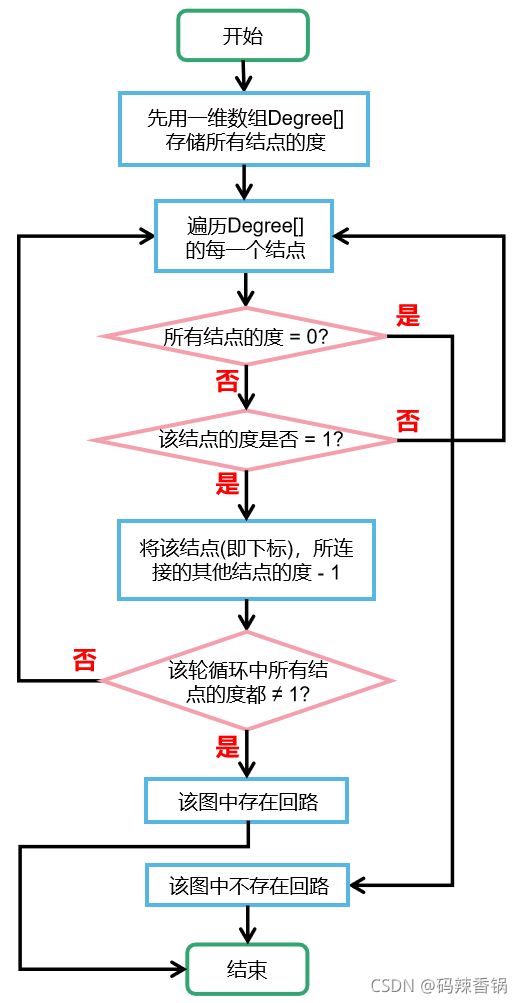
● 算法思路:
[1]采用拓扑排序,先用一维数组存储所有结点的度(数组下标设为结点对应的序号)
[2]每有一条边,与之相连的结点的度数就加 1
[3]然后我们进行遍历,将度数为 1 的结点删去(与之相连的边也要删去)
[4]数组也要随之更新,删去的那条边所相连的结点的度数 - 1
[5]如果已没有符合条件的结点被删去,则跳到[5],否则转向[2]
[6]如果还有数组中还有数,那么打印出它们即是存在回路的几个结点。
时间复杂度:O(n^2)
bool Tour_System::Judge_HuiLu(int Degree[])
{
/* 初始化操作 */
for( int i = 0; i <= node_num ; i++ )
HuiLu_point[i] = 0;
HuiLu_flag = 0;
/* 以上这部分很重要 */
for(int i = 1; i <= node_num; i++)
{
Degree[i] = 0;
}
for(int i = 1; i <= node_num; i++)
{
for(int j = i+1 ; j <= node_num; j++)
{
if( dis_matrix[i][j] != 0 )
{
Degree[i]++;
Degree[j]++;
}
}
}
int Btn_2_1_flag = 1;
int node_num_record = 0;
while( Btn_2_1_flag )
{
Btn_2_1_flag = 0; // 如果没有满足条件的结点存在则跳出循环
for( int i = 1; i <= node_num; i++ )
{
if( Degree[i] == 1 ) // 每轮循环只对度数为 1 的结点做处理
{
Degree[i] = 0;
Btn_2_1_flag = 1;
node_num_record++;
for( int j = 1; j <= node_num; j++ )
{
if( dis_matrix[i][j] != 0 )
{
Degree[j]--;
break;
}
}
}
}
}
if( node_num_record != node_num )
return true;
else
return false;
}
void Tour_System::on_Btn_2_1_clicked() // 判断是否有回路
{
All_flag_Clear();
Recover();
if(function_num != 13)
{
function_num = 13;
ui->Btn_2_1->setStyleSheet("border-image: url(:/new/prefix1/btn_2.png);");
ui->Btn_2_1->setText("停止该操作");
int Degree[Node_MAX_NUM+1];
if( Judge_HuiLu(Degree) )
{
QString str = "";
int first = 0;
int cnt = 1;
for( int i = 1; i <= node_num ; i++ )
{
if( Degree[i] > 0 && first == 0 )
{
str = str + point_info[i];
first = 1;
HuiLu_point[cnt++] = i;
}
else if( Degree[i] > 0 && first != 0 )
{
str = str + "," + point_info[i];
HuiLu_point[cnt++] = i;
}
}
str = "存在回路的结点(结点标签为):" + str;
HuiLu_flag = 1;
ui->Message_1->addItem(str);
}
else
{
function_num = 0;
ui->Message_1->addItem("该图中无回路");
}
}
else
{
function_num = 0;
ui->Btn_2_1->setText("判断是否有回路");
ui->Message_1->clear();
}
}
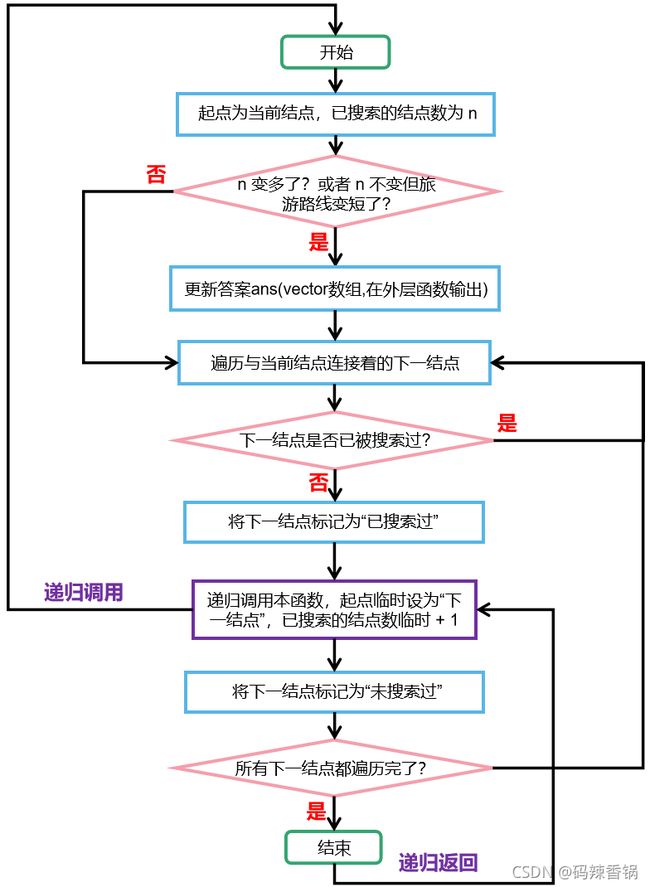
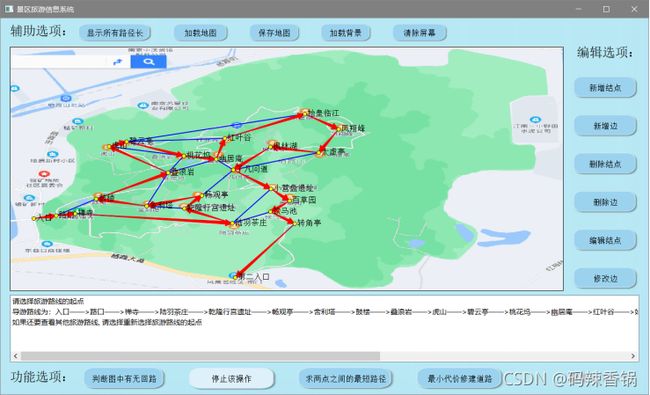
5.3 输出给定入口景点的导游线路图的算法——DFS
● 算法思路如下:
[1]首先设定每个结点最多只能被访问一次(有些结点所处的位置可能是“死胡同”)
[2]用一维的vector来储存结果, 单元依次存储路径结点的info(标签).
[3]采用DFS方式进行搜索, 每搜索到一个结点就放入当前的vector里面
[4]发生递归(两种情况:<1>搜完了所有结点;<2>搜索失败), 注意对vector的调整
[5]每次调用该函数时,都会进行“性能”比较,会将“好路线”更新到ans里面
[6]最后输出对应ans最后一组结点信息即可。
int vis[Node_MAX_NUM];
int cur_max_node_num = 1;
int Shortest_path_len = 0;
int cnt;
QVector<QString> vec_1;
QVector<QString> ans_1[500];
QVector<QPoint> vec_2;
QVector<QPoint> ans_2[500];
void Tour_System::DFS(int start, int n, int len) // start 为入口编号, n 为已加入路径的(景点)结点个数, len 为当前累加路经长
{
if( n >= cur_max_node_num )
{
if( n > cur_max_node_num)
{
cur_max_node_num = n;
ans_1[cnt] = vec_1;
ans_2[cnt] = vec_2;
cnt++;
}
else if( len < Shortest_path_len )
{
ans_1[cnt] = vec_1;
ans_2[cnt] = vec_2;
cnt++;
}
}
for( int i = 1; i <= node_num; i++ )
{
if( dis_matrix[start][i] != 0 && vis[i] == 0 ) // 有路 + 未被访问过,那就可以下手了!
{
vis[i] = 1;
vec_1.push_back(point_info[i]);
vec_2.push_back(point[i]);
DFS(i, n+1, len+dis_matrix[start][i]);
vis[i] = 0;
vec_1.pop_back();
vec_2.pop_back();
}
}
}
void Tour_System::mousePressEvent(QMouseEvent* e) // 鼠标点击事件
{
if (e->button() == Qt::LeftButton) // 按左键
{
QPoint cur_click_pos = e->pos(); // e->pos(): 获取当前点击位置
switch(function_num)
{
...
case 10: // 建立导游路线图(DFS)
if( !(side_num >= 1 && node_num >= 2) )
{
QMessageBox::warning(this, "警告", "图中元素不满足实现该功能的前提条件!");
break;
}
/* 清零、清空操作 */
for( int i = 0 ; i <= node_num; i++ ) // 标记清零
vis[i] = 0;
if(!vec_1.isEmpty())
vec_1.clear(); // 清空
if(!vec_2.isEmpty())
vec_2.clear(); // 清空
cnt = 0;
for( int i = 0; i < 500; i++)
{
if(!ans_1[i].isEmpty())
ans_1[i].clear();
if(!ans_2[i].isEmpty())
ans_2[i].clear();
}
cur_max_node_num = 1;
DFS_flag = 0;
/* 以上这部分很重要 */
for (int i = 1; i <= node_num; i++)
{
if (is_Click_Suc(cur_click_pos, point[i], RADIUS))
{
vec_1.push_back(point_info[i]);
vec_2.push_back(point[i]);
vis[i] = 1;
Shortest_path_len = 0;
DFS(i, 1, 0);
QString str = "";
for( int i = 0; i < ans_1[cnt-1].size(); i++ )
{
if( i == 0 )
{
str = "导游路线为:" + ans_1[cnt-1][i];
}
else
{
str = str + "——>" + ans_1[cnt-1][i];
}
}
ui->Message_1->addItem(str);
DFS_flag = 1;
update();
break;
}
}
ui->Message_1->addItem("如果还要查看其他旅游路线, 请选择重新选择旅游路线的起点");
break;
case 11: // 求两点之间的最短路径(Floyd)——选择起点
...
...
} // end for if(鼠标左键点击成功)
} // end for swtch(...)
} // end for mousePressEvent(...)
void Tour_System::on_Btn_2_2_clicked() // 建立一张导游线路图(DFS)
{
All_flag_Clear();
Recover();
if(function_num != 10)
{
function_num = 10;
ui->Btn_2_2->setStyleSheet("border-image: url(:/new/prefix1/btn_2.png);");
ui->Btn_2_2->setText("停止该操作");
ui->Message_1->addItem("请选择旅游路线的起点");
}
else
{
function_num = 0;
ui->Btn_2_2->setText("建立导游线路图");
ui->Message_1->clear();
}
}
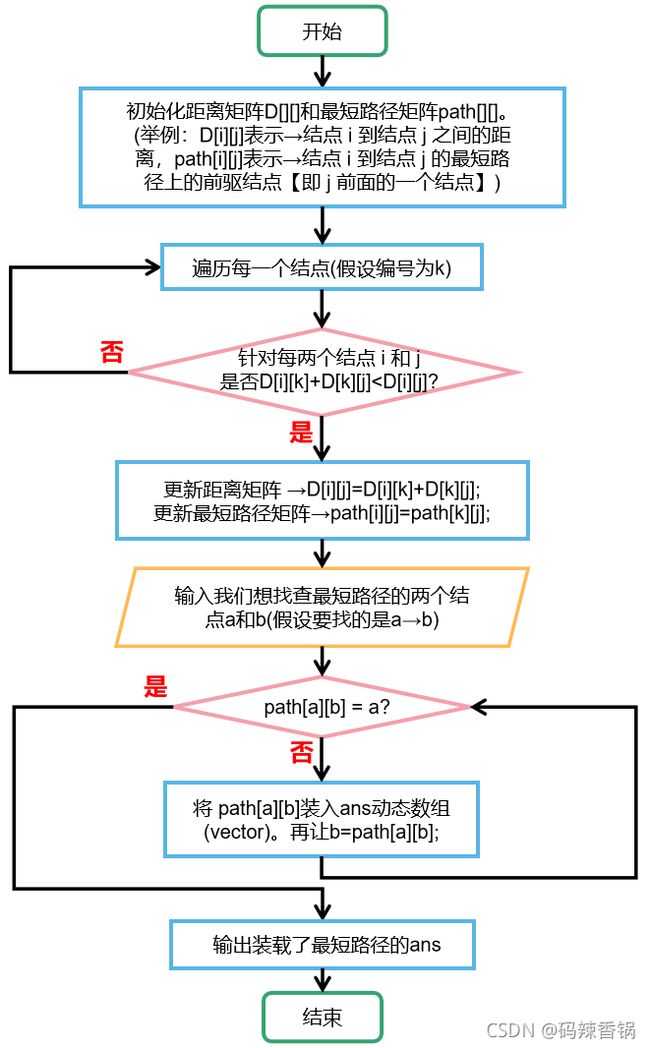
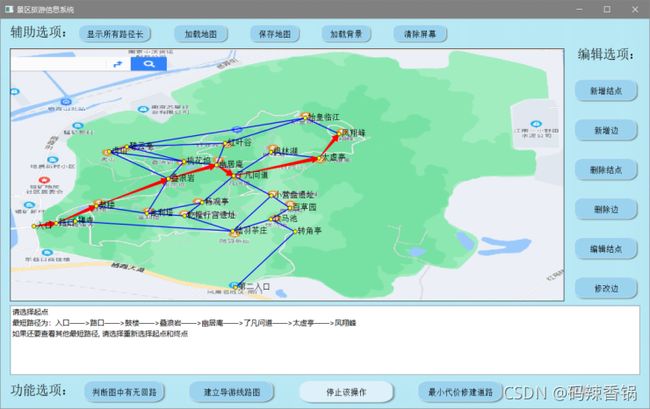
5.4 求两个景点间的最短路径的算法——Floyd
● 算法思路如下:
[1]初始化距离矩阵和路径矩阵
[2]依次加入每一个结点, 加入后更新距离矩阵和路径矩阵
[3]更新机制:
if( D[i][k]+D[k][j]<D[i][j])
{
D[i][j]=D[i][k]+D[k][j]; //更新矩阵
path[i][j]=path[k][j]; //更新路径
}
[4]最后再进行 “回溯” 输出最短路径即可(详见Find_Shortest_Path()函数)
void Tour_System::Floyd()
{
for( int i = 1; i <= node_num; i++ )
{
for( int j = 1; j <= node_num; j++ )
{
if( dis_matrix[i][j] == 0 )
D[i][j] = 999999; // 这里用999999假装代表无穷大
if( i == j )
D[i][i] = 0; // 自己到自己的距离是 0
if( i!=j && dis_matrix[i][j] != 0)
{
D[i][j] = dis_matrix[i][j];
path[i][j] = i; // 路径矩阵初始化
}
}
}
for( int k = 1; k <= node_num; k++ ) // 每次新“解封”一个结点
{
for( int i = 1; i <= node_num; i++ )
{
for( int j = 1; j <= node_num; j++ )
{
if( D[i][k] + D[k][j] < D[i][j] )
{
D[i][j] = D[i][k] + D[k][j]; // 动态更新距离矩阵
path[i][j] = path[k][j]; // 动态更新路径矩阵
}
}
}
}
}
void Tour_System::Find_Shortest_Path( int start, int end ) // 通过回溯法找出最短路径
{
vec_1.push_front(point_info[end]);
vec_2.push_front(point[end]);
while( start != end )
{
int add_ind = path[start][end];
vec_1.push_front(point_info[add_ind]);
vec_2.push_front(point[add_ind]);
end = path[start][end];
}
}
void Tour_System::mousePressEvent(QMouseEvent* e) // 鼠标点击事件
{
if (e->button() == Qt::LeftButton) // 按左键
{
QPoint cur_click_pos = e->pos(); // e->pos(): 获取当前点击位置
switch(function_num)
{
...
case 11: // 求两点之间的最短路径(Floyd)——选择起点
if( !(side_num >= 1 && node_num >= 2) )
{
QMessageBox::warning(this, "警告", "图中元素不满足实现该功能的前提条件!");
break;
}
/* 清零、清空操作 */
for( int i = 0 ; i <= node_num; i++ ) // 标记清零
vis[i] = 0;
if(!vec_1.isEmpty())
vec_1.clear(); // 清空
if(!vec_2.isEmpty())
vec_2.clear(); // 清空
cnt = 0;
for( int i = 0; i < 500; i++)
{
if(!ans_1[i].isEmpty())
ans_1[i].clear();
if(!ans_2[i].isEmpty())
ans_2[i].clear();
}
cur_max_node_num = 1;
DFS_flag = 0;
Floyd_flag = 0;
/* 以上这部分很重要 */
for(int i = 1; i <= node_num; i++)
{
if(is_Click_Suc(cur_click_pos, point[i], RADIUS))
{
function_num = 12; // 找到了起点后, 还需找到其终点. 故把控制权交给功能号12
temp_Point_1 = point[i];
temp_Line.node_1 = i; // 起点下标保存
break;
}
}
break;
case 12: // 求两点之间的最短路径(Floyd)——选择终点
...
} // end for if(鼠标左键点击成功)
} // end for swtch(...)
} // end for mousePressEvent(...)
void Tour_System::on_Btn_2_3_clicked() // 求两点之间的最短路径(Floyd)
{
All_flag_Clear();
Recover();
if(function_num != 11)
{
function_num = 11;
ui->Btn_2_3->setStyleSheet("border-image: url(:/new/prefix1/btn_2.png);");
ui->Btn_2_3->setText("停止该操作");
Floyd();
ui->Message_1->addItem("请选择起点");
}
else
{
function_num = 0;
ui->Btn_2_3->setText("求两点之间的最短路径");
ui->Message_1->clear();
}
}
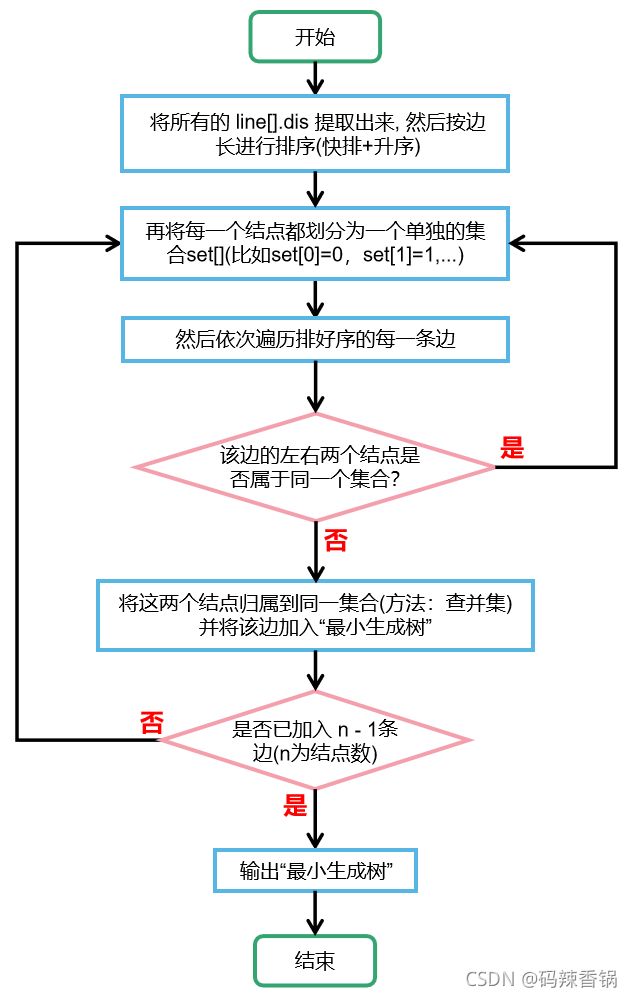
5.5 给出道路建设(最小生成树)的算法——Kruskal
● 算法思路如下:
[1]将所有的边提取出来, 然后按边长进行排序(快排+升序)
[2]再将每一个结点都划分为一个单独的集合(初始化)
[3]然后依次加边(按边长从小到大的顺序), 被连接在一起的结点归属到一个集合
[4]在加边过程中,加了这条边若会形成回路就跳过这条边(采用查并集算法)
[5]当所有的结点(n个)都被加入且在一个连通集合里面的时候, 把所有加入的边(n-1条)都输出出来, 图形界面展示即可
[6]最后给出景区建设中的能花最小的代价的道路建设。
int set[Node_MAX_NUM+1]; //每个结点属于的集合
int cmp( Line x, Line y )
{
return x.dis < y.dis;
}
int Find( int x )
{
if( x==set[x] )
return x;
return set[x]=Find(set[x]);
}
void He_bing( int x,int y )
{
int fx=Find(x),fy=Find(y);
set[fx]=fy;
}
void Tour_System::on_Btn_2_4_clicked() // 最小生成树(Kruskal)
{
All_flag_Clear();
Recover();
if(function_num != 14)
{
function_num = 14;
ui->Btn_2_4->setStyleSheet("border-image: url(:/new/prefix1/btn_2.png);");
ui->Btn_2_4->setText("停止该操作");
using namespace std;
/* 初始化操作 */
for( int i = 1; i <= node_num ; i++ )
set[i] = i;
/* 以上这部分很重要 */
Line new_Line[Side_MAX_NUM+1]; // 重新开一个数组, 这样就不会破坏原来的数组
for( int i = 0; i < side_num; i++ )
new_Line[i] = line[i+1];
std::sort(new_Line, new_Line+side_num, cmp);
int i = 0, cnt = 0;
QVector<int> vec;
while( cnt != node_num-1 )
{
if( i == side_num )
break;
int inital_ind = new_Line[i].ind;
int node_ind_1 = line[ inital_ind ].node_1;
int node_ind_2 = line[ inital_ind ].node_2;
if( Find(node_ind_1) != Find(node_ind_2) )
{
vec.push_back( inital_ind );
He_bing(node_ind_1, node_ind_2);
cnt++;
}
i++;
}
if( cnt != node_num-1 )
{
QMessageBox::warning(this, "警告", "该图不连通, 不存在最小代价生成树!");
}
else
{
for( int i = 0; i < node_num-1; i++ )
{
line[vec[i]].flag = 1;
}
QString str = "最小代价生成树生成成功!";
ui->Message_1->addItem(str);
ui->Btn_2_4->setText("关闭该功能");
update();
}
}
else
{
function_num = 0;
ui->Btn_2_4->setText("最小代价修建道路");
ui->Message_1->clear();
}
}
六、测试数据及其结果分析
● 登录界面如下:
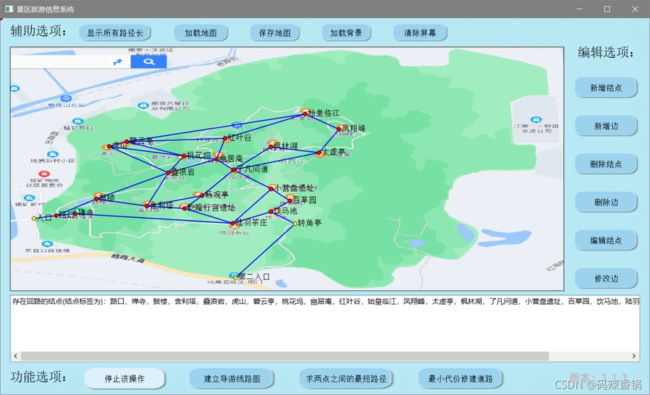
● 创建景区结点和道路:
● 编辑景区结点和边:
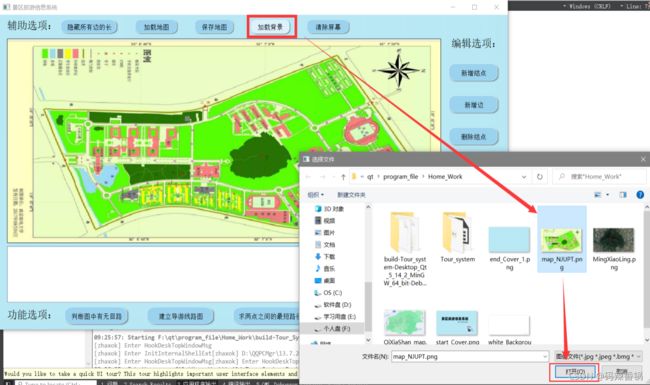
● 加载图片背景(无结点、边的数据):
● 注:加载地图功能和加载背景功能类似,只是多加了一个读文本文件的操作,而加载背景只读取限定后缀名的图片。保存地图功能是加载地图的反操作。清除屏幕功能即是把显示框里面的所有内容清除。这三个功能不方便用截图方式体现,详见源代码。
七、完整代码
● 可执行文件下载链接(百度云网盘,提取码: mlxg):https://pan.baidu.com/s/1eStv1uIHXjaMns_0JZY3eg.
● 项目文件源代码:https://download.csdn.net/download/Wang_Dou_Dou_/47693292.
八、参考附录
[1]《Qt5 开发及实例 第3版》 作者:陆文周
[2] Qt 5.14.2 下载、安装、使用教程,Qt+vs2019开发环境搭建
链接: https://www.bilibili.com/video/BV1r54y1G7m4.
[3] “地图”编辑器 之 程序演示【感谢南开大学的钔锌UP主,框架搭建主要参考了他的】
链接: https://www.bilibili.com/video/BV1k64y1W73o?spm_id_from=333.999.0.0.
⭐️ ⭐️