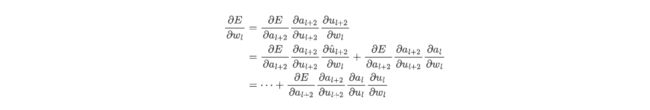深度学习-卷积神经网络(CNN)
- CNN基本原理
- 经典CNN
卷积神经网络基本原理
卷积神经网络的基本结构大致包括:卷积层、激活函数、池化层、全连接层、输出层等。
卷积层
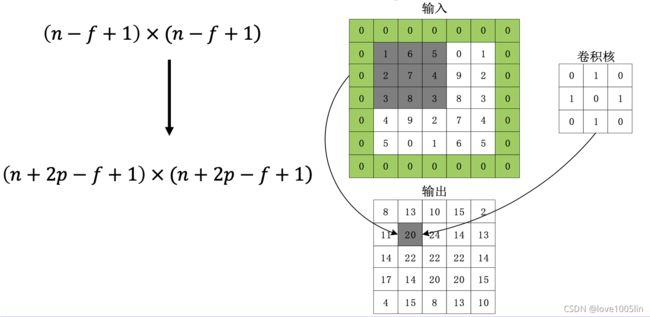
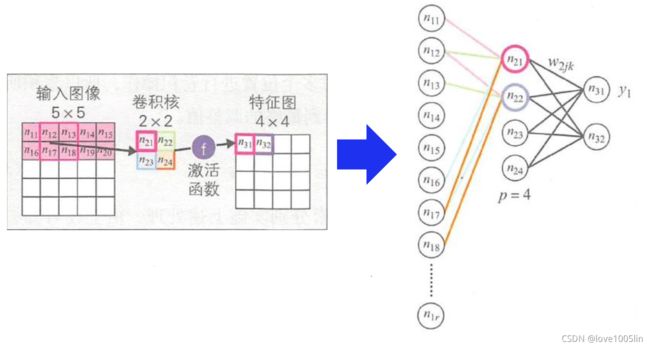
二维卷积运算:给定二维的图像I作为输入,二维卷积核K,卷积运算可表示为 S ( i , j ) = ( I ∗ K ) ( i , j ) = ∑ m ∑ n I ( i − m , j − n ) K ( m , n ) S(i, j)=(I * K)(i, j)=\sum_{m} \sum_{n} I(i-m, j-n) K(m, n) S(i,j)=(I∗K)(i,j)=∑m∑nI(i−m,j−n)K(m,n),卷积核需要进行上下翻转和左右反转
S ( i , j ) = sum ( I ( i − 2 , j − 2 ) I ( i − 2 , j − 1 ) I ( i − 2 , j ) I ( i − 1 , j − 2 ) I ( i − 1 , j − 1 ) I ( i − 1 , j ) I ( i , j − 2 ) I ( i , j − 1 ) I ( i , j ) ] . ∗ [ K ( 2 , 2 ) K ( 2 , 1 ) K ( 2 , 0 ) K ( 1 , 2 ) K ( 1 , 1 ) K ( 1 , 0 ) K ( 0 , 2 ) K ( 0 , 1 ) K ( 0 , 0 ) ] ) \left.S(i, j)=\operatorname{sum}\left(\begin{array}{ccc}I(i-2, j-2) & I(i-2, j-1) & I(i-2, j) \\ I(i-1, j-2) & I(i-1, j-1) & I(i-1, j) \\ I(i, j-2) & I(i, j-1) & I(i, j)\end{array}\right] . *\left[\begin{array}{rll}K(2,2) & K(2,1) & K(2,0) \\ K(1,2) & K(1,1) & K(1,0) \\ K(0,2) & K(0,1) & K(0,0)\end{array}\right]\right) S(i,j)=sum⎝⎛I(i−2,j−2)I(i−1,j−2)I(i,j−2)I(i−2,j−1)I(i−1,j−1)I(i,j−1)I(i−2,j)I(i−1,j)I(i,j)⎦⎤.∗⎣⎡K(2,2)K(1,2)K(0,2)K(2,1)K(1,1)K(0,1)K(2,0)K(1,0)K(0,0)⎦⎤⎠⎞
卷积实际上就是互相关
卷积的步长(stride):卷积核移动的步长
卷积的模式:Full**,** Same和Valid
数据填充:如果我们有一个 × 的图像,使用× 的卷积核进行卷积操作,在进行卷积操作之前我们在图像周围填充 层数据,输出的维度:
感受野:卷积神经网络每一层输出的特征图(featuremap)上的像素点在输 入图片上映射的区域大小,即特征图上的一个点对应输入图上的区 域。
那么如何计算感受野的大小,可以采用从后往前逐层的计算方法:
- 第 i 层的感受野大小和第 *i-*1 层的卷积核大小和步长有关系,同时也与第 (*i-*1)层感受野大小有关
- 假设最后一层(卷积层或池化层)输出特征图感受野的大小(相对于其直 接输入而言)等于卷积核的大小
卷积层的深度(卷积核个数):一个卷积层通常包含多个尺寸一致的卷积核
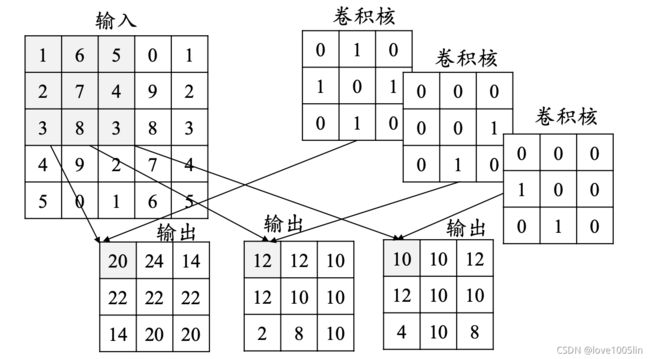
【卷积核的大小一般为奇数奇数】 11,33,55,77都是最常见的。这是为什么呢?为什么没有偶数偶数?
(1)更容易padding
在卷积时,我们有时候需要卷积前后的尺寸不变。这时候我们就需要用到padding。假设图像的大小,也就是被卷积对象的大小为nn,卷积核大小为kk,padding的幅度设为(k-1)/2时,卷积后的输出就为(n-k+2*((k-1)/2))/1+1=n,即卷积输出为n*n,保证了卷积前后尺寸不变。但是如果k是偶数的话,(k-1)/2就不是整数了。
(2)更容易找到卷积锚点
在CNN中,进行卷积操作时一般会以卷积核模块的一个位置为基准进行滑动,这个基准通常就是卷积核模块的中心。若卷积核为奇数,卷积锚点很好找,自然就是卷积模块中心,但如果卷积核是偶数,这时候就没有办法确定了,让谁是锚点似乎都不怎么好。
激活函数
激活函数是用来加入非线性因素,提高网络表达能力,卷积神经网络中最常用的是ReLU,Sigmoid使用较少。
1. ReLU函数
f ( x ) = { 0 , x < 0 x , x ≥ 0 f(x)=\left\{\begin{array}{l}0, x<0 \\ x, x \geq 0\end{array}\right. f(x)={ 0,x<0x,x≥0
ReLU函数的优点:
- 计算速度快,ReLU函数只有线性关系,比Sigmoid和Tanh要快很多
- 输入为正数的时候,不存在梯度消失问题
ReLU函数的缺点:
- 强制性把负值置为0,可能丢掉一些特征
- 当输入为负数时,权重无法更新,导致“神经元死亡”(学习率不 要太大)
2. Parametric ReLU
f ( x ) = { α x , x < 0 x , x ≥ 0 f(x)=\left\{\begin{array}{l}\alpha x, x<0 \\ x, x \geq 0\end{array}\right. f(x)={ αx,x<0x,x≥0
- 当 =0.01 时,称作Leaky ReLU
- 当 从高斯分布中随机产生时,称为Randomized ReLU(RReLU)
PReLU函数的优点:
- 比sigmoid/tanh收敛快
- 解决了ReLU的“神经元死亡”问题
PReLU函数的缺点:需要再学习一个参数,工作量变大
3. ELU函数
f ( x ) = { α ( e x − 1 ) , x < 0 x , x ≥ 0 f(x)=\left\{\begin{array}{l}\alpha (e^x-1), x<0 \\ x, x \geq 0\end{array}\right. f(x)={ α(ex−1),x<0x,x≥0
ELU函数的优点:
- 处理含有噪声的数据有优势
- 更容易收敛
ELU函数的缺点:计算量较大,收敛速度较慢
- CNN在卷积层尽量不要使用Sigmoid和Tanh,将导致梯度消失。
- 首先选用ReLU,使用较小的学习率,以免造成神经元死亡的情况。
- 如果ReLU失效,考虑使用Leaky ReLU、PReLU、ELU或者Maxout,此时一般情况都可以解决
特征图
- 浅层卷积层:提取的是图像基本特征,如边缘、方向和纹理等特征
- 深层卷积层:提取的是图像高阶特征,出现了高层语义模式,如“车轮”、“人脸”等特征
池化层
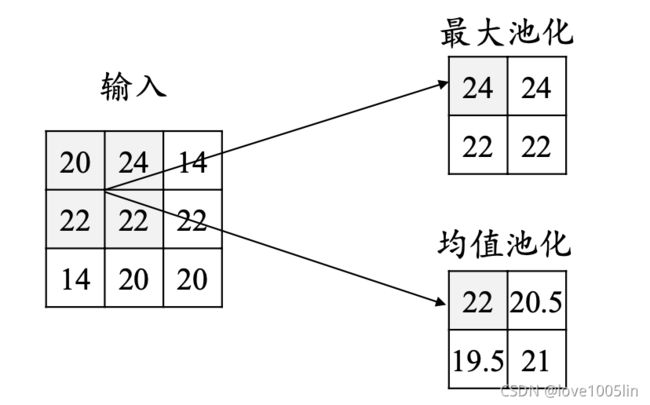
池化操作使用某位置相邻输出的总体统计特征作为该位置 的输出,常用最大池化**(max-pooling)和均值池化(average- pooling)**。
池化层不包含需要训练学习的参数,仅需指定池化操作的核大小、操作步幅以及池化类型。
池化的作用:
- 减少网络中的参数计算量,从而遏制过拟合
- 增强网络对输入图像中的小变形、扭曲、平移的鲁棒性(输入里的微 小扭曲不会改变池化输出——因为我们在局部邻域已经取了最大值/ 平均值)
- 帮助我们获得不因尺寸而改变的等效图片表征。这非常有用,因为 这样我们就可以探测到图片里的物体,不管它在哪个位置
全连接层
- 对卷积层和池化层输出的特征图(二维)进行降维
- 将学到的特征表示映射到样本标记空间的作用
输出层
对于分类问题:使用Softmax函数
y i = e z i ∑ i = 1 n e z i y_i = \frac{e^{z_i}}{\sum_{i = 1}^{n}e^{z_i}} yi=∑i=1neziezi
对于回归问题:使用线性函数
y i = ∑ m = 1 M w i m x m y_i = \sum_{m = 1}^{M}w_{im}x_m yi=m=1∑Mwimxm
卷积神经网络的训练
Step 1:用随机数初始化所有的卷积核和参数/权重
Step 2:将训练图片作为输入,执行前向步骤(卷积, ReLU,池化以及全连接层的前向传播)并计算每个类别的对应输出概率。
Step 3:计算输出层的总误差
Step 4:反向传播算法计算误差相对于所有权重的梯度,并用梯度下降法更新所有的卷积核和参数/权重的值,以使输出误差最小化
注:卷积核个数、卷积核尺寸、网络架构这些参数,是在 Step 1 之前就已经固定的,且不会在训练过程中改变——只有卷 积核矩阵和神经元权重会更新。
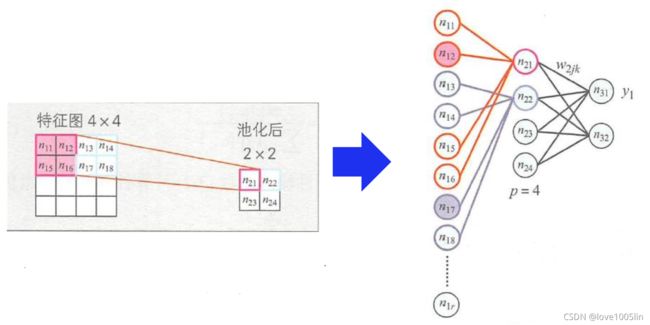
和多层神经网络一样,卷积神经网络中的参数训练也是使用误差反向传播算法,关于池化层的训练,需要再提一下,是将池化层改为多层神经网络的形式
将卷积层也改为多层神经网络的形式
计算卷积后特征图大小公式:
输入图片的尺寸:一般用n*n表示输入的image大小。
卷积核的大小:一般用 f*f 表示卷积核的大小。
填充(Padding):一般用 p 来表示填充大小。
步长(Stride):一般用 s 来表示步长大小。
输出图片的尺寸:一般用 o来表示。
如果已知n 、 f 、 p、 s 可以求得 o ,计算公式如下:

其中"[ ]"是向下取整符号,用于结果不是整数时进行向下取整。
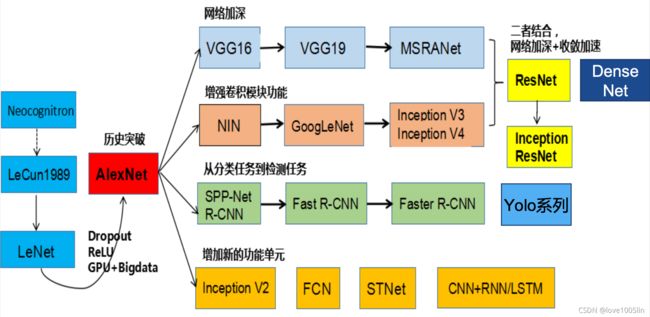
经典卷积神经网络
1. LeNet-5
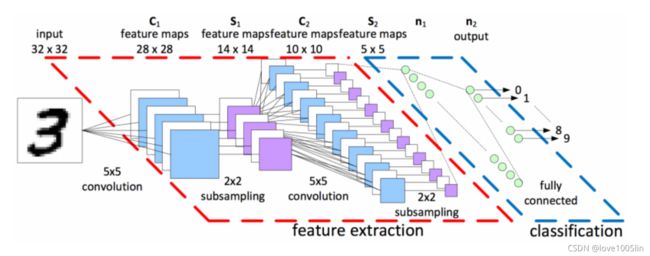
LeNet-5由LeCun等人提出于1998年提出,主要进行手写数字识别和英文字母识别。经典的卷积神经网络,LeNet虽小,各模块齐全,是学习 CNN的基础。
参考:http://yann.lecun.com/exdb/lenet/
Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, November 1998.
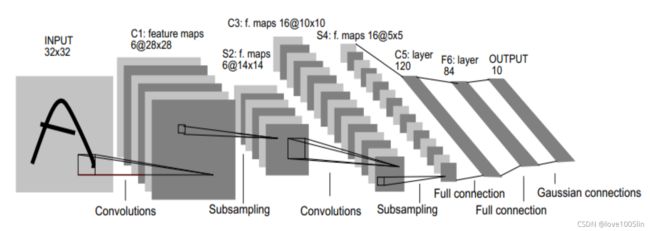
网络结构
输入层: 32 ∗ 32 32*32 32∗32 的图片,也就是相当于1024个神经元
C1层(卷积层):选择6个 5 ∗ 5 5*5 5∗5 的卷积核,得到6个大小为32-5+1=28的特征图,也就是神经元的个数为 6 ∗ 28 ∗ 28 = 4704 6*28*28=4704 6∗28∗28=4704
S2层(下采样层):每个下抽样节点的4个输入节点求和后取平均(平均池化),均值 乘上一个权重参数加上一个偏置参数作为激活函数的输入,激活函数的输出即是下一层节点的值。池化核大小选择 2 ∗ 2 2*2 2∗2,得到6个 14 ∗ 14 14*14 14∗14 大小特征图
C3层(卷积层):用 5 ∗ 5 5*5 5∗5的卷积核对S2层输出的特征图进行卷积后,得到6张 10 ∗ 10 10*10 10∗10 新 图片,然后将这6张图片相加在一起,然后加一个偏置项b,然后用 激活函数进行映射,就可以得到1张 10 ∗ 10 10*10 10∗10 的特征图。我们希望得到 16 张 10 ∗ 10 10*10 10∗10 的 特 征 图 , 因 此 我 们 就 需 要 参 数 个 数 为 16 ∗ ( 6 ∗ ( 5 ∗ 5 ) ) = 16 ∗ 6 ∗ ( 5 ∗ 5 ) 16*(6*(5*5))=16*6*(5*5) 16∗(6∗(5∗5))=16∗6∗(5∗5) 个参数
S4层(下采样层):对C3的16张 10 ∗ 10 10*10 10∗10 特征图进行最大池化,池化核大小为 2 ∗ 2 2*2 2∗2,得到16张大小为 5 ∗ 5 5*5 5∗5 的特征图。神经元个数已经减少为: 16 ∗ 5 ∗ 5 = 400 16*5*5=400 16∗5∗5=400
C5层(卷积层):用 5 ∗ 5 5*5 5∗5 的卷积核进行卷积,然后我们希望得到120个特征图,特征图 大小为5-5+1=1。神经元个数为120(这里实际上是全连接,但是原文还是称之为了卷积层)
F6层(全连接层):有84个节点,该层的训练参数和连接数都 ( 120 + 1 ) ∗ 84 = 10164 (120+1)* 84=10164 (120+1)∗84=10164
Output层:共有10个节点,分别代表数字0到9,如果节点i的输出值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式:
y i = ∑ j ( x − j − w i j ) 2 y_i = \sum_j(x-j - w_{ij})^2 yi=j∑(x−j−wij)2
总结:卷积核大小、卷积核个数(特征图需要多少个)、池化核大小(采样率多少)这些参数都是变化的,这就是所谓的CNN调参,需要学会根据需要进行不同的选择。
2. AlexNet
AlexNet由Hinton的学生Alex Krizhevsky于2012年提出,获得ImageNet LSVRC-2012(物体识别挑战赛)的冠军,1000个类别120万幅高清图像(Error: 26.2%(2011) →15.3%(2012)),通过AlexNet确定了CNN在计算机视觉领域的王者地位。
参考:A. Krizhevsky, I. Sutskever, and G. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012.
- 首次成功应用ReLU作为CNN的激活函数
- 使用Dropout丢弃部分神元,避免了过拟合
- 使用重叠MaxPooling(让池化层的步长小于池化核的大小), 一定程度上提升了特征的丰富性
- 使用CUDA加速训练过程
- 进行数据增强,原始图像大小为256×256的原始图像中重 复截取224×224大小的区域,大幅增加了数据量,大大减 轻了过拟合,提升了模型的泛化能力
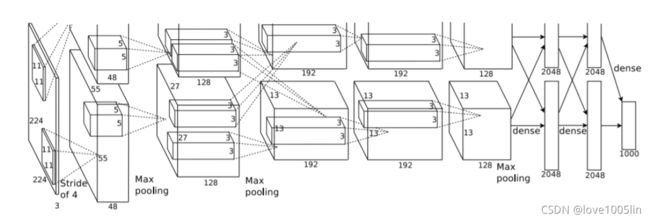
网络结构
AlexNet可分为8层(池化层未单独算作一层),包括5个卷 积层以及3个全连接层
输入层:AlexNet首先使用大小为224×224×3图像作为输入(后改为227×227×3) (227-11+2*0)/4+1=55
第一层(卷积层):包含96个大小为11×11的卷积核,卷积步长为4,因此第一层输出大小为55×55×96;然后构建一个核大小为3×3、步长为2的最大池化层进行数据降采样,进而输出大小为27×27×96
第二层(卷积层):包含256个大小为5×5卷积核,卷积步长为1,同时利用padding保证 输出尺寸不变,因此该层输出大小为27×27×256;然后再次通过 核大小为3×3、步长为2的最大池化层进行数据降采样,进而输出大小为13×13×256
第三层与第四层(卷积层):均为卷积核大小为3×3、步长为1的same卷积,共包含384个卷积核,因此两层的输出大小为13×13×384
第五层(卷积层):同样为卷积核大小为3×3、步长为1的same卷积,但包含256个卷积 核,进而输出大小为13×13×256;在数据进入全连接层之前再次 通过一个核大小为3×3、步长为2的最大池化层进行数据降采样, 数据大小降为6×6×256,并将数据扁平化处理展开为9216个单元
第六层、第七层和第八层(全连接层):全连接加上Softmax分类器输出1000类的分类结果,有将近6千万个参数
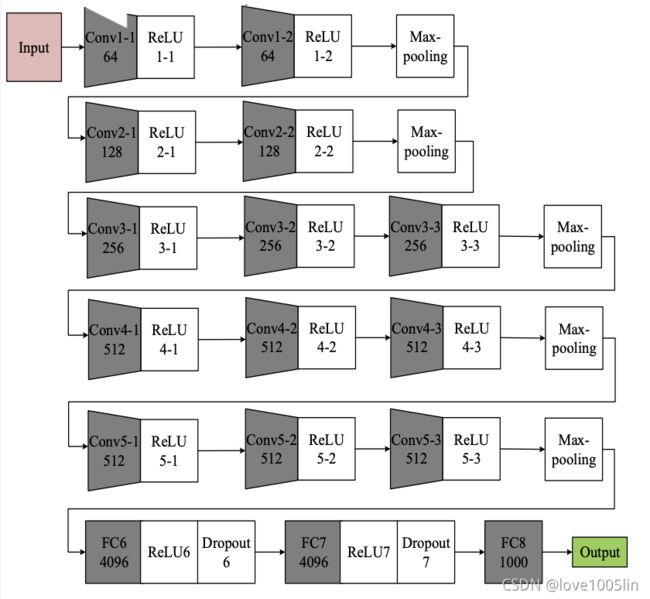
3. VGGNet
VGGNet由牛津大学和DeepMind公司提出
- Visual Geometry Group:https://www.robots.ox.ac.uk/~vgg/
- DeepMind:https://deepmind.com/
参考:K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. In ICLR, 2015.
- 比较常用的是VGG-16,结构规整,具有很强的拓展性
- 相较于AlexNet,VGG-16网络模型中的卷积层均使用 3 ∗ 3 3*3 3∗3 的 卷积核,且均为步长为1的same卷积,池化层均使用 2 ∗ 2 2*2 2∗2 的 池化核,步长为2
网络结构
- 两个卷积核大小为 3 ∗ 3 3*3 3∗3 的卷积层串联后的感受野尺寸为 5 ∗ 5 5*5 5∗5, 相当于单个卷积核大小为 5 ∗ 5 5*5 5∗5 的卷积层
- 两者参数数量比值为 ( 2 ∗ 3 ∗ 3 ) / ( 5 ∗ 5 ) = 72 % (2*3*3)/(5*5)=72\% (2∗3∗3)/(5∗5)=72% ,前者参数量更少
- 此外,两个的卷积层串联可使用两次ReLU激活函数,而一个卷积层只使用一次
4. Inception Net
Inception Net 是Google公司2014年提出,获得ImageNet LSVRC-2014冠军。文章提出获得高质量模型最保险的做法就是增加模型的深度(层数)或者是其宽度(层核或者神经元数),采用了22层网络。
Inception四个版本所对应的论文及ILSVRC中的Top-5错误率:
-
[v1] Going Deeper with Convolutions: 6.67%
-
[v2] Batch Normalization: Accelerating Deep Network Training by
Reducing Internal Covariate Shift: 4.8%
-
[v3]RethinkingtheInceptionArchitectureforComputerVision:3.5%
-
[v4] Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning: 3.08%
Inception Module
- 深度:层数更深,采用了22层,在不同深度处增加了两个 loss来避免上述提到的梯度消失问题
- 宽度:Inception Module包含4个分支,在卷积核3x3、5x5 之前、max pooling之后分别加上了1x1的卷积核,起到了降低特征图厚度的作用
- 1×1的卷积的作用:可以跨通道组织信息,来提高网络的表达能力;可以对输出通道进行升维和降维。
5. ResNet
ResNet(Residual Neural Network),又叫做残差神经网 络,是由微软研究院的何凯明等人2015年提出,获得ImageNet ILSVRC 2015比赛冠军,获得CVPR2016最佳论文奖。
随着卷积网络层数的增加,误差的逆传播过程中存在的梯 度消失和梯度爆炸问题同样也会导致模型的训练难以进行,甚至会出现随着网络深度的加深,模型在训练集上的训练误差会出现先降低再升高的现象。残差网络的引入则有助于解决梯度消失和梯度爆炸问题。
残差块
ResNet的核心是叫做残差块(Residual block)的小单元, 残差块可以视作在标准神经网络基础上加入了跳跃连接(Skip connection)
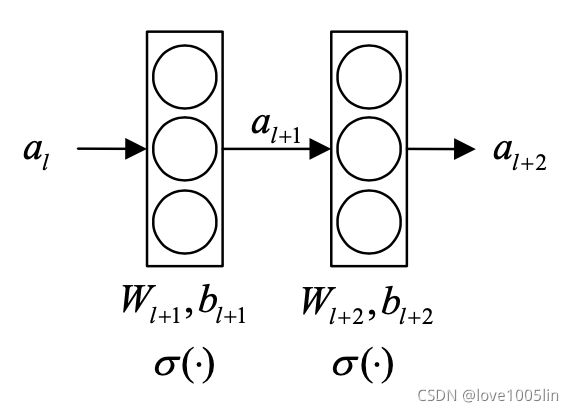
- 原连接
a l + 1 = σ ( W l + 1 a l + b l + 1 ) a l + 2 = σ ( W l + 2 a l + 1 + b l + 2 ) a_{l+1} = \sigma(W_{l+1}a_l+b_{l+1}) \\ a_{l+2} = \sigma(W_{l+2}a_{l+1}+b_{l+2}) al+1=σ(Wl+1al+bl+1)al+2=σ(Wl+2al+1+bl+2)
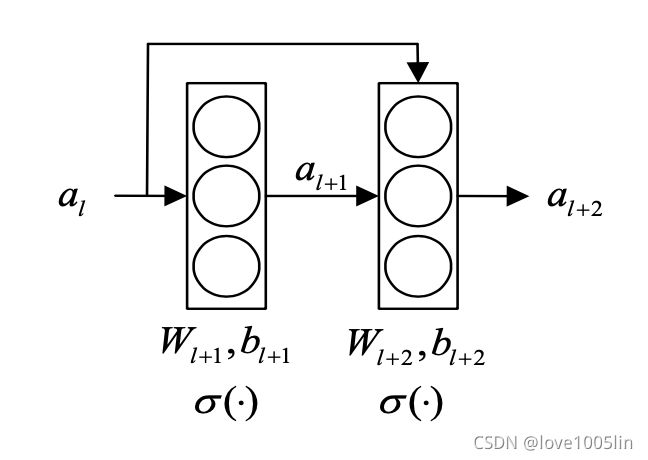
- 跳跃连接
a l + 1 = σ ( W l + 1 a l + b l + 1 ) a l + 2 = σ ( W l + 2 a l + 1 + b l + 2 + a l ) a_{l+1} = \sigma(W_{l+1}a_l+b_{l+1}) \\ a_{l+2} = \sigma(W_{l+2}a_{l+1}+b_{l+2}+a_l) al+1=σ(Wl+1al+bl+1)al+2=σ(Wl+2al+1+bl+2+al)
Skip connection的作用
记 u l + 1 = W l + 1 a l + b l + 1 , u l + 2 = W l + 2 a l + 1 + b l + 2 + a l = u ^ l + 2 + a l u_{l+1} = W_{l+1}a_l+b_{l+1},u_{l+2} = W_{l+2}a_{l+1}+b_{l+2}+a_l = \hat{u}_{l+2} + a_l ul+1=Wl+1al+bl+1,ul+2=Wl+2al+1+bl+2+al=u^l+2+al
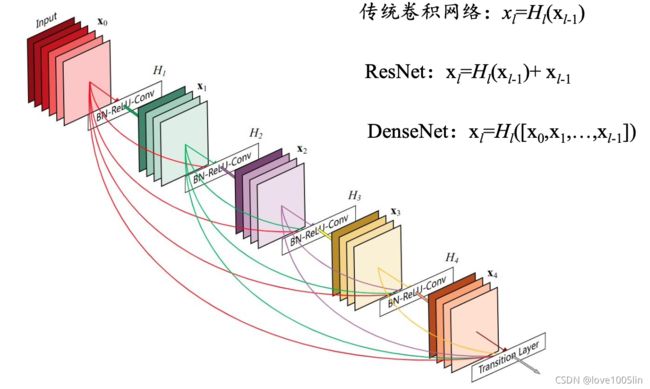
6. Densenet
DenseNet中,两个层之间都有直接的连接,因此该网络的直接连接个数为L(L+1)/2。
对于每一层,使用前面所有层的特征映射作为输入,并且使用其自身的特征映射作为所有后续层的输入
参考:Huang, G., Liu, Z., Van Der Maaten, L., & Weinberger, K. Q. (2017). Densely connected convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 4700- 4708).
5层的稠密块示意图
DenseNets可以自然地扩展到数百个层,而没有表现出优化困难。在实验中,DenseNets随着参数数量的增加,在精度上产生一致的提高,而没有任何性能下降或过拟合的迹象。
优点:
- 缓解了消失梯度问题
- 加强了特征传播,鼓励特征重用
- 一定程度上减少了参数的数量