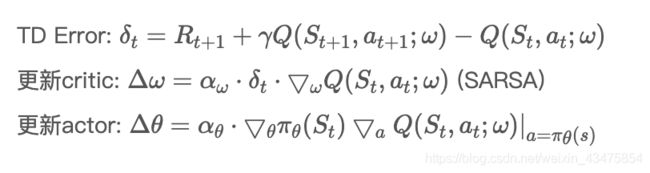强化学习教程（四）：从PDG到DDPG的原理及tf代码实现详解

强化学习教程（四）：从PDG到DDPG的原理及tf代码实现详解

原创 lrhao 公众号：ChallengeHub
收录于话题
#强化学习教程

前言

在前面强化学习教程（三）中介绍了基于策略「PG」算法，相比较DQN算法，PG是一种学习连续行为控制策略的方法，通过概率分布分布函数π，来表示每一步的最优策略，在每一步根据该概率分布进行action采样，获取当前最佳的action取值，即：

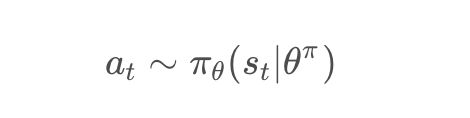
生成action的过程，本质是一个随机过程，最后学习到的策略，也是一个随机策略（stochastic polic）。

1.DPG
确定性策略梯度（Deterministic Policy Gradient，DPG），每一步的行为通过函数μ直接获得确定的值：
图片
这个函数μ即最优行为策略，不再是一个需要采样的随机策略。

我们在强化学习教程（三）中知道，策略梯度的损失函数就是负的最大化奖励函数，即策略梯度就是沿着使得目标函数变大的方向调整策略的参数，定义如下：

在上述公式中，我们能能够发现J函数主要与策略梯度和值函期望有关，因此为了解决策略和值函数之间的问题，采用一种新的思路将两个网络分开，即Actor-Critic网络。

1.1Actor-Critic
从命名中中可以显而易见知道这两个网络的工作流程：即
Actor(演员)-Critic(评论家)框架，相当于演员和评论家共同来提升表演，演员跳舞的姿态可能动作不到位，于是评论家告诉演员，你这样跳舞不好，它会建议演员修改一下舞姿了，当演员在某个舞姿上表演的比较好，那评论家就会告诉演员, 不错，你可以加大力度往这个方向发展，是不是明白其中的意思了？

在Actor-Critic（AC）框架中：
使用acotr神经网络来近似策略函数，输入时obsseraction（obs），输出action（a）；
critic神经网络来近似值函数，输入是action和obs [a, s]，输出是Q(s, a)。

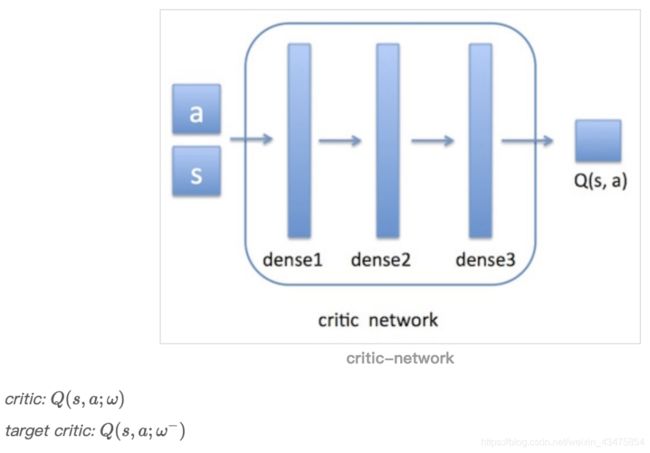
AC框架的流程：首先环境会给出一个obs，智能体根据actor网络（后面会讲到在此网络基础上增加噪声）做出决策action，环境收到此action后会给出一个奖励reward，及新的obs。这个过程是一个step。此时我们要根据reward去更新critic网络，然后沿critic建议的方向去更新actor网络。接着进入下一个step。如此循环下去，直到我们训练出了一个好的actor网络。

那么每次迭代如何更新这两个神经网络的参数呢？

与DQN一样，DDPG中也使用了target网络来保证参数的收敛：
假设critic网络为Q(s,a;ω)，他对应的target critic网络为
Q(s,a;ω−)。
actor网络为π(s;θ)，它对应的target actor网络为
π(s;θ−)。

1.1.1actor网络更新
actor网络用于参数化策略。这里涉及到之前说到的策略梯度Policy Gradient。

Tips：策略梯度这一块可以分为四种情况分别讨论：stochastic on-policy, stochastic off-policy, deterministic on-policy 和 deterministic off-policy，其实就是决定性策略和随机性策略，对应的在线学习和离线学习两辆组合。

确定性策略梯度定理提供了更新确定性策略的方法。将此方法用到Actor-Critic算法中：
(1) On-Policy Deterministic Actor-Critic

由于使用的是Sarsa（是一种在线学习算法）更新critic，因此是一种在线的确定性AC策略

(2) Off-Policy Deterministic Actor-Critic
由于使用的是Q-Learning更新critic，因此是一种离线的确定性AC策略

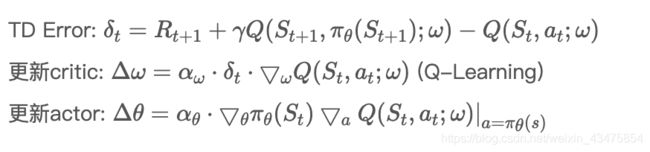
1.1.2critic网络更新
critic网络用于值函数近似，更新方式与DQN中的类似：

然后使用梯度下降法进行更新。

注意：actor和critic都使用了target网络来计算target。

2.DDPG

深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）是将深度学习神经网络融合进DPG的策略学习方法，相比较DPG核心改进地方在于：
采用卷积神经网络作为策略函数μ和Q函数的模拟，即策略网络和Q网络；然后使用深度学习的方法来训练上述神经网络。
在DQN中使用单个Q神经网络算法，学习过程很不稳定，
因为Q网络的参数在频繁gradient update的同时，又用于计算Q网络和策略网络的gradient：

在训练完一个mini-batch的数据之后，通过SGA/SGD算法更新online网络的参数，然后再通过soft update算法更新 target 网络的参数。soft update是一种running average的算法：

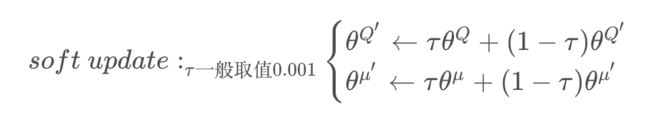
优点：target网络参数变化小，用于在训练过程中计算online网络的gradient，比较稳定，训练易于收敛。
代价：参数变化小，学习过程变慢。

DDPG核心思想

采用经验回放方法
采用target目标网络更新，不过DQN中的target更新是hard update，即每隔固定步数更新一次target网络，DDPG使用soft update，每一步都会更新target网络，只不过更新的幅度非常小
AC框架
确定性策略梯度

DDPG算法流程

初始化actor-critic神经网络thea_Q、thea_u
将online网络参数拷贝给对应target网络
初始化replay memory buffer R；
for each episode：
初始化UO随机过程；
for t = 1，T：
下面的步骤与DDPG算法实现框架图中步骤编号对应：

DDPG实现框架：

总结一下：
actor-critic框架是一个在循环的episode和时间步骤条件下，通过环境、actor和critic三者交互，来迭代训练策略网络、Q网络的过程。

DDPG对于DPG的关键改进

• 使用卷积神经网络来模拟策略函数和Q函数，并用深度学习的方法来训练，证明了在RL方法中，非线性模拟函数的准确性和高性能、可收敛；
• 而DPG中，可以看成使用线性回归的机器学习方法：使用带参数的线性函数来模拟策略函数和Q函数，然后使用线性回归的方法进行训练。
• experience replay memory的使用：actor同环境交互时，产生的transition数据序列是在时间上高度关联(correlated)的，如果这些数据序列直接用于训练，会导致神经网络的overfit，不易收敛。
• DDPG的actor将transition数据先存入experience replay buffer, 然后在训练时，从experience replay buffer中随机采样mini-batch数据，这样采样得到的数据可以认为是无关联的。
• target 网络和online 网络的使用， 使的学习过程更加稳定，收敛更有保障。

DDPG算法应用

下面展示DDPG算法将杆子立起来的一个应用

  1import tensorflow as tf
  2import numpy as np
  3import gym
  4import time
  5
  6# 定义超参数
  7MAX_EPISODES = 200
  8MAX_EP_STEPS = 200
  9LR_A = 0.001    # actor学习率
 10LR_C = 0.002    # critic学习率
 11GAMMA = 0.9     # 累计折扣奖励因子
 12TAU = 0.01      # 软更新tao
 13MEMORY_CAPACITY = 10000  # buffer R, 经验回放容器
 14BATCH_SIZE = 32  # 每批随机读取批次大小
 15
 16RENDER = False
 17ENV_NAME = 'Pendulum-v0'
 18
 19# 定义DDPG类
 20class DDPG(object):
 21    def __init__(self, a_dim, s_dim, a_bound,):
 22        # memory 存放的是序列（s,a,r,s+1）= s*2+a+1(r=1)
 23        self.memory = np.zeros((MEMORY_CAPACITY, s_dim * 2 + a_dim + 1), dtype=np.float32)
 24        self.pointer = 0
 25        self.sess = tf.Session()
 26
 27        self.a_dim, self.s_dim, self.a_bound = a_dim, s_dim, a_bound,
 28        self.S = tf.placeholder(tf.float32, [None, s_dim], 's')
 29        self.S_ = tf.placeholder(tf.float32, [None, s_dim], 's_')
 30        self.R = tf.placeholder(tf.float32, [None, 1], 'r')
 31
 32        # 建立网络，actor网络输入是S,critic输入是s,a
 33        self.a = self._build_a(self.S,)
 34        q = self._build_c(self.S, self.a, )
 35
 36        a_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Actor')
 37        c_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Critic')
 38        # soft updating
 39        """
 40        tf.train.ExponentialMovingAverage(decay)是采用滑动平均的方法更新参数。这个函数初始化需要提供一个衰减速率（decay），用于控制模型的更新速度。这个函数还会维护一个影子变量（也就是更新参数后的参数值），这个影子变量的初始值就是这个变量的初始值，影子变量值的更新方式如下：
 41   shadow_variable = decay * shadow_variable + (1-decay) * variable
 42   shadow_variable是影子变量，variable表示待更新的变量，也就是变量被赋予的值，decay为衰减速率。decay一般设为接近于1的数（0.99,0.999）。decay越大模型越稳定，因为decay越大，参数更新的速度就越慢，趋于稳定。
 43        """
 44
 45        ema = tf.train.ExponentialMovingAverage(decay=1 - TAU)          # soft replacement
 46        def ema_getter(getter, name, *args, **kwargs):
 47            return ema.average(getter(name, *args, **kwargs))
 48
 49        target_update = [ema.apply(a_params), ema.apply(c_params)]      # soft update operation
 50        a_ = self._build_a(self.S_, reuse=True, custom_getter=ema_getter)   # replaced target parameters
 51        q_ = self._build_c(self.S_, a_, reuse=True, custom_getter=ema_getter)
 52
 53        a_loss = - tf.reduce_mean(q)  # maximize the q
 54        self.atrain = tf.train.AdamOptimizer(LR_A).minimize(a_loss, var_list=a_params)
 55
 56        with tf.control_dependencies(target_update):    # soft replacement happened at here
 57            q_target = self.R + GAMMA * q_
 58            td_error = tf.losses.mean_squared_error(labels=q_target, predictions=q)
 59            self.ctrain = tf.train.AdamOptimizer(LR_C).minimize(td_error, var_list=c_params)
 60
 61        self.sess.run(tf.global_variables_initializer())
 62
 63    # 选取动作函数
 64    def choose_action(self, s):
 65        return self.sess.run(self.a, {self.S: s[np.newaxis, :]})[0]
 66
 67    # 从R buffer中学习
 68    def learn(self):
 69        indices = np.random.choice(MEMORY_CAPACITY, size=BATCH_SIZE)
 70        bt = self.memory[indices, :]
 71        bs = bt[:, :self.s_dim]
 72        ba = bt[:, self.s_dim: self.s_dim + self.a_dim]
 73        br = bt[:, -self.s_dim - 1: -self.s_dim]
 74        bs_ = bt[:, -self.s_dim:]
 75
 76        self.sess.run(self.atrain, {self.S: bs})
 77        self.sess.run(self.ctrain, {self.S: bs, self.a: ba, self.R: br, self.S_: bs_})
 78
 79    # 存储序列
 80    def store_transition(self, s, a, r, s_):
 81        transition = np.hstack((s, a, [r], s_))
 82        index = self.pointer % MEMORY_CAPACITY  # replace the old memory with new memory
 83        self.memory[index, :] = transition
 84        self.pointer += 1
 85
 86    # 建立actor网络（输入S_dim，输出a_dim, 采用tanh激活函数）
 87    def _build_a(self, s, reuse=None, custom_getter=None):
 88        trainable = True if reuse is None else False
 89        with tf.variable_scope('Actor', reuse=reuse, custom_getter=custom_getter):
 90            net = tf.layers.dense(s, 30, activation=tf.nn.relu, name='l1', trainable=trainable)
 91            a = tf.layers.dense(net, self.a_dim, activation=tf.nn.tanh, name='a', trainable=trainable)
 92            return tf.multiply(a, self.a_bound, name='scaled_a')
 93
 94    # 建立critic网络（输入S_dim，s_dim, 输出q）
 95    def _build_c(self, s, a, reuse=None, custom_getter=None):
 96        trainable = True if reuse is None else False
 97        with tf.variable_scope('Critic', reuse=reuse, custom_getter=custom_getter):
 98            n_l1 = 30
 99            w1_s = tf.get_variable('w1_s', [self.s_dim, n_l1], trainable=trainable)
100            w1_a = tf.get_variable('w1_a', [self.a_dim, n_l1], trainable=trainable)
101            b1 = tf.get_variable('b1', [1, n_l1], trainable=trainable)
102            net = tf.nn.relu(tf.matmul(s, w1_s) + tf.matmul(a, w1_a) + b1)
103            return tf.layers.dense(net, 1, trainable=trainable)  # Q(s,a)
104
105
106# training process
107
108# 环境初始化
109env = gym.make(ENV_NAME)
110env = env.unwrapped
111env.seed(1)
112
113# 获取s,a的维度
114s_dim = env.observation_space.shape[0]
115a_dim = env.action_space.shape[0]
116a_bound = env.action_space.high
117
118ddpg = DDPG(a_dim, s_dim, a_bound)
119
120var = 3  # 定义探索因子
121
122t1 = time.time()
123for i in range(MAX_EPISODES):
124    s = env.reset()
125    ep_reward = 0
126    for j in range(MAX_EP_STEPS):
127        if RENDER:
128            env.render()
129
130        # 添加探索噪音
131        a = ddpg.choose_action(s)
132        a = np.clip(np.random.normal(a, var), -2, 2)    # 随机选取动作探索
133        # np.clip()函数是，如果随机生成的数字大于2，则为2 ，如果小于-2，则为-2，其他则为本身
134
135        s_, r, done, info = env.step(a)
136        ddpg.store_transition(s, a, r / 10, s_)
137
138        if ddpg.pointer > MEMORY_CAPACITY:
139            var *= .9995    # 减缓动作探索度，即衰减速率
140            ddpg.learn()
141
142        s = s_
143        ep_reward += r
144        if j == MAX_EP_STEPS-1:
145            print('Episode:', i, ' Reward: %i' % int(ep_reward), 'Explore: %.2f' % var, )
146            # if ep_reward > -300:RENDER = True
147            break
148
149print('Running time: ', time.time() - t1)

参考资料

• https://blog.csdn.net/gsww404/article/details/80403150
• https://blog.csdn.net/kenneth_yu/article/details/78478356
• https://wanjun0511.github.io/2017/11/19/DDPG/

END

欢迎加入学习交流群

添加助手微信，可加入微信交流群