蒟蒻君的数学学习之路1：斐波那契数列的n种解法

⭐前言

fib数列相信大家都已经肥肠熟悉啦~
原问题是这样滴：

---

农场里有一堆兔几，兔几分为两类：大兔几和小兔几。
最开始（第一个月）有一只小兔几。
之后每过一个月：

• 上一个月的小兔几都会长大成大兔几，
• 上个月的每只大兔几会生一只小兔几（假设所有兔几都是母的qwq）。

农场主想知道，第n个月有多少只兔几（兔几会长生不老术，不会卒）。

---

月份	大兔几数	小兔几数	总数
1️⃣	$0$	$1$	$1$
2️⃣	$1$	$0$	$1$
3️⃣	$1$	$1$	$2$
4️⃣	$2$	$1$	$3$
5️⃣	$3$	$2$	$5$
6️⃣	$5$	$3$	$8$
7️⃣	$8$	$5$	$13$
…

这道问题其实比较简单，但是其实这里也是有很多解法滴~
下面由蒟蒻君来和大家一起 让简单的问题变复杂 学习这个问题的n种解法。

⭐一、 递推

$1$.$1$ 思路

观察上表可知：

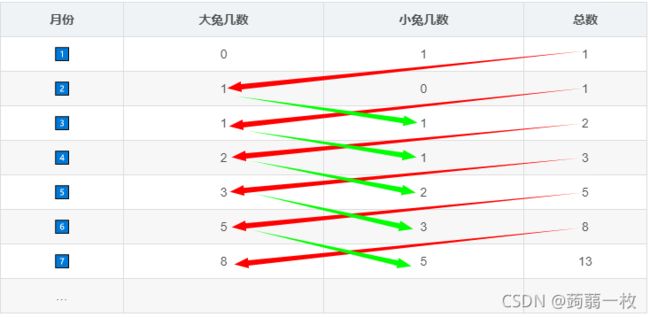
即第$i$个月的大兔几个数为第$i-1$个月的兔几总数，小兔几数为第$i-1$个月的大兔几数。
问题结束
下面蒟蒻君来为大家分析一下：

• 第$i$个月的大兔几包括第$i-1$个月的大兔几（不变）和第$i-1$个月的小兔几（长大），即第$i-1$个月的兔几总数；
• 第$i$个月的小兔几都是第$i-1$个月的大兔几生的（一个大兔几生一个小兔几），即和第$i-1$个月的大兔几总数相等。而根据上一条结论， 第$i$个月的小兔几数就是第$i-2$个月的兔几总数。
  我们设f[i]为第$i$个月的兔几总数：
• 对于$i<=2$，$f[i]=1$；
• 对于$i>2$，$f[i]=f[i-1]+f[i-2]$。

$1.2$ 优化：滚动数组

我们会发现，$f[i]$的值仅仅和$f[i-1]$和$f[i-2]$有关，即前面的值都没用了。
那么我们可以把$f$数组简化成三个变量：
$a$表示$f[i-2]$，$b$表示$f[i-1]$，c表示$f[i]$。

$1.3$ 效率分析

直接递推
时间复杂度：$O(n)$；
空间复杂度：$O(n)$。
滚动数组优化
时间复杂度：$O(n)$；
空间复杂度：$O(1)$。

比较费时间。

$1.4$ 代码

直接递推

#include 
using namespace std;
int f[105];
int main() {
     
	int n;
	cin >> n;
	f[1] = f[2] = 1;
	for (int i = 3; i <= n; ++i) {
     
		f[i] = f[i - 1] + f[i - 2];
	}
	cout << f[n] << '\n';
	return 0;
}

滚动数组优化

#include 
using namespace std;
int main() {
     
	int n;
	cin >> n;
	// 注意特判 
	if (n <= 2) {
     
		cout << 1 << '\n';
		return 0;
	}
	int a = 1, b = 1, c;
	for (int i = 3; i <= n; ++i) {
     
		c = a + b;
		a = b;
		b = c;
	}
	cout << c << '\n';
	return 0;
}

⭐二、递归

$2.1$ 思路

和递推的思路相似，唯一不同的就是递推是自底向上推到，递归是从上往下推。

$2.2$ 优化：记忆化搜索

如果直接递归的话，其实时间复杂度是比较高的。比如我们调用$f(5)$时就会有如下搜索路径（过程见代码）：

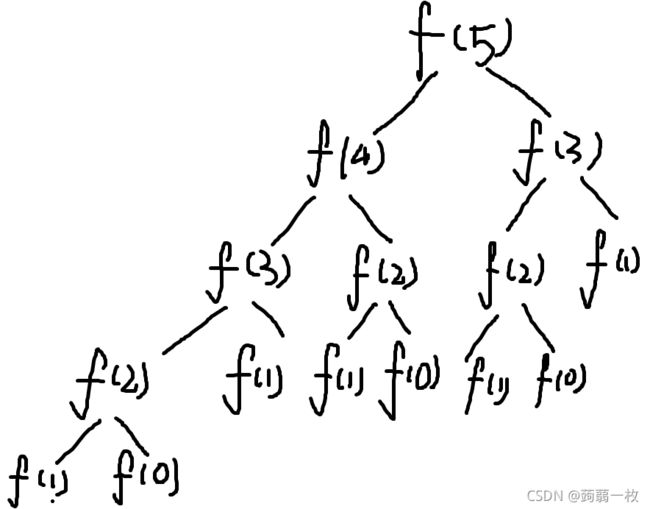
我们会发现这种复杂度与递推的线性复杂度相差甚远，因为这里出现的多次搜索同一个结点的问题，导致复杂度飙升。
我们可以用一个数组$a$记录之前搜索过的结点，这样就减少了很多不必要的搜索。

$2.3$ 效率分析

直接递归
时间复杂度：$O(2^n)$ （n层二叉树最多有$2^{n-1}-1$个结点，忽略常数项）；
空间复杂度：$O(n)$ （即树的高度）。
记忆化搜索优化
时间复杂度：$O(n)$；
空间复杂度：$O(n)$。

比较费时间。

$2.4$ 代码

直接递归

#include 
using namespace std;
int f(int n) {
     
	if (n == 1 || n == 2) {
     
		return 1;
	}
	return f(n - 1) + f(n - 2);
}
int main() {
     
	int n;
	cin >> n;
	cout << f(n) << '\n';
	return 0;
}

记忆化搜索优化

#include 
using namespace std;
int a[105];
int f(int n) {
     
	// 如果搜索过就直接返回，剪掉这个子树 
	if (a[n] != 0) {
     
		return a[n];
	}
	if (n == 1 || n == 2) {
     
		return 1;
	}
	return f(n - 1) + f(n - 2);
}
int main() {
     
	int n;
	cin >> n;
	cout << f(n) << '\n';
	return 0;
}

⭐三、矩阵快速幂

$3.1$ 思路

众所周知，矩阵快速幂很适合解决线性dp。

• 我们构造表示最后答案的矩阵。
• 比如我们可以先构造一个$1\times 2$的矩阵$a$，里面填$f[1]$和$f[2]$。
• 接下来我们就需要构造一个使得$b$，使得$a\times b=[f[2],f[3]]$
• 我们依次判断后面矩阵的每一项，看它可以被前面的哪一项凑出来。
  例如前面的$f[2](b)=f[2](a)，f[3](b)=f[1](a)+f[2](a)$，所以此时我们应该构造$2\times 2$的矩阵$\begin{array}{cc}0& 1\\ 1& 1\end{array}$。
• 重复以上步骤…

$3.2$ 效率分析

时间复杂度：$O(logn)$；
空间复杂度：$O(n^2)$。

比较费空间。

$3.3$ 代码

#include 
using namespace std;
struct matrix {
     
   int a[105][105];
};
const int N = 2;
matrix mul(matrix A, matrix B, bool flag = false) {
     
    matrix res;
    for (int i = 1; i <= N; ++i) {
     
        for (int j = 1; j <= N; ++j) {
     
            res.a[i][j] = 0;
            for (int k = 1; k <= N - flag; ++k) {
     
                res.a[i][j] += A.a[i][k] * B.a[k][j];
            }
        }
    }
    return res;
}
matrix unit() {
     
    matrix res;
    for (int i = 1; i <= N; ++i) {
     
        for (int j = 1; j <= N; ++j) {
     
            if (i == j) {
     
                res.a[i][j] = 1;
            } else {
     
                res.a[i][j] = 0;
            }
        }
    }
    return res;
}
matrix pow(matrix A, int n) {
     
    matrix res = unit();
    while (n) {
     
        if (n & 1) {
     
            res = mul(res, A);
        }
        A = mul(A, A);
        n >>= 1;
    }
    return res;
}
int f(int n) {
     
    matrix A;
    A.a[1][1] = A.a[1][2] = A.a[2][1] = 1;
    A.a[2][2] = 0;
    A = pow(A, n - 1);
    matrix res;
    res.a[1][1] = res.a[2][1] = 1;
    res = mul(res, A, true);
    return res.a[2][1];
}
int main() {
     
    int n;
    cin >> n;
    cout << f(n) << '\n';
    return 0;
}

⭐四、通项公式

$4.1$ 公式及证明：待定系数法

最优解来了。

我们用待定系数法推到斐波那契数列的通项公式（自己推的可能有点复杂QWQ）。

1. 我们先假设斐波那契数列是一个等比数列 $\left\{x^n\right\}$，$x\ne 0$，$x^1=1$。
2. 则根据斐波那契数列递推式可得：$x^{n-2}+x^{n-1}=x^n$。
   提出$x^n$可得 $\left(x^2-x-1\right)x^n=0$。$x^n\ne 0$，则$x^2-x-1=0$。
   解得两个实根$x=\frac{1\pm \sqrt{5}}{2}$。
3. 使用待定系数法，设出 $a,b$ 使得：
   $\{\begin{array}{l}a\left(\frac{1+\sqrt{5}}{2}\right)+b\left(\frac{1-\sqrt{5}}{2}\right)=1\\ a{\left(\frac{1+\sqrt{5}}{2}\right)}^2+b{\left(\frac{1-\sqrt{5}}{2}\right)}^2=1\end{array}$
   解得$a=\frac{1}{\sqrt{5}},b=-\frac{1}{\sqrt{5}}$。
4. 最后推出通项公式：$f(n)=\frac{{\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n}{\sqrt{5}}$。

$4.2$ 效率分析

时间复杂度：$O(1)$；
空间复杂度：$O(1)$。
perfect

$4.3$ 代码

#include 
using namespace std;
int main() {
     
	ios :: sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int n;
	cin >> n;
	double t = sqrt(5);
	cout << (pow((1 + t) / 2, n) - pow((1 - t) / 2, n)) / t << '\n';
	return 0;
}

古德拜，大家下期再见~
传送门（暂空）