大厂算法面试之leetcode精讲11剪枝&回溯
视频讲解(高效学习):点击学习
目录:
剪枝
排除那些不符合条件的分支。提高程序的运行效率。
回溯:
一层层递归,尝试搜素答案,
- 找到答案:返回结果,尝试其他的分支
- 找不到答案:返回上一层,尝试其他分支
回溯模版:
result = [];
function backtrack (path, list) {
if (满足条件) {
result.push(path);
return
}
for () {
// 单层逻辑
backtrack (path, list)
// 撤销选择 重置状态
}
}回溯四部曲:
- 回溯参数
- 终止条件
- 单层递归逻辑
- 选择其他分支(撤销选择 重置状态)
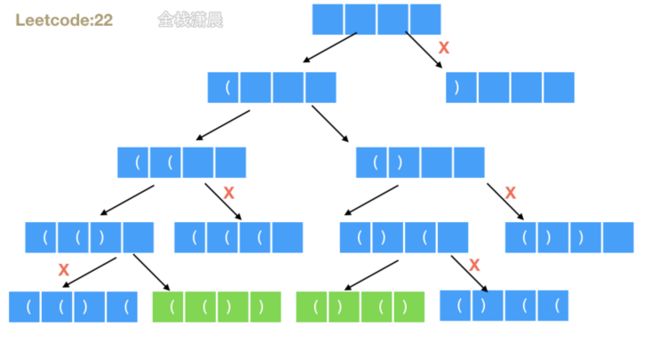
22. 括号生成 (medium)
方法1:暴力
复杂度分析:时间复杂度O(2^2n*n),字符串的长度为2n,每个位置有两种选择,选择左或者右括号,验证字符串是否有效复杂度O(n),剪枝之后会优化,最坏的情况是O(2^2n*n)。空间复杂度O(n),递归次数最多2n
方法2.递归dfs
- 思路:采用递归,终止条件是字符串的长度等于
2n,递归函数传入构建的字符串,左右括号剩余多少,每个位置有两种选择,选择左或者右括号,这里可以进行剪枝优化,只有右括号的保有数量大于左括号的保有数量,才能选右括号,否则肯定不能构成有效括号
Js:
const generateParenthesis = (n) => {
const res = []; // 输出的结果数组
const generate = (str, left, right) => {
if (str.length == 2 * n) { // 字符串构建完成
res.push(str); // 将字符串加入res
return; // 结束当前递归(结束当前搜索分支)
}
if (left > 0) { // 只要左括号有剩,可以选它,继续递归做选择
generate(str + '(', left - 1, right);
}
if (right > left) { // 右括号的保有数量大于左括号的保有数量,才能选右括号
generate(str + ')', left, right - 1);
}
};
generate('', n, n); // 递归的入口,初始字符串是空字符串,初始括号数量都是n
return res;
};Java:
class Solution {
List res = new ArrayList<>();
public List generateParenthesis(int n) {
generate(n, n, "");
return res;
}
private void generate(int left, int right, String curStr) {
if (left == 0 && right == 0) {
res.add(curStr);
return;
}
if (left > 0) {
generate(left - 1, right, curStr + "(");
}
if (right > left) {
generate(left, right - 1, curStr + ")");
}
}
} 方法3.回溯
- 思路:当左括号剩下的多,说明字符串中的左括号数量少于右括号,不合法,对字符串尝试添加左括号,然后回溯,尝试添加右括号,然后尝试回溯
Js:
var generateParenthesis = function(n) {
if (n == 0) return []
const res = []
let track = []
backtrack(n, n, track, res)
return res
function backtrack(left, right, track, res) {
// 数量小于0,不合法
if (left < 0 || right < 0) return
// 若左括号剩下的多,说明不合法
if (right < left) return
// 所有括号用完,得到合法组合
if (left == 0 && right == 0) {
res.push(track.join(''))
return
}
// 尝试添加左括号
track.push('(')
//这个地方一定要注意 需要拷贝一份track,也就是采用[...track], 不然会影响其他分支
backtrack(left - 1, right, [...track], res)
track.pop()
// 尝试添加右括号
track.push(')')
backtrack(left, right - 1, [...track], res)
track.pop()
}
};
Java:
class Solution {
public List generateParenthesis(int n) {
List res = new ArrayList();
backtrack(res, new StringBuilder(), 0, 0, n);
return res;
}
public void backtrack(List res, StringBuilder cur, int left, int right, int max) {
if (cur.length() == max * 2) {
res.add(cur.toString());
return;
}
if (left < max) {
cur.append('(');
backtrack(res, cur, left + 1, right, max);
cur.deleteCharAt(cur.length() - 1);
}
if (right < left) {
cur.append(')');
backtrack(res, cur, left, right + 1, max);
cur.deleteCharAt(cur.length() - 1);
}
}
}
51. N 皇后 (hard)
方法1.回溯
- 思路:从上到下,从左到右遍历棋盘,准备好三个set分别记录列和两个对角线可以攻击到的坐标,尝试在每个空位放置皇后,放置之后更新三个可以攻击到的set坐标,然后继续下一层遍历,完成下一层之后,尝试回溯当前层,也就是撤销当前层放置的皇后,同时撤销三个可以攻击到的set坐标,不断回溯,直到遍历完成,找到所有可能的解。
- 复杂度分析:时间复杂度:
O(N!),其中 N 是皇后数量,由于每个皇后必须位于不同列,因此已经放置的皇后所在的列不能放置别的皇后。第一个皇后有 N 列可以选择,第二个皇后最多有 N-1列可以选择...。空间复杂度:O(N),其中 N 是皇后数量,空间复杂度主要取决于递归调用层数、记录每行放置的皇后列下标的数组以及三个集合,递归调用层数不会超过 N,数组的长度为 N,每个集合的元素个数都不会超过 N。
js:
const solveNQueens = (n) => {
const board = new Array(n);
for (let i = 0; i < n; i++) {
board[i] = new Array(n).fill('.');//生成board
}
const cols = new Set(); // 列集,记录出现过皇后的列
const diag1 = new Set(); // 正对角线集
const diag2 = new Set(); // 反对角线集
const res = [];//结果数组
const backtrack = (row) => {
if (row == n) {//终止条件
const stringsBoard = board.slice();
for (let i = 0; i < n; i++) {//生成字符串
stringsBoard[i] = stringsBoard[i].join('');
}
res.push(stringsBoard);
return;
}
for (let col = 0; col < n; col++) {
// 如果当前点的所在的列,所在的对角线都没有皇后,即可选择,否则,跳过
if (!cols.has(col) && !diag1.has(row + col) && !diag2.has(row - col)) {
board[row][col] = 'Q'; // 放置皇后
cols.add(col); // 记录放了皇后的列
diag2.add(row - col); // 记录放了皇后的正对角线
diag1.add(row + col); // 记录放了皇后的负对角线
backtrack(row + 1);
board[row][col] = '.'; // 撤销该点的皇后
cols.delete(col); // 对应的记录也删一下
diag2.delete(row - col);
diag1.delete(row + col);
}
}
};
backtrack(0);
return res;
};java:
class Solution {
public List> solveNQueens(int n) {
List> res = new ArrayList>();
int[] queens = new int[n];
Arrays.fill(queens, -1);
Set cols = new HashSet();
Set diag1 = new HashSet();
Set diag2 = new HashSet();
backtrack(res, queens, n, 0, cols, diag1, diag2);
return res;
}
public void backtrack(List> res, int[] queens, int n, int row, Set cols, Set diag1, Set diag2) {
if (row == n) {
List board = generateBoard(queens, n);
res.add(board);
} else {
for (int i = 0; i < n; i++) {
if (cols.contains(i)) {
continue;
}
int diagonal1 = row - i;
if (diag1.contains(diagonal1)) {
continue;
}
int diagonal2 = row + i;
if (diag2.contains(diagonal2)) {
continue;
}
queens[row] = i;
cols.add(i);
diag1.add(diagonal1);
diag2.add(diagonal2);
backtrack(res, queens, n, row + 1, cols, diag1, diag2);
queens[row] = -1;
cols.remove(i);
diag1.remove(diagonal1);
diag2.remove(diagonal2);
}
}
}
public List generateBoard(int[] queens, int n) {
List board = new ArrayList();
for (int i = 0; i < n; i++) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[queens[i]] = 'Q';
board.add(new String(row));
}
return board;
}
} 52. N皇后 II(hard)
方法1.位运算
js:
var totalNQueens = function (n) {
if (n < 1) return
let count = 0;
dfs(n, 0, 0, 0, 0)
return count
//n:皇后的数量
//row:当前行
//cols:放置皇后的位置
//diag1:可以攻击的左倾斜对角线
//diag2:可以攻击的右倾斜对角线
function dfs(n, row, cols, diag1, diag2) {
if (row >= n) {//递归终止 统计解法
count += 1;
return
}
//~(cols | diag1 | diag2):攻击的位置合起来 取反之后,1的位置就是可以放置皇后的位置
//(1 << n) - 1:从右向左,大于n的位置都变成0
//(~(cols | diag1 | diag2)) & ((1 << n) - 1):从右向左,可以放置皇后的位置,大于n的位置都变成0
let bits = (~(cols | diag1 | diag2)) & ((1 << n) - 1)
while (bits) {
let p = bits & -bits//取到从右向左第一个1
bits = bits & (bits - 1)//去掉从右向左第一个1
//列和两个对角线合上不可以放置的二进制位
dfs(n, row + 1, cols | p, (diag1 | p) << 1, (diag2 | p) >>> 1)
}
}
};Java:
class Solution {
public int totalNQueens(int n) {
return dfs(n, 0, 0, 0, 0);
}
public int dfs(int n, int row, int clos, int diag1, int diag2) {
if (row == n) {
return 1;
} else {
int count = 0;
int bits = ((1 << n) - 1) & (~(clos | diag1 | diag2));
while (bits != 0) {
int position = bits & (-bits);
bits = bits & (bits - 1);
count += dfs(n, row + 1, clos | position, (diag1 | position) << 1, (diag2 | position) >> 1);
}
return count;
}
}
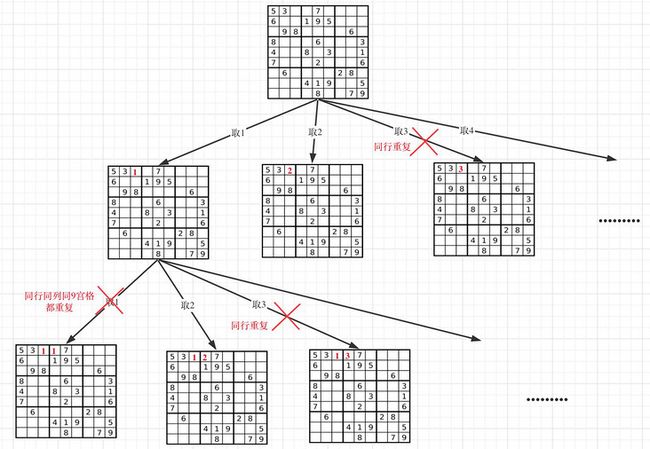
}36. 有效的数独 (medium)
方法1:回溯
- 思路:准备行、列、3 3小方块,三个哈希表或者set或者9 9的二维数组,都可以,只要能判重复即可,从上到下,从左到右循环,依次检查行、列、3 * 3小方块中是否有重复的数字,如果有则返回false,然后更新哈希表或者set。
- 复杂度分析:时间复杂度:
O(1),数独共有 81 个单元格,每个单元格遍历一次即可。空间复杂度:O(1),数独的大小固定,因此哈希表的空间也是固定的。
Js:
var isValidSudoku = function(board) {
// 方向判重
let rows = {};//行
let columns = {};//列
let boxes = {};//3*3小方块
// 遍历数独
for(let i = 0;i < 9;i++){
for(let j = 0;j < 9;j++){
let num = board[i][j];
if(num != '.'){//遇到有效的数字
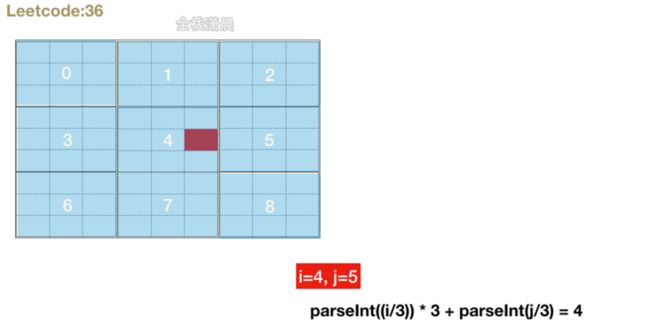
let boxIndex = parseInt((i/3)) * 3 + parseInt(j/3);// 子数独序号
if(rows[i+'-'+num] || columns[j+'-'+num] || boxes[boxIndex+'-'+num]){//重复检测
return false;
}
// 方向 + 数字 组成唯一键值,若出现第二次,即为重复
// 更新三个对象
rows[i+'-'+num] = true;
columns[j+'-'+num] = true;
boxes[boxIndex+'-'+num] = true;
}
}
}
return true;
};Java:
class Solution {
public boolean isValidSudoku(char[][] board) {
int[][] rows = new int[9][9];//用数组同样实现
int[][] columns = new int[9][9];
int[][][] boxes = new int[3][3][9];
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
char c = board[i][j];
if (c != '.') {
int index = c - '0' - 1;
rows[i][index]++;
columns[j][index]++;
boxes[i / 3][j / 3][index]++;
if (rows[i][index] > 1 || columns[j][index] > 1 || boxes[i / 3][j / 3][index] > 1) {
return false;
}
}
}
}
return true;
}
}37. 解数独(hard)
- 思路:循环行和列,尝试在每个位置放置1-9,并检验合法性,包括行、列、3 * 3方块的合法性,如果合法继续循环,直到找到一个合法的解,如果不合法,则回溯状态,并继续尝试其他的可能性
- 复杂度分析:同36题
js:
var solveSudoku = function(board) {
function isValid(row, col, val, board) {
let len = board.length
// 行中的数字不能重复
for(let i = 0; i < len; i++) {
if(board[row][i] === val) {
return false
}
}
// 列中的数字不能重复
for(let i = 0; i < len; i++) {
if(board[i][col] === val) {
return false
}
}
let startRow = Math.floor(row / 3) * 3
let startCol = Math.floor(col / 3) * 3
//方块中的数字不能重复
for(let i = startRow; i < startRow + 3; i++) {
for(let j = startCol; j < startCol + 3; j++) {
if(board[i][j] === val) {
return false
}
}
}
return true
}
function backTracking() {//回溯函数
for(let i = 0; i < board.length; i++) {
for(let j = 0; j < board[0].length; j++) {//循环行和列
if(board[i][j] !== '.') continue
for(let val = 1; val <= 9; val++) {//尝试在当前单元格放置1-9
if(isValid(i, j, `${val}`, board)) {//判断放置数字的合法性
board[i][j] = `${val}`//放置数字
if (backTracking()) {//合法返回ture
return true
}
board[i][j] = `.`//不合法回溯状态
}
}
return false//1-9的数字都不合法,返回false
}
}
return true//全部可能性都尝试完成 返回true 说明有解
}
backTracking()
return board
};Java:
class Solution {
public void solveSudoku(char[][] board) {
backTracking(board);
}
private boolean backTracking(char[][] board){
for (int i = 0; i < 9; i++){ // 遍历行
for (int j = 0; j < 9; j++){ // 遍历列
if (board[i][j] != '.'){
continue;
}
for (char k = '1'; k <= '9'; k++){ //尝试在当前位置放置1-9
if (isValid(i, j, k, board)){
board[i][j] = k;//放置数字
if (backTracking(board)){ //合法返回ture
return true;
}
board[i][j] = '.';
}
}
return false;//1-9的数字都不合法,返回false
}
}
return true;//全部可能性都尝试完成 返回true 说明有解
}
private boolean isValid(int row, int col, char val, char[][] board){
// 同行是否重复
for (int i = 0; i < 9; i++){
if (board[row][i] == val){
return false;
}
}
// 同列是否重复
for (int j = 0; j < 9; j++){
if (board[j][col] == val){
return false;
}
}
// 小方块中的元素是否重复
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++){
for (int j = startCol; j < startCol + 3; j++){
if (board[i][j] == val){
return false;
}
}
}
return true;
}
}
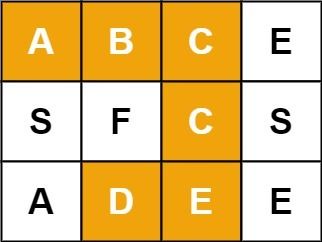
79. 单词搜索(medium)
思路:从上到下,左到右遍历网格,每个坐标递归调用
check(i, j, k)函数,i,j表示网格坐标,k表示word的第k个字符,如果能搜索到第k个字符返回true,否则返回false,check函数的终止条件有2种情况- 如果i,j位置的字符和字符串位置k的字符不相等,则这条搜索路径搜索失败 返回false
- 如果搜索到了字符串的结尾,则找到了网格中的一条路径,这条路径上的字符正好可以组成字符串s
两种情况都不满足则把当前网格节点加入
visited数组,visited表示节点已经访问过了,然后顺着当前网格坐标的四个方向继续尝试,如果没找到k开始的子串,则回溯状态visited[i] [j] = false,继续后面的尝试。- 复杂度分析:时间复杂度
O(MN⋅3^L),M,N 为网格的长度与宽度,L 为字符串 word 的长度,第一次调用check函数的时候,进行4个方向的检查,其余坐标的节点都是3个方向检查,走过来的分支不会反方向回去,所以check函数的时间复杂度是3^L,而网格有M*N个坐标,且存在剪枝,所以最坏的情况下时间复杂度是O(MN⋅3^L)。空间复杂度是O(MN),visited数组空间是O(MN),check递归栈的最大深度在最坏的情况下是O(MN)
方法1:回溯
Js:
var exist = function(board, word) {
const h = board.length, w = board[0].length;//网格的长和宽
const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];//方向数组
const visited = new Array(h);//标记是否访问过的数组
for (let i = 0; i < visited.length; ++i) {//初始化visited数组
visited[i] = new Array(w).fill(false);
}
const check = (i, j, s, k) => {//检查从网格i,j出发是否能搜索到0-k的字符组成的子串
//如果i,j位置的字符和第k个的字符不相等,则这条搜索路径搜索失败 返回false
if (board[i][j] != s.charAt(k)) {
return false;
//如果搜索到了字符串的结尾,则找到了网格中的一条路径,这条路径上的字符正好可以组成字符串s
} else if (k == s.length - 1) {
return true;
}
visited[i][j] = true;//标记i,j被访问过了
let result = false;
for (const [dx, dy] of directions) {//向i,j的四个方向继续尝试寻找
let newi = i + dx, newj = j + dy;
if (newi >= 0 && newi < h && newj >= 0 && newj < w) {//新的坐标位置合法检查
if (!visited[newi][newj]) {//新的坐标不能存在于visited中,也就是不能是访问过的
const flag = check(newi, newj, s, k + 1);//继续检查新的坐标
if (flag) {//如果在网格中找到了字符串 则跳过循环
result = true;
break;
}
}
}
}
visited[i][j] = false;//回溯状态
return result;//返回结果
}
for (let i = 0; i < h; i++) {
for (let j = 0; j < w; j++) {
const flag = check(i, j, word, 0);
if (flag) {
return true;
}
}
}
return false;
};
Java:
class Solution {
public boolean exist(char[][] board, String word) {
int h = board.length, w = board[0].length;
boolean[][] visited = new boolean[h][w];
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
boolean flag = check(board, visited, i, j, word, 0);
if (flag) {
return true;
}
}
}
return false;
}
public boolean check(char[][] board, boolean[][] visited, int i, int j, String s, int k) {
if (board[i][j] != s.charAt(k)) {
return false;
} else if (k == s.length() - 1) {
return true;
}
visited[i][j] = true;
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
boolean result = false;
for (int[] dir : directions) {
int newi = i + dir[0], newj = j + dir[1];
if (newi >= 0 && newi < board.length && newj >= 0 && newj < board[0].length) {
if (!visited[newi][newj]) {
boolean flag = check(board, visited, newi, newj, s, k + 1);
if (flag) {
result = true;
break;
}
}
}
}
visited[i][j] = false;
return result;
}
}
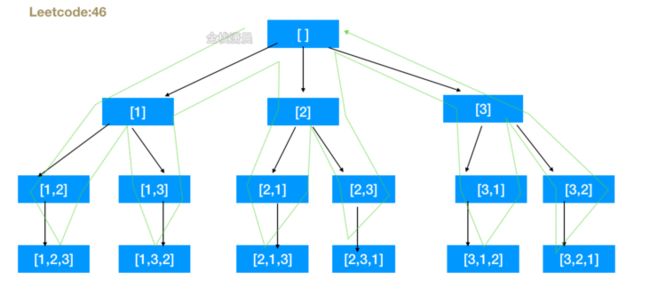
46. 全排列 (medium)
- 思路:准备path数组,存放每一个回溯递归的分支中的数字排列,调用回溯函数 传入nums,nums长度,used数组,used表示已经使用的数字,回溯函数中循环nums中的数,每层循环将nums中的元素加入path中,然后递归调用回溯函数,调用完成之后,回溯之前的状态,当path数组的长度和nums的长度相同就找到了一种排列。
- 复杂度:时间复杂度
O(n*n!)。空间复杂度O(n),递归栈深度
js:
var permute = function(nums) {
const res = [], path = [];
backtracking(nums, nums.length, []);//调用回溯函数 传入nums,nums长度,used数组
return res;
function backtracking(n, k, used) {
if(path.length === k) {//递归终止条件
res.push(Array.from(path));
return;
}
for (let i = 0; i < k; i++ ) {
if(used[i]) continue;//已经使用过了就跳过本轮循环
path.push(n[i]);
used[i] = true;
backtracking(n, k, used);//递归
path.pop();//回溯 将push进的元素pop出来 然后标记成未使用 继续其他分支
used[i] = false;
}
}
};
java:
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
boolean[] used;
public List> permute(int[] nums) {
if (nums.length == 0){
return result;
}
used = new boolean[nums.length];
permuteHelper(nums);
return result;
}
private void permuteHelper(int[] nums){
if (path.size() == nums.length){
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++){
if (used[i]){
continue;
}
used[i] = true;
path.add(nums[i]);
permuteHelper(nums);
path.removeLast();
used[i] = false;
}
}
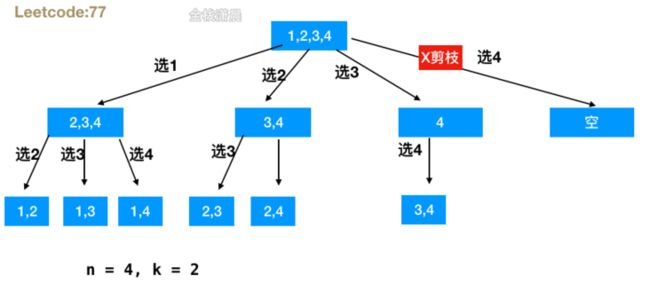
} 77. 组合 (medium)
- 思路:回溯函数传入n,k和选择的元素位置startIndex,在每层递归中,从startIndex开始循环到
n - (k - path.length) + 1的位置,将这些数加入path,然后startIndex加1,继续递归函数进入下一个分支,完成调用之后回溯状态,当path的长度等于k的时候终止这层分支,加入结果中。 - 复杂度:时间复杂度:
O(C(n, k) * k),枚举结果总数为C(n, k),每次得到一个结果需要O(k)时间。空间复杂度:O(n),最大是n层递归栈。
js:
const combine = (n, k) => {
const res = [];
const helper = (startIndex, path) => { //startIndex表示搜索的起点位置 path是每条分支的一个组合)
if (path.length == k) {
res.push(path.slice()); //需要拷贝一份 避免受其他分支的影响
return;
}
for (let i = startIndex; i <= n - (k - path.length) + 1; i++) {//剪枝
path.push(i); //加入path
helper(i + 1, path); //下一层递归
path.pop(); //回溯状态
}
};
helper(1, []); //递归入口
return res;
}
java:
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
public List> combine(int n, int k) {
combineHelper(n, k, 1);
return result;
}
private void combineHelper(int n, int k, int startIndex){
if (path.size() == k){
result.add(new ArrayList<>(path));
return;
}
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
path.add(i);
combineHelper(n, k, i + 1);
path.removeLast();
}
}
}
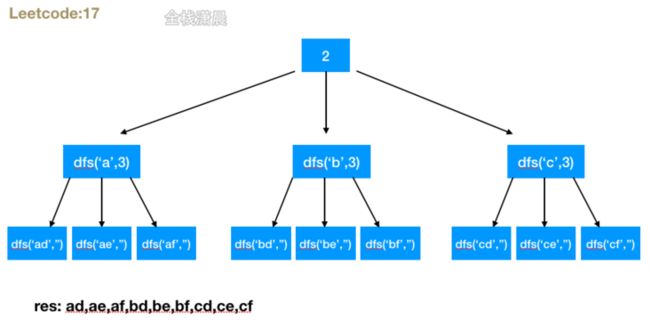
17. 电话号码的字母组合 (medium)
方法1.dfs+回溯
- 思路:深度优先遍历,遍历函数传入每一层形成的字符串和一个指向字符的位置指针,打给你指针的位置到达字符串的结尾时,将形成的字符串加入结果数组,递归的每一层遍历这一层的数字对应的字符,然后传入新的字符,指针向后移动一次,不断递归
- 复杂度:时间复杂度
O(3^m * 4^n),m,n分别是三个字母和四个字母对应的数字个数。空间复杂度O(m+n),递归栈的深度,最大为m+n
js:
//输入:digits = "23"
//输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
var letterCombinations = (digits) => {
if (digits.length == 0) return [];
const res = [];
const map = {//建立电话号码和字母的映射关系
2: "abc",
3: "def",
4: "ghi",
5: "jkl",
6: "mno",
7: "pqrs",
8: "tuv",
9: "wxyz",
};
const dfs = (curStr, i) => {//curStr是递归每一层的字符串,i是扫描的指针
if (i > digits.length - 1) {//边界条件,递归的出口
res.push(curStr); //其中一个分支的解推入res
return; //结束递归分支,进入另一个分支
}
const letters = map[digits[i]]; //取出数字对应的字母
for (const l of letters) {
//进入不同字母的分支
dfs(curStr + l, i + 1); //参数传入新的字符串,i右移,继续递归
}
};
dfs("", 0); // 递归入口,传入空字符串,i初始为0的位置
return res;
};java:
class Solution {
String[] map = { " ", "*", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
public List letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return new ArrayList<>();
}
dfs(digits, new StringBuilder(), 0);
return res;
}
List res = new ArrayList<>();
void dfs(String digits, StringBuilder curStr, int index) {
if (index == digits.length()) {
res.add(curStr.toString());
return;
}
char c = digits.charAt(index);
int pos = c - '0';
String map_string = map[pos];
for (int i = 0; i < map_string.length(); i++) {
curStr.append(map_string.charAt(i));
dfs(digits, curStr, index + 1);
curStr.deleteCharAt(curStr.length() - 1);
}
}
}
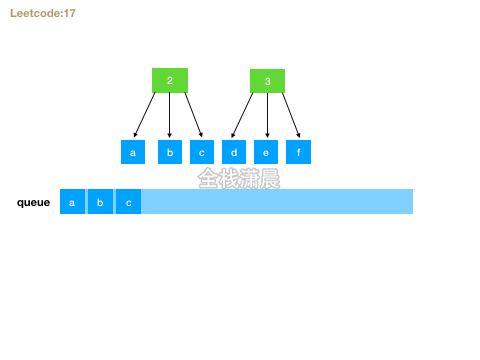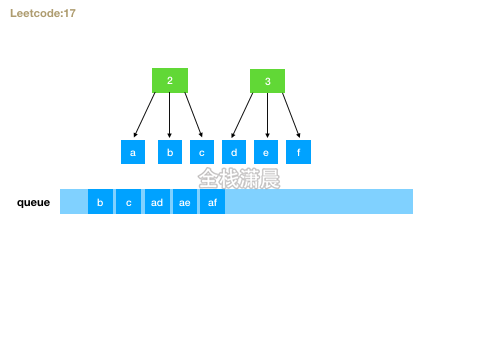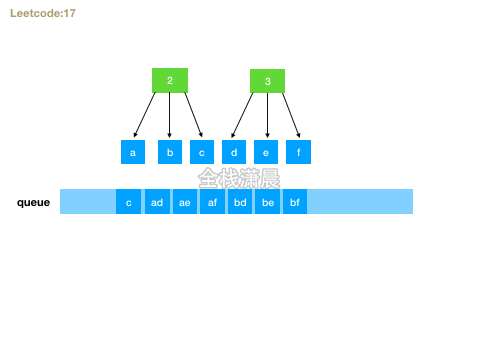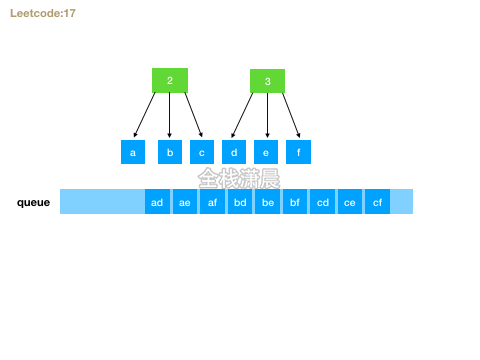
方法2.bfs
- 思路:用队列广度优先遍历,先循环数字数组,然后取出对应的字母,与当前层的字符串组成新的字符串加入队列,遍历完成之后,队列的最后一层就是解。
- 复杂度:时间复杂度
O(3^m * 4^n),m,n分别是三个字符和四个字母对应的数组个数。空间复杂度O(3^m * 4^n),队列的空间大小,最大为3^m * 4^n
js:
var letterCombinations = (digits) => {
if (digits.length == 0) return [];
const map = {
2: "abc",
3: "def",
4: "ghi",
5: "jkl",
6: "mno",
7: "pqrs",
8: "tuv",
9: "wxyz",
};
const queue = [];
queue.push("");
for (let i = 0; i < digits.length; i++) {//循环数字的每个字符
const levelSize = queue.length; //当前层的节点个数
for (let j = 0; j < levelSize; j++) {
const curStr = queue.shift(); //当前层的字符串
const letters = map[digits[i]];//获取数字对应的字母字符
for (const l of letters) {
queue.push(curStr + l); //新生成的字符串入列
}
}
}
return queue; //最后一层生成的字符串就是解
};java:
class Solution {
public List letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return new ArrayList();
}
String[] map = { " ", "*", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
List res = new ArrayList<>();
res.add("");
for (int i = 0; i < digits.length(); i++) {
String letters = map[digits.charAt(i) - '0'];
int levelSize = res.size();
for (int j = 0; j < levelSize; j++) {
String tmp = res.remove(0);
for (int k = 0; k < letters.length(); k++) {
res.add(tmp + letters.charAt(k));
}
}
}
return res;
}
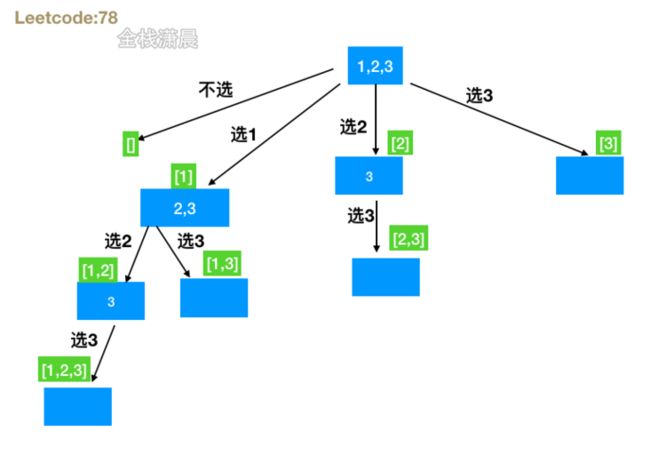
} 78. 子集 (medium)
- 思路:回溯函数传入字符开始的位置startIndex,不断递归,每一层startIndex加1,当一个分支结束之后在,开始回溯,进入另一个分支。
- 复杂度:时间复杂度
O(n*2^n),如图递归出来的状态是2^n个状态,每个状态构建path数组复杂度是O(n)。空间复杂度O(n),也就是递归栈的空间
js:
//例子:nums = [1,2,3]
var subsets = function(nums) {
let result = []//存放结果
let path = []//存放一个分支的结果
function backtracking(startIndex) {//startIndex字符递归开始的位置
result.push(path.slice())//path.slice()断开和path的引用关系
for(let i = startIndex; i < nums.length; i++) {//从startIndex开始递归
path.push(nums[i])//当前字符推入path
backtracking(i + 1)//startIndex向后移动一个位置 继续递归
path.pop()//回溯状态
}
}
backtracking(0)
return result
};
java:
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
public List> subsets(int[] nums) {
if (nums.length == 0){
result.add(new ArrayList<>());
return result;
}
backtracking(nums, 0);
return result;
}
private void backtracking(int[] nums, int startIndex){
result.add(new ArrayList<>(path));
if (startIndex >= nums.length){
return;
}
for (int i = startIndex; i < nums.length; i++){
path.add(nums[i]);
backtracking(nums, i + 1);
path.removeLast();
}
}
}
473. 火柴拼正方形 (medium)
- 思路 :排序nums数组,减少回溯的次数。不断尝试将nums中的元素放入4个桶中,如果都能放的下,则能拼成正方形
js:
//例子:[1,2,2,2,1]
var makesquare = function (nums) {
function backtrack(i, nums, edge, bucket) {
if (i >= nums.length) {//递归结束条件
return true;
}
for (let j = 0; j < 4; j++) {//循环4个桶
if (bucket[j] + nums[i] > edge) {//这个桶装不下 继续找下一个桶
continue;
}
bucket[j] += nums[i];//将当前元素加入桶中
if (backtrack(i + 1, nums, edge, bucket)) {//索引i加1 继续递归下一个nums中的元素
return true;//下一个元素能放进桶中
}
bucket[j] -= nums[i];//回溯状态
}
return false;//循环结束都没放进合适的桶 那不能构成正方形
}
if (nums.length < 4) {//nums长度小于4 直接不能构成正方形
return false;
}
let sum = 0;
for (let i = 0; i < nums.length; i++) {
sum += nums[i];
}
if (sum % 4) {//nums的和不能整除4 不能构成正方行
return false;
}
nums.sort((a, b) => b - a);//排序nums
let bucket = Array(4).fill(0);//准备4个桶
return backtrack(0, nums, sum / 4, bucket);//传入nums元素的索引i,nums,一个边长,和桶bucket
};