Monte-Carlo Dropout（蒙特卡罗 dropout），Aleatoric Uncertainty，Epistemic Uncertainty

深度学习中的两个不确定性

偶然不确定性

偶然不确定性(Aleatoric Uncertainty，AU)又称为数据不确定性，是由于观测数据本身的噪声产生的（人脸不清楚，标注框边缘不准确······），偶然不确定性是无法通过获取更多的观测数据来降低的。

认知不确定性

认知不确定性(Epistemic Uncertainty，EU)又称为模型不确定性，是由于模型参数的不确定性、模型结构的不确定性产生的，即模型训练的不是很好，所以模型得出来的结果不是结果存在不确定性。

Monte-Carlo Dropout（蒙特卡罗 dropout）

Monte-Carlo Dropout( 蒙特卡罗 dropout )，简称 MC dropout , 想要深入了解理论推导可以看原论文：
Dropout as a Bayesian Approximation:Representing Model Uncertainty in Deep Learning
这里只做简单介绍：

对于一个模型的输出结果，我们想得到这个结果的方差来计算模型不确定性（认知不确定性）。而模型的参数是固定的，一个单独输出值是得不到方差的。如果说——我们能够用同一个模型，对同一个样本进行T次预测，而且这T次的预测值各不相同，就能够计算方差。

问题是同一个模型同一个样本，怎么得到不同的输出呢？我们可以让学到的模型参数不是确定的值，而是服从一个分布，那么模型参数就可以从这个分布中采样得到，每一次采样，得到的模型参数都是不同的，这样模型产生的结果也是不同的，我们的目的就达到了。

但是如何让模型的参数不是确定的而是服从一个分布呢？ 现成的dropout就是,使用dropout来训练模型时，模型的参数可以看成是服从一个伯努利分布（比如dropout radio =0.5，一种说法是：这层神经元中有一半会被dropout，换种说法就是——这层的每个神经元都有0.5的概率被dropout，这就是伯努利分布）。但是我们估计模型不确定度肯定是在训练好的模型上，也就是测试模型时估计的。所以我们只需要在预测的时候，仍然将dropout打开，预测 $T$ 次，取预测的平均值就是最终的预测值。并且通过平均值就可以得到方差，这样就得到深度学习的不确定度了。这种方法也被称为MC Dropout贝叶斯神经网络。

估计不确定性

我们估计不确定性的目的是：估计模型对输出结果的不确定性。
同时，因为我们模型在对样本计算的时候，偶然不确定性已经存在于样本数据中，已经影响到了我们模型的输出结果，所以实际上我们对模型的输出结果进行不确定性估计的时候就是同时将偶然不确定性和认知不确定性同时估计了。
估计的方法，我们可以采用MC dropout。

对于回归问题，不确定性可以用输出值的方差来表示： $\frac{1}{T}\sum _{t=1}^T(f^{{\hat{W}}_t}(x)-E(y){)}^2$

其中，$E(y)=\frac{1}{T}{\sum }_{t=1}^T{f}^{{\hat{W}}_t}(x)$表示输出的平均值。

对于分类问题， $T$ 次预测的概率为：
其中 ${\hat{W}}_t\backsim q_{\theta }^{\ast }(W)$ ，就是每次采样的模型参数。
不确定性可以用熵来衡量：$H(p)=-\sum _{c=1}^C{p}_c\log p_c$

利用不确定性训练模型

回归任务

为了将两种不确定性结合到同一个模型中，我们需要两组输出：一组是最终的预测结果 $\hat{y}$，另一组是样本的偶然不确定性 $\hat{\sigma }$ 。即:

通过最小化以下的损失函数来训练模型：

其中 $D$ 表示样本数量， $i$ 为像素的索引。上面的损失包含了两部分：一部分是回归模型的残差，用于捕获模型参数的认知不确定性；另一部分是像素点的偶然不确定性，充当正则化项。注意到，在学习偶然不确定性时，其实是不需要为方差 ${\hat{\sigma }}_i$ 额外标注标签的。
因为如果当一个样本 $i$ 很难预测对，为了最小化整个损失， ${\hat{\sigma }}_i$ 会相应地变大，而 $\frac{1}{2}\log {\widehat{{\sigma }_i}}^2$ 又会防止 ${\hat{\sigma }}_i$ 变得无穷大。
所以并不需要 $\hat{\sigma }$ 的真实标签。

注：损失函数公式的并不是随便给出的，而是可以由数学推导得到的，上面的文字只是对公式做了解释。

实际训练中， ${\hat{\sigma }}_i^{-2}$ 其实相当于一项自适应的权重，对于难以预测的样本，数据中存在较多的固有噪声，这项权重比较小；而对于容易预测的样本，数据中存在的固有噪声比较少，这项权重会比较大。这会让模型在训练过程中区别地对待不同的样本。

分类任务

在分类任务中，对于一个样本 $i$，模型会输出一个预测向量 \large f${}_i$ ，然后再通过softmax操作得到一组概率 $p_i$。假定预测向量服从高斯分布：
这里 \large f${}_i^W$ 和 $\sigma {}_i^W$ 是网络参数为 $W$ 时的输出(个人认为就是模型同时学习 \large f${}_i^W$ 和 $\sigma {}_i^W$ )。相当于对向量 f${}_i^W$ 施加了一个方差为 $\sigma {}_i^W$ 的噪声。

训练模型的损失函数可以写为:
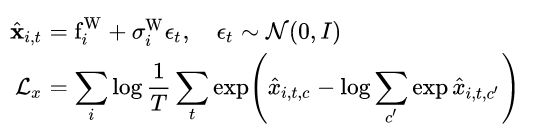其中，第二项，也就是损失函数项，实际上就是交叉熵损失函数进一步变形后的结果。
简单推导：
假定一共有C个类别，样本 $i$ 属于类别 $c$，$y_{i,c^{\prime }}\in$ {0,1}，那么样本的交叉熵损失为:

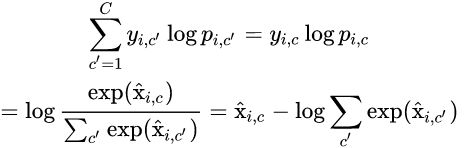
因为要执行T次预测，因此损失也要取T次的平均，最后取对数就得到了上面的损失函数公式。

至于方差$\sigma {}_i^W$的学习和${\hat{x}}_{i,t}$的采样，其实就是运用 reparemerization 的技巧，详情可以参考VAE的内容。
变分自编码器（Variational Auto-Encoder，VAE）

参考文章：
深度学习中的不确定性

论文：
What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? (NIPS 2017)