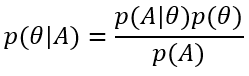双月数据生成及其常见算法(二)

算法部分：

数据使用：双月数据生成及其常见算法(一)_防空洞的仓鼠的博客-CSDN博客  文章中的数据

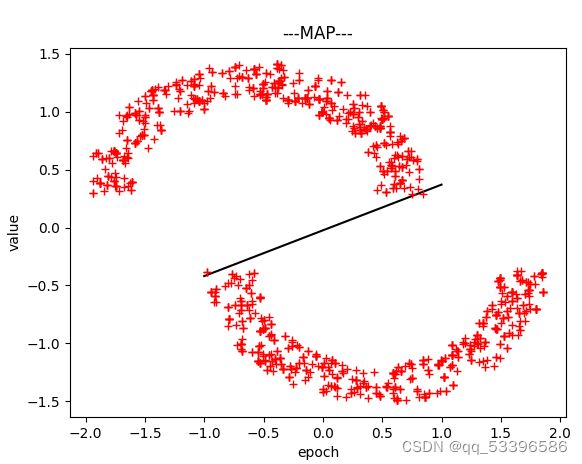
（一）最小二乘：

理论部分：

通过矩阵求解方式，来获取最优参数。具体求解B则为我们所需要的最佳解。X为对应的数据，Y是对应的输出。 

代码实现：

其中trainData是对应的数据数据，target则为对应标签。

#最小二乘算法
    def MIN2X(self, trainData,target):
        self.w = np.array((trainData.T*trainData).I*trainData.T*target[:,2:])
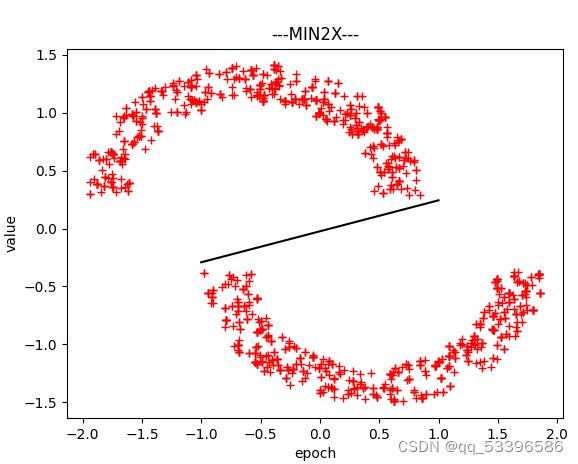
        print("MIN2X更新后的权重为:{}".format(self.w))

（二）ML：最大似然估计

理论部分：

最大似然估计是概率论中常常涉及到的一种统计方法。最大似然估计会寻找关于θ的最可能的值，即在所有可能的θ取值中，寻找一个值使这个采样的“可能性”最大化。

现在，我们的目标就是最大似然函数：。

 最大化对数似然函数，实际上就是最小化平方和误差函数，以此找到最大似然解。

根据公式推导：最优化解的形式为：

W(ML)  = Rxx.I(N)*Rdx(N)

其中Rxx为自相关矩阵，Rdx则为互相关矩阵。

Rxx(N) = x*x.T            Rdx(N) = x*d 

通过带入X以及对应的响应d，则能够得到该部分数据的ML最优参数解。

代码部分：

#ML算法
    def ML(self, TrainData, target):
        Rxx = TrainData.T * TrainData
        Rdx = TrainData.T * target[:, 2:]
        self.w = np.array(Rxx.I*Rdx)
        print("ML更新后的权重为:{}".format(self.w))

（三）MAP：最大后验估计

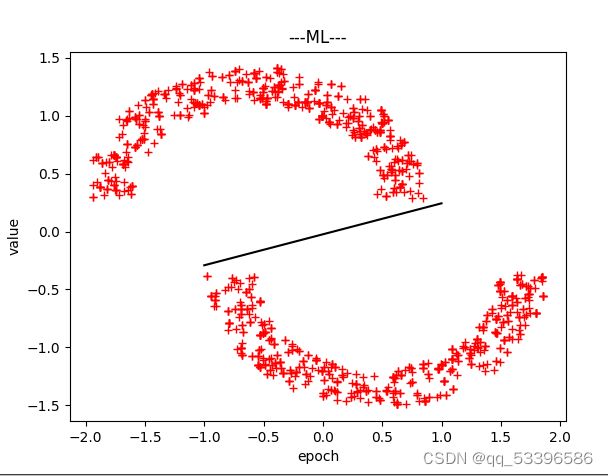
理论部分：最大似然估计不同的是，最大后验估计寻求的是能使后验概率最大的值。通常是：通过参数的先验分布结合样本信息得到参数的后验分布。

本质上不同于ML估计，MAP估计是有偏估计，ML是无偏估计。

代码部分：

  #MAP算法
    def MAP(self,TrainData,target):
        Rxx = TrainData.T*TrainData
        Rdx = TrainData.T*target[:,2:]
        self.w = np.array((Rxx+self.lamba*np.eye(len(TrainData.T))).I*Rdx)
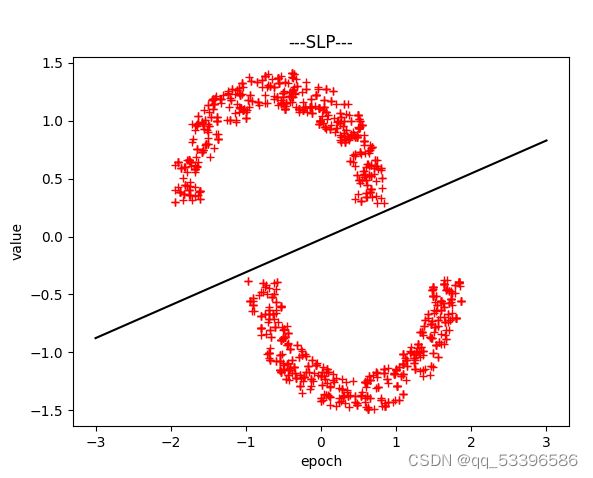
        print("MAP更新后的权重为:{}".format(self.w))

（四）SLP：单层感知机

理论部分：通过迭代思想，来对参数的优化，使得求解出一组误差较小的最优解。

代码部分：

      def SLP(self,trainData,target):
        ERROR = []
        allNumbel = len(trainData)
        for i in range(self.epoch):
            errorNumbel = 0
            for x, y in zip(trainData, target):

                if y[2] != sign(np.dot(self.w.T, x)):
                    errorNumbel = errorNumbel + 1
                    self.w = self.w + self.lr * sign(y[2] - np.dot(self.w.T, x))*x

            ERROR.append(errorNumbel/allNumbel)

        print("LMS更新后的权重为:{}".format(self.w))
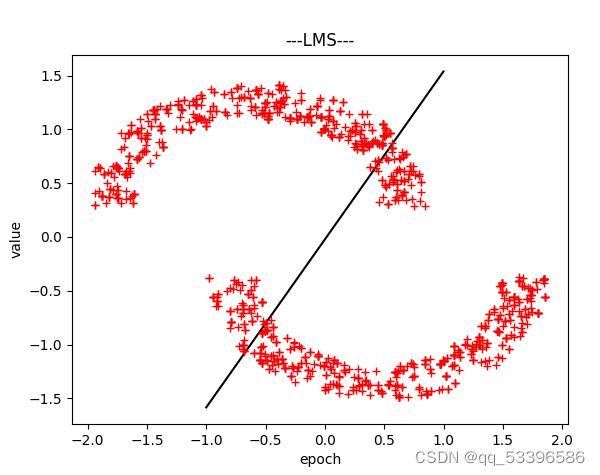
        return ERROR

（五）LMS：

理论部分：通过不断迭代，寻找一组权值向量，使得预测和期望之间的误差最小化。进而不断地优化参数。

E(w∗)≤E(∀w)

一般方法是不断迭代使 E(w(i))

代码部分：

 # 最小二乘算法
    def LMS(self, trainData, target):
        ERROR = []
        allNumbel = len(trainData)
        for i in range(self.epoch):
            errorNumbel = 0
            for x,y in zip(trainData,target):
                x = np.squeeze(x.tolist())
                y = np.squeeze(y.tolist())

                if y[2] != sign(np.dot(self.w.T, x)):
                    errorNumbel = errorNumbel + 1

                err = y[2] - x.T * self.w
                self.w = self.w + self.lr * x * err
            ERROR.append(errorNumbel/allNumbel)

        print("LMS更新后的权重为:{}".format(self.w))
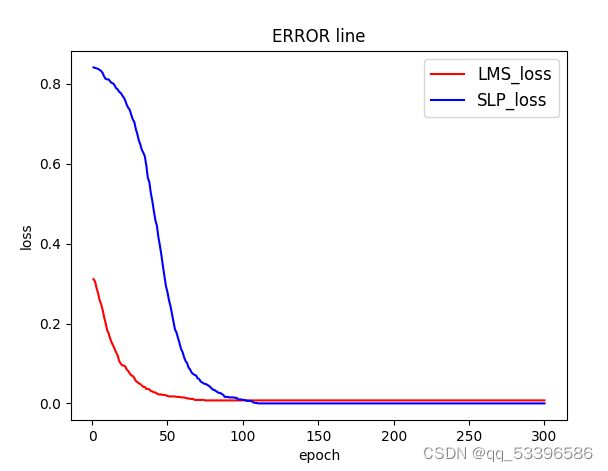
        return ERROR

结果：

 

 

 

 以上为仅讨论线型可分情况下的类型，分类和决策平面，以及完成代码放以下链接

双月数据及其分类算法.zip-机器学习文档类资源-CSDN下载