随机过程对定量融资的许多方面都很有用,包括但不限于衍生品定价,风险管理和投资管理。这些应用程序将在本文后面进一步详细讨论。本节介绍了量化融资中使用的一些流行的随机过程及其在Python中的实现。
模型参数
模型参数类包含以下随机过程使用的所有参数。为了便于理解,这些参数的前缀是它们所用的随机过程的名称。随机过程的校准将涉及寻找与某些历史数据相符的参数值。对于那些感兴趣的校准,将在我博客后面的后续帖子中讨论。
绘制结果图
下面的代码使用Matplotlib来绘制一组随机过程。
布朗运动随机过程
布朗运动 是由悬浮在气体或液体中的颗粒表现出的随机运动。这种随机运动是由颗粒与液体或气体中的原子或分子碰撞引起的。布朗运动以植物学家罗伯特·布朗的名字命名,他观察了1827年的随机运动。布朗运动与金融市场之间的关系可以追溯到1900年路易斯·巴舍利尔撰写的题为“投机理论 ” 的论文。 他的论文是第一个提出使用布朗运动来评估股票期权的论文。这篇论文直到后来才得出由Fisher Black和Myron Scholes于1973年开发的着名的Black Scholes期权定价公式。在金融中使用的随机过程的背景下,Brownian Motion经常被描述为Wiener过程,用表示t。Wiener过程由以下属性描述,WtWt
W0=0W0=0
函数是连续的t→Wtt→Wt
具有独立的正态分布增量,即Wt-Ws ~N(0,t-s)WtWtWt−WsWt−WsN(0,t−s)N(0,t−s)
在实践中,布朗运动不用于模拟资产价格。我已将其包含在内,因为它是本文中讨论的每个其他随机过程的基础。
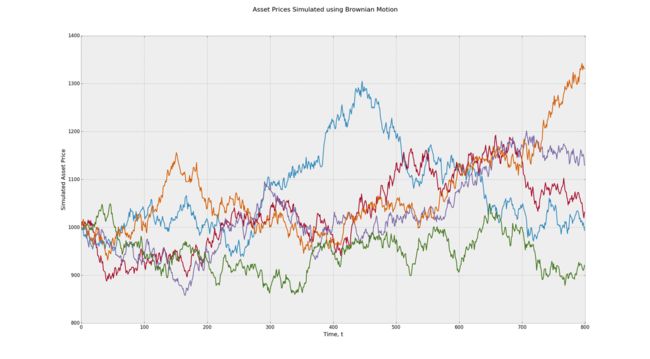
以下是此方法生成的输出示例。请注意,平均而言,生成的路径不会随着时间的推移而向上或向下漂移,换句话说,预期的回报为零。
使用布朗运动随机过程模拟资产价格
几何布朗运动随机过程
几何布朗运动(GBM)由费舍尔布莱克和迈伦斯科尔斯推广,他们在1973年的论文“期权定价和公司负债”中使用它来推导出Black Scholes方程。几何布朗运动基本上是布朗运动,具有漂移分量和波动率分量。描述几何布朗运动随机过程演化的随机微分方程是,
dSt=μStdt+σdStWtdSt=μStdt+σdStWt
其中是资产价格S在时间t的变化 ; μ是每年预期的百分比漂移,dt代表时间(1dStdStSSttμμdtdt用于每日变化),σ是资产价格中预期的每日波动率,Wt是Wiener过程,也称为布朗运动。如下所示,布朗运动代码用于几何布朗运动方法以构造Wt的序列。12521252σσWtWtWtWt
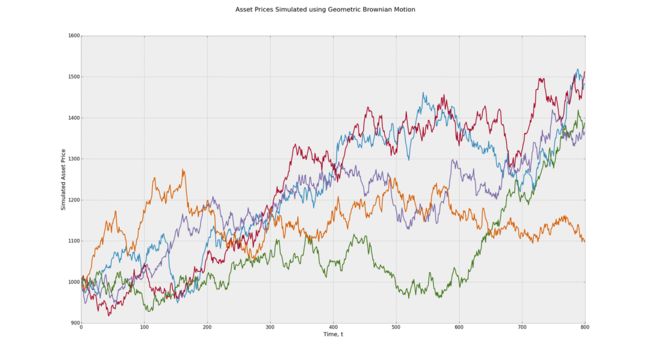
以下是此方法生成的输出示例。请注意,平均而言,生成的路径随着时间的推移而向上漂移,并且可能的结束价格变化较大。在这个例子中,路径以每年14%的平均速率增长,因此预期回报率等于14%,分别为三年和一年(800天)。
使用几何布朗运动随机过程模拟资产价格
默顿跳跃扩散随机过程
Robert C. Merton是最早解决Fisher Black和Myron Scholes提出的几何布朗随机过程中一些局限性的学者之一。1997年,默顿和斯科尔斯因其工作获得了诺贝尔经济学奖; 不幸的是,黑人在那个时候去世了。默顿提出的随机过程之一解决了连续几何布朗运动模型中不连续性的问题。
默顿扩展了原有的几何布朗运动过程跳扩散过程 在他1976年纸, 期权定价时,标的股票的收益是不连续的。有关基础跳扩散过程的数学的深入讨论,请参见,一个 简介扩散和跳扩散Processe小号 但在摘要中的随机过程增加了一个跳跃过程如化合物泊松过程到下面的扩散工艺,例如几何布朗运动。在下面的代码中,jump组件称为jump_sizes,
dSt=μStdt+σStdWt+dJtdSt=μStdt+σStdWt+dJtJtJt
dJt=Std(∑Nti=0(Yi−1))dJt=Std(∑i=0Nt(Yi−1))
其中是具有速率泊松过程λ和ÿ我是如下的对数正态分布的随机变量。NtNtλλYiYi
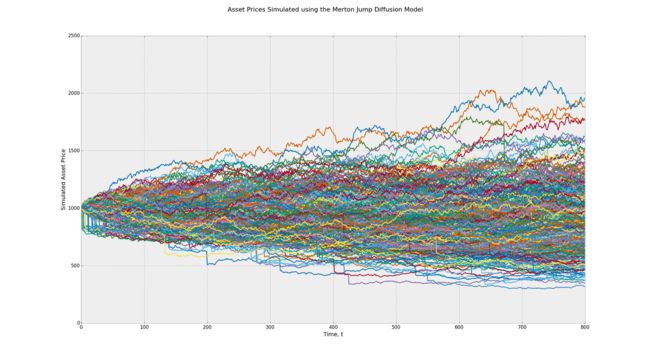
请注意,由于跳跃扩散过程引入了向下的不连续或跳跃,因此资产的平均预期收益率略低。这种不连续性可能代表市场崩溃。如果平均跳跃幅度为正,它们可能代表非常短时间内的市场高峰,这也可能发生。
使用默顿跳跃扩散几何布朗运动随机过程模拟资产价格
赫斯顿随机波动率过程
原始的几何布朗运动随机过程假设随时间的波动是恒定的。在1990年代早期,Steven Heston放宽了这个假设,并将几何布朗运动模型扩展到包括随机波动率。生成的模型称为 Heston模型。 根据Cox Ingersoll Ross随机过程,在Heston模型中随时间的波动性随时间演变。因此,该模型用于两个Wiener过程,一个用于Cox Ingersoll Ross过程,另一个用于几何布朗运动过程,该过程使用Cox Ingersoll Ross过程作为波动率。这两个Wiener过程是相关的,可以使用Cholesky分解来构造。
Heston模型的随机微分方程如下:
dSt=μStdt+vt−−√StdWStdSt=μStdt+vtStdWtS
(Cox Ingersoll Ross),和dvt=a(b−vt)dt+σvt−−√dWvtdvt=a(b−vt)dt+σvtdWtv
是资产的漂移,WS和Wv是两个相关的Wiener过程,其中相关性由下式给出μμWSWSWvWv,a是Cox Ingersoll Ross过程的均值回归率,b是随时间的平均值(在在这种情况下,平均波动率随时间变化),σ是Cox Ingersoll Ross过程的波动率。术语a(b-vt) 也称为漂移因子。
为了关联两个Wiener过程,我们将矩阵乘以不相关的Wiener过程与我们希望产生的相关矩阵的Cholesky分解。Cholesky分解技术将相关矩阵(正定矩阵)分解为其下三角矩阵(或上三角矩阵)与其共轭转置的乘积。
Heston模式的代码,创建两个相关Wiener过程的捷径方式,以及传统的n-asset Cholesky分解如下所示,
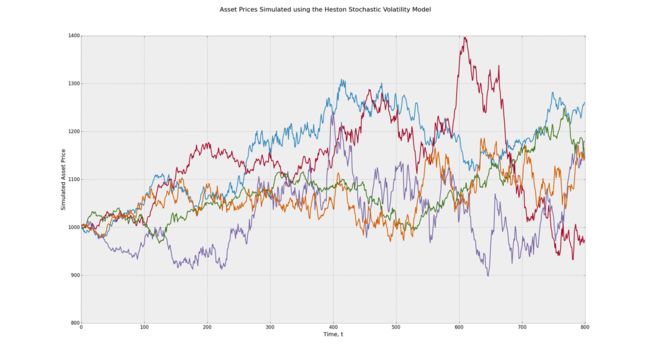
请注意,随着时间的推移,资产价格会变得更加不稳定,从而导致潜在资产价格在预测结束时飙升。出现这种现象是因为我将长期平均波动率设定为远高于起始波动率的数字。
使用Heston随机波动率几何布朗运动随机过程模拟资产价格
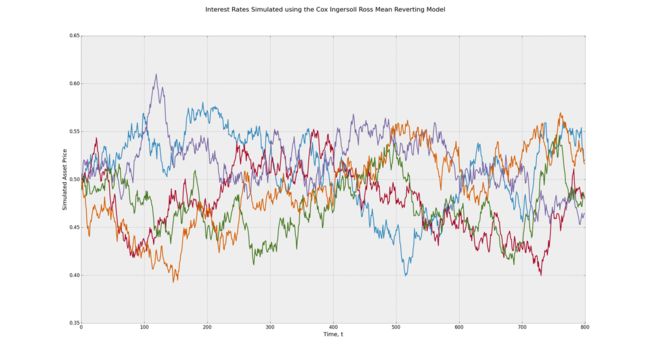
COX INGERSOLL ROSS随机过程
在考克斯英格索兰罗斯(CIR) 随机过程是用来描述一段时间的利率变化。CIR随机过程最初由John Cox,Johnathan Ingersoll和Stephen Ross于1985年引入。CIR过程是Ornstein Uhlenbeck随机过程的扩展。随机过程通常用于利率衍生工具的估值,并已在赫斯顿模型中用于描述波动率随时间的演变。CIR随机过程的一个有趣特征是它是均值回复。均值回归是一种水平趋向于随时间推移向平均水平移动的现象。换句话说,如果平均利率为0.5%,并且我们模拟500个独立的CIR流程,我们预计预测期结束时的平均利率约为0.5%。CIR过程的随机微分方程由下式给出,
drt=a(b−rt)dt+σrt−−√dWtdrt=a(b−rt)dt+σrtdWt
其中是Wiener过程,a是过程均值恢复的速率(较大的数字导致更快的均值回复过程),b是长期平均利率,σ是过程的波动率。CIR随机过程的代码如下。WtWtaabbσσ
请注意,当利率偏离长期平均利率时,它倾向于“改变方向”并再次接近均值。这称为均值回归,由术语。
利用Cox Ingersoll Ross均值回归随机过程模拟利率
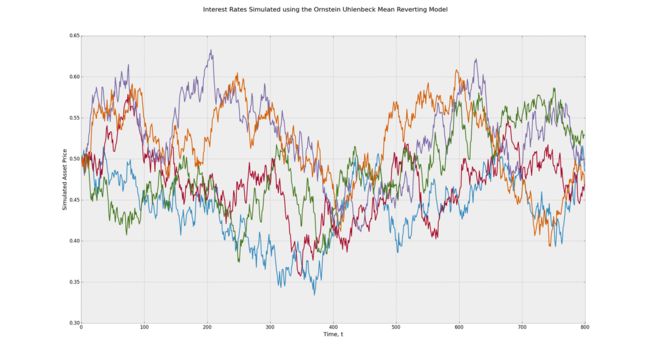
ORNSTEIN-UHLENBECK随机过程
该奥恩斯坦Uhlebneck随机过程是另一种均值回归的过程,有时用于建模的利率。Ornstein Uhlenbeck过程以Leonard Ornstein和George Eugene Uhlenbeck命名。Ornstein Uhlenbeck随机过程与CIR过程之间的区别在于CIR过程将随机分量乘以前一个利率值的平方根。Ornstein Uhlenbeck过程的随机微分方程是,
其中是Wiener过程,a是过程均值恢复的速率(较大的数字导致更快的均值回复过程),b是长期平均利率,σ是过程的波动率。
利用Ornstein Uhlenbeck均值回归随机过程模拟利率
衍生品定价和套期保值的随机过程
随机过程在量化金融中的最大应用是衍生品定价。本节将介绍衍生物背后的基本概念,并描述如何使用随机过程使用封闭形式解决方案(如Black Scholes公式或使用蒙特卡罗方法)对其进行数值定价。
甲衍生物是从一些标的证券的性能得到其值的合同。共同基础包括市场指数,金融资产,利率和波动性。一般而言,衍生品通过柜台衍生品(OTC)或通过交易所或其他中介进行买卖。交易所交易衍生品的价格等于它们在市场上交易的价格。由于场外交易衍生品直接在双方之间买卖,衍生品的公允价格必须使用定量技术计算。
当对柜台衍生品进行定价时,大多数量子将使用两种方法中的一种。他们要么为他们定价的衍生物解决(或找到解决方案)Black Scholes模型,要么他们将使用模拟方法来估计导数的值。这两种技术都严重依赖于使用随机过程来模拟底层证券。
衍生定价方法一 - 黑斯科尔斯
Black Scholes模型用于在一组假设下对特定类型的衍生品合约进行定价。这些假设包括:(1)存在无风险利率,任何金额可以借入或借出,(2)基础价格根据几何布朗运动随机过程(稍后讨论),(3)进化基础不支付股息,(4)市场上没有套利机会,(5)市场无摩擦意味着交易成本为零,(6)可以买入或减去任何数量的潜在的。
在这些假设下,可以导出着名的Black Scholes偏微分方程。
该公式断言,期权价格相对于基础S是两次可微分,并且相对于时间t是一次。因此,如果期权的收益是,由于缺乏更好的词,很奇怪,可能无法使用Black Scholes偏微分方程。在这种情况下,您可能不得不求助于使用方法二。Black Scholes偏微分方程告诉我们,衍生物的价格将如何随着时间的推移而与潜在的随机过程相关。它尚未告诉我们衍生品的价格。为了得出衍生定价公式,您还需要求解给定导数的偏微分方程,例如欧洲看涨期权和看跌期权。VV小号SŤt
Black Scholes公式以及各种封闭形式期权定价公式的推导,是过去三十年中衍生品交易所大量增长的主要原因。
值得一提的是,“偏导数”可能不是Black Scholes公式解释中最好的数学解释,因为是一个随机过程,因此根据定义是不可微分的。小号S
导数定价 方法二 - 模拟方法
鉴于Black Scholes公式隐含的局限性和假设,通常采用蒙特卡罗方法(模拟)来为更少的简化假设定价更多的奇异衍生品甚至香草衍生物。例如,您可能希望放宽简化的假设,即基础跟随几何布朗运动,支持替代随机过程。在此示例中,您有两个可用选项,
您可以推导出替代随机过程的一般偏微分方程,然后仍然求解该导数的偏微分方程,或者
这两个选项在计算复杂性和时间之间进行权衡。每次想要对导数进行定价时,使用模拟方法计算复杂度更高,但是为替代随机过程推导Black Scholes偏微分方程的“等价”更加耗时,然后仍然找到封闭形式的衍生品定价式。因此,大多数量子使用模拟方法。
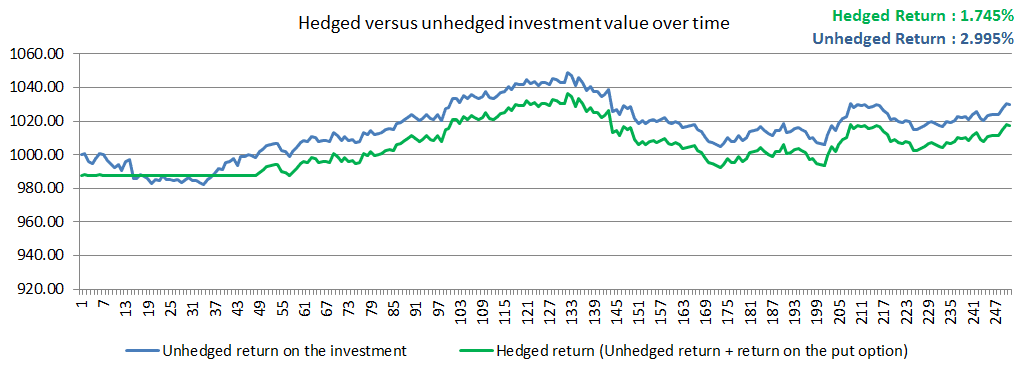
您想要这样做的原因如下图所示。事实上,你如何选择和校准你的随机过程将对期权的预期收益产生重大影响,因此它的价值也是如此。
红色椭圆形显示市场跳跃的位置(迷你崩溃)
使用衍生工具进行套期保值
套期保值是风险管理战略,旨在减少的量可对冲风险的投资组合暴露。可对冲风险包括股票风险,利率风险,货币风险,信用风险,波动风险和商品风险。套期保值是通过投资与投资组合中的基础负相关的资产来完成的。最简单的例子是在股票上买入看跌期权。当股票表现不佳时,看跌期权表现良好,而整体投资组合并没有像没有对冲时那样糟糕。净效应是抑制回报或下降。
对套期中的每个头寸进行套期保值并不总是可行的。因此,公司和基金将尝试确定投资组合所面临的风险因素并对冲这些风险因素。这是通过使用定量风险模型来完成的,该模型考察了投资组合对市场变化的敏感性。如果很好地理解这些敏感性,可能会购买衍生品以降低投资组合的敏感度。例如,鉴于对波动性,利率变化和货币波动敏感的宏观均衡投资组合,投资组合经理可能能够使用掉期交易(如波动率掉期,利率掉期和货币掉期)来降低投资组合风险。
话虽如此,人们必须记住两件事。首先,风险和收益是反相关的,这意味着经理对冲的风险越大,收益应该越小。事实上,如果投资组合面临的所有风险因素,他或她应该期望投资组合返回“无风险利率”。因此,投资组合经理可能会选择仅对冲其投资组合的一部分或对冲特定的风险因素。其次,这假设定量模型能够准确地衡量投资组合所面临的风险。模型不正确或不完整的风险称为模型风险。模型风险可能来自不确定性,时间不确定性,相关性不确定性,市场非流动性,债务抵押债券)。
正如你所看到的,套期保值肯定不是银弹。除了我上面提到的问题之外,还有一些额外的“现实世界”问题。一个例子是一般成本和套期保值程序的复杂性(套期保值可能非常昂贵)。对于组织而言,问题在于,在出现不利损失的情况下,对冲风险或仅仅保留更多资本是否更便宜。近年来,诸如Solvency II和Basel III等法规要求银行,对冲基金和保险公司预留更多资金来支持其投资组合。储备通常保留在高流动性证券中,预期收益很低,如国库券。
结论
随机过程对于描述我们周围世界中发现的随机过程非常有用。它们用于工程,遗传学,物理学和定量金融。数量使用随机过程来预测市场可能的回报和利率随时间的变化。随机过程通常与蒙特卡罗方法结合使用,以得出非处方衍生工具的公允价值。存在许多随机过程,这些过程在不同的假设下运行。可以说随机过程的最大挑战是它们的校准。校准是一个优化问题,随机过程的“最佳”参数值来自历史回报。将来我会写一篇关于量子可用的不同校准技术的后续文章
还有问题吗?联系我们!
大数据部落 -中国专业的第三方数据服务提供商,提供定制化的一站式数据挖掘和统计分析咨询服务
统计分析和数据挖掘咨询服务:y0.cn/teradat(咨询服务请联系官网客服)
【服务场景】
科研项目; 公司项目外包;线上线下一对一培训;数据采集;学术研究;报告撰写;市场调查。
【大数据部落】提供定制化的一站式数据挖掘和统计分析咨询服务