Python，OpenCV中的K均值聚类——K-Means Cluster

这篇博客将介绍什么是 K-Means 聚类以及 如何使用 cv2.kmeans() 函数进行数据聚类。

• K-Means Cluster K均值聚类
• cv2.kmeans() 进行数据聚类

1. 效果图

抽样生成5堆点后聚类，分别以不同的颜色绘制每一种分类，效果图1如下：

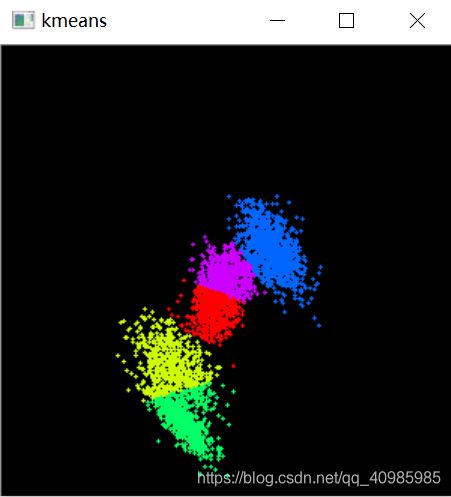
同样生成5堆点聚类5，得到效果图如下：

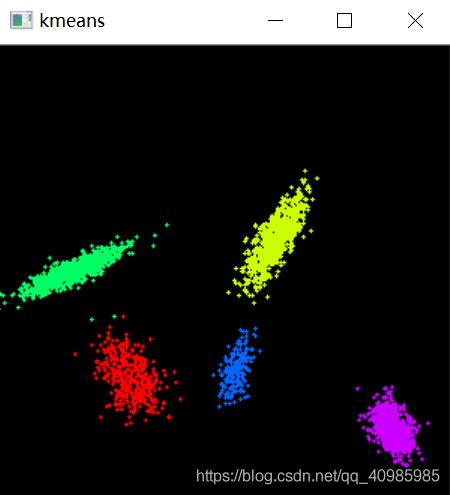
抽样生成10堆点后聚类，效果图如下:

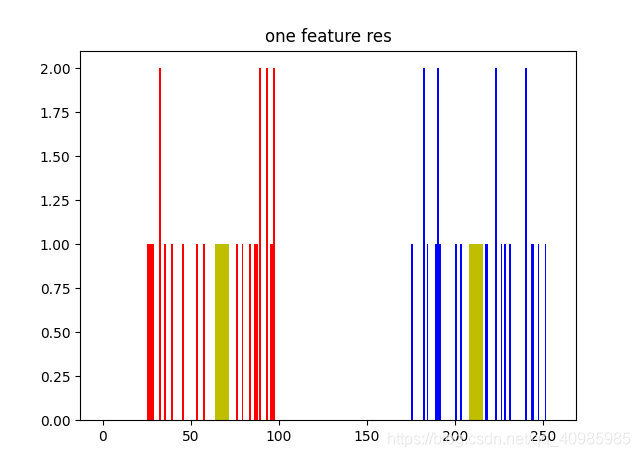
单特征聚类图：
T恤size只根据身高进行分类为3种

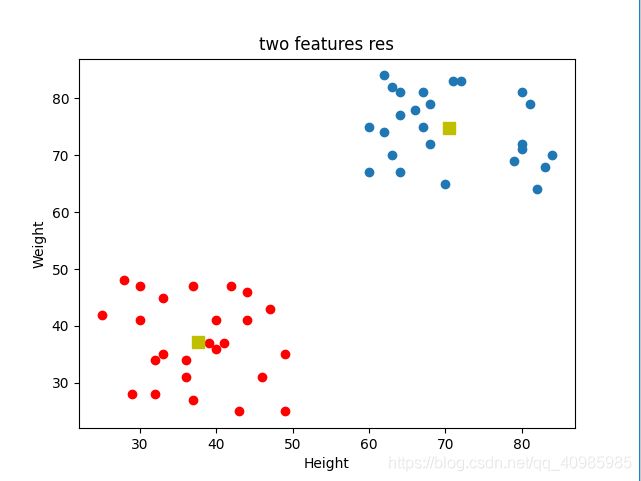
2个特征聚类图：
T恤size根据身高和体重共同来进行聚类，

颜色量化以减少色彩数量，并且得到新的图像，原图 VS 聚类15种色彩效果图如下：

聚类色彩数越多，算法要相对慢一些，但看起来跟原图越接近。

2. 原理

2.1 什么是K均值聚类？

考虑一家公司将向市场推出一种新型 T 恤。显然，他们将不得不制造不同尺寸的模型以满足各种尺寸的人。于是公司做了一个人的身高体重数据，绘制成图表，如下图：

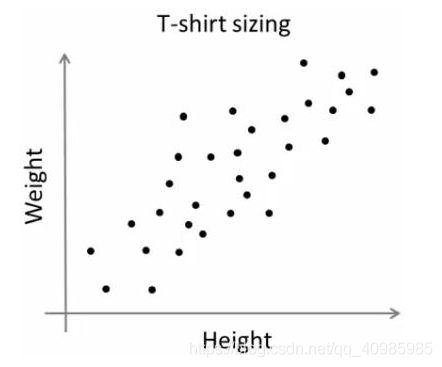
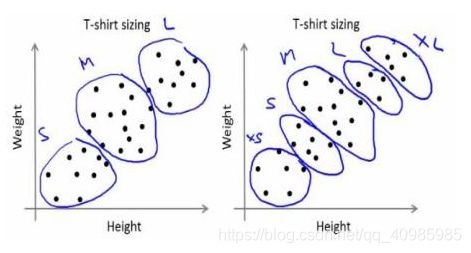
公司无法生产所有尺寸的 T 恤。相反，他们将人分为小、中、大，只生产这三种适合所有人的型号。这种将人分成三组可以通过 k-means 聚类来完成，算法为我们提供了最好的 3 种尺寸，这将满足所有人的需求。如果没有，公司可以将人分成更多组，可能是五个，如下图：

2.2 K均值聚类过程

K均值聚类是一个迭代过程，最基本的K均值聚类有以下4个步骤。

1. 假设有一堆点，要分成2类；

2. 随机选择俩个点C1，C2作为质心，计算周围点到C1，C2的距离，距离C1近则归入C1类，距离C2近则归入C2类。

3. 分割完后，计算C1类所有点的平均值作为C1的新质心，计算C2类所有点的平均值作为C2的新质心；

4. 迭代2，3过程，根据设置的条件终止（迭代过程达到多少次，或达到设置的精度）终止。

5. 最终的收敛是C1到其所有点的距离 + C2到其所有点的距离 = 最小值。
   

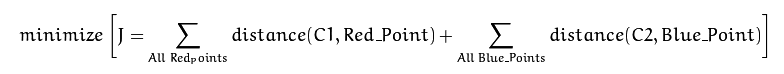
   这些点使得测试数据与其对应的质心之间的距离之和最小。

以上4步只是 K-Means 聚类的顶层。该算法有很多优化，例如：如何选择初始质心，如何加快迭代过程。

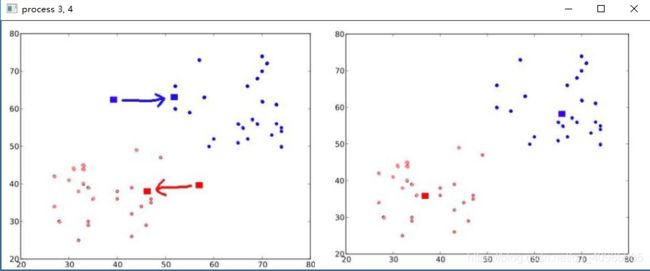
该迭代过程可以用以下图片近似表示，分别代表以上4个过程。

下图迭代1，2步骤，随机选中点作为质心点，计算距离进行分类；

下图重新计算质心后迭代3，4步骤然后得到结果图，可以看到多次迭代后随机点被分成2堆点，红色，蓝色；质心点也相对居中，比较规整。

2.3 cv2.kmeans(z, 2, None, criteria, 10, flags)

compactness, labels, centers = cv2.kmeans(z, 2, None, criteria, 10, flags)

入参:

• samples: np.float32 数据类型，每个特征放在一个列中。
• nclusters(K) : 最后需要的簇数
• creteria: 迭代终止标准。当满足此条件时，算法迭代停止。实际上，它应该是一个包含 3 个参数的元组。
  （type、max_iter、epsilon）:
  a - 终止条件的类型：它有 3 个标志，cv2.TERM_CRITERIA_EPS - 如果达到指定的准确度 epsilon，则停止算法迭代。cv2.TERM_CRITERIA_MAX_ITER - 在指定的迭代次数 max_iter 后停止算法。cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER - 当满足上述任何条件时停止迭代。
  b - 最大迭代次数 - 指定最大迭代次数的整数。
  c - 精度 - 要求的准确性
• attempts ：标记以指定使用不同的初始标签执行算法的次数。该算法返回产生最佳紧凑性的标签。这种紧凑性作为输出返回。
• flags ：此标志用于指定如何采用初始中心。通常为此使用两个标志：cv2.KMEANS_PP_CENTERS 和 cv2.KMEANS_RANDOM_CENTERS。

返回值：

• compactness: 紧凑度，指每个点到其相应中心的距离平方和
• labels: 标签数组，其中每个元素都标记为“0”、“1”…
• centers: 聚簇中心的数组

3. 源码

3.1 抽样生成点后聚类

# K均值聚类随机生成一堆点并聚类demo

from __future__ import print_function

import cv2 as cv
import numpy as np
from numpy import random


def make_gaussians(cluster_n, img_size):
    points = []
    ref_distrs = []
    for _i in range(cluster_n):
        mean = (0.1 + 0.8 * random.rand(2)) * img_size
        a = (random.rand(2, 2) - 0.5) * img_size * 0.1
        cov = np.dot(a.T, a) + img_size * 0.05 * np.eye(2)
        n = 100 + random.randint(900)
        pts = random.multivariate_normal(mean, cov, n)
        points.append(pts)
        ref_distrs.append((mean, cov))
    points = np.float32(np.vstack(points))
    return points, ref_distrs


def main():
    cluster_n = 5
    img_size = 300

    # 生成明亮的调色板
    colors = np.zeros((1, cluster_n, 3), np.uint8)
    colors[0, :] = 255
    colors[0, :, 0] = np.arange(0, 180, 180.0 / cluster_n)
    colors = cv.cvtColor(colors, cv.COLOR_HSV2BGR)[0]

    while True:
        print('sampling distributions...')
        points, _ = make_gaussians(cluster_n, img_size)

        term_crit = (cv.TERM_CRITERIA_EPS, 30, 0.1)
        _ret, labels, _centers = cv.kmeans(points, cluster_n, None, term_crit, 10, 0)

        img = np.zeros((img_size, img_size, 3), np.uint8)
        for (x, y), label in zip(np.int32(points), labels.ravel()):
            c = list(map(int, colors[label]))

            cv.circle(img, (x, y), 1, c, -1)

        cv.imshow('kmeans', img)
        ch = cv.waitKey(0)
        if ch == 27:
            break

    print('Done')


if __name__ == '__main__':
    print(__doc__)
    main()
    cv.destroyAllWindows()

3.2 单特征聚类、多特征聚类、颜色量化

# OpenCV实现K-Means Cluster K均值聚类
# 输入参数
# - samples: np.float32 数据类型，每个特征放在一个列中。
# - nclusters(K) : 最后需要的簇数
# - creteria: 迭代终止标准。当满足此条件时，算法迭代停止。实际上，它应该是一个包含 3 个参数的元组。它们是（类型、max_iter、epsilon）：
#  a - 终止条件的类型：它有 3 个标志，如下所示：cv2.TERM_CRITERIA_EPS - 如果达到指定的准确度 epsilon，则停止算法迭代。
#                                             cv2.TERM_CRITERIA_MAX_ITER - 在指定的迭代次数 max_iter 后停止算法。
#                                             cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER - 当满足上述任何条件时停止迭代。
# b - 最大迭代次数 - 指定最大迭代次数的整数。
# c - 精度 - 要求的准确性
# - attempts ：标记以指定使用不同的初始标签执行算法的次数。该算法返回产生最佳紧凑性的标签。这种紧凑性作为输出返回。
# - flags ：此标志用于指定如何采用初始中心。通常为此使用两个标志：cv2.KMEANS_PP_CENTERS 和 cv2.KMEANS_RANDOM_CENTERS。

#
# 输出参数
#
# - compactness: 紧凑度，指每个点到其相应中心的距离平方和
# - labels: 标签数组，其中每个元素都标记为“0”、“1”.....
# - centers: 聚簇中心的数组

# 1. 只有一个特征的数据（T恤问题，只根据身高）
import numpy as np
import cv2
from matplotlib import pyplot as plt

x = np.random.randint(25, 100, 25)
y = np.random.randint(175, 255, 25)
z = np.hstack((x, y))
z = z.reshape((50, 1))
z = np.float32(z)
plt.hist(z, 256, [0, 256]), plt.show()

# 每当运行 10 次算法迭代或达到 epsilon = 1.0 的准确度时，停止算法并返回
# 定义终止准则 criteria = ( type, max_iter = 10 , epsilon = 1.0 )
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# 设置标志（只是为了避免代码中的换行符）
flags = cv2.KMEANS_RANDOM_CENTERS

# 应用K均值聚类算法
compactness, labels, centers = cv2.kmeans(z, 2, None, criteria, 10, flags)

A = z[labels == 0]
B = z[labels == 1]

# 以红色绘制 A，以蓝色绘制 B，以黄色绘制它们的质心。
plt.hist(A, 256, [0, 256], color='r')
plt.hist(B, 256, [0, 256], color='b')
plt.hist(centers, 32, [0, 256], color='y')
plt.title("one feature res")
plt.show()

# 2. 具有多重数据的特征（T恤问题，根据身高、体重）
import numpy as np
import cv2
from matplotlib import pyplot as plt

X = np.random.randint(25, 50, (25, 2))  # 身高
Y = np.random.randint(60, 85, (25, 2))  # 体重
Z = np.vstack((X, Y))

# 转换为 np.float32
Z = np.float32(Z)

# 定义终止准则以及应用KMeans聚类
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
ret, label, center = cv2.kmeans(Z, 2, None, criteria, 10, cv2.KMEANS_RANDOM_CENTERS)

# 分离数据，并拉平flatten
A = Z[label.ravel() == 0]
B = Z[label.ravel() == 1]

# 绘制数据
plt.scatter(A[:, 0], A[:, 1])
plt.scatter(B[:, 0], B[:, 1], c='r')
plt.scatter(center[:, 0], center[:, 1], s=80, c='y', marker='s')
plt.xlabel('Height'), plt.ylabel('Weight')
plt.title("two features res")
plt.show()

## 3. 颜色量化
# 颜色量化是减少图像中颜色数量的过程。这样做的原因之一是减少内存。有时某些设备可能有限制，以至于它只能产生有限数量的颜色。
# 在这些情况下，也会执行颜色量化。这里我们使用 k-means 聚类进行颜色量化。有3个特征，例如 R、G、B。需要将图像重塑为 Mx3 大小的数组（M 是图像中的像素数）。
# 在聚类之后将质心值（也是 R、G、B）应用于所有像素，这样生成的图像将具有指定数量的颜色，最后需要将其重塑回原始图像的形状。
import numpy as np
import cv2

img = cv2.imread('images/ml.jpg')
Z = img.reshape((-1, 3))

# 转换 np.float32
Z = np.float32(Z)

# 定义终止准则以及应用KMeans聚类
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
K = 15
ret, label, center = cv2.kmeans(Z, K, None, criteria, 10, cv2.KMEANS_RANDOM_CENTERS)

# 转换回uint8, 制作原始图像
center = np.uint8(center)
res = center[label.flatten()]
res2 = res.reshape((img.shape))

cv2.imshow("origin",img)
cv2.imshow('res2', res2)
cv2.waitKey(0)
cv2.destroyAllWindows()

参考

• https://docs.opencv.org/3.0-beta/doc/py_tutorials/py_ml/py_kmeans/py_kmeans_understanding/py_kmeans_understanding.html#kmeans-clustering-understanding