深度强化学习(DRL)基础
深度强化学习(Deep Reinforcement Learning)是值得深入学习研究且非常有意思的领域,但是其数学原理复杂,远胜于深度学习,且脉络复杂,概念繁杂。强化学习是一个序贯决策过程,它通过智能体(Agent)与环境进行交互收集信息,并试图找到一系列决策规则(即策略)使得系统获得最大的累积奖励,即获得最大价值。环境(Environment)是与智能体交互的对象,可以抽象地理解为交互过程中的规则或机理,在围棋游戏中,游戏规则就是环境。强化学习的数学基础和建模工具是马尔可夫决策过程(Markov Decision Process,MDP)。一个MDP通常由状态空间、动作空间、状态转移函数、奖励函数等组成。
本文介绍与机巧围棋相关的深度强化学习基础知识,辅助理解描述阿尔法狗算法原理的强化学习语言。
1. 基本概念
-
状态(state):是对当前时刻环境的概括,可以将状态理解成做决策的唯一依据。在围棋游戏中,棋盘上所有棋子的分布情况就是状态。
-
状态空间(state space):是指所有可能存在状态的集合,一般记作花体字母 S \mathcal{S} S。状态空间可以是离散的,也可以是连续的。可以是有限集合,也可以是无限可数集合。在围棋游戏中,状态空间是离散有限集合,可以枚举出所有可能存在的状态(也就是棋盘上可能出现的格局)。
-
动作(action):是智能体基于当前的状态做出的决策。在围棋游戏中,棋盘上有361个位置,而且可以选择PASS(放弃一次落子权利),于是有362种动作。动作的选取可以是确定的,也可以依照某个概率分布随机选取一个动作。
-
动作空间(action space):是指所有可能动作的集合,一般记作花体字母 A \mathcal{A} A。在围棋例子中,动作空间是 A = { 0 , 1 , 2 , ⋯ , 361 } \mathcal{A}=\{0,1,2,\cdots,361\} A={ 0,1,2,⋯,361},其中第 i i i种动作是指把棋子放到第 i i i个位置上(从0开始),第 361 361 361种动作是指PASS。
-
奖励(reward):是指智能体执行一个动作之后,环境返回给智能体的一个数值。奖励往往由我们自己来定义,奖励定义得好坏非常影响强化学习的结果。一般来说,奖励是状态和动作的函数。
-
状态转移(state transition):是指从当前 t t t时刻的状态 s s s转移到下一个时刻状态 s ′ s^\prime s′的过程。在围棋的例子中,基于当前状态(棋盘上的格局),黑方或白方落下一子,那么环境(即游戏规则)就会生成新的状态(棋盘上新的格局)。
状态转移可以是确定的,也可以是随机的。在强化学习中,一般假设状态转移是随机的,随机性来自于环境。比如贪吃蛇游戏中,贪吃蛇吃掉苹果,新苹果出现的位置是随机的。
-
策略(policy):的意思是根据观测到的状态,如何做出决策,即从动作空间中选取一个动作的方法。策略可以是确定性的,也可以是随机性的。强化学习中无模型方法(model -free)可以大致分为策略学习和价值学习,策略学习的目标就是得到一个策略函数,在每个时刻根据观测到的状态,用策略函数做出决策。
将状态记作 S S S或 s s s,动作记作 A A A或 a a a,随机策略函数 π : S × A ↦ [ 0 , 1 ] \pi:\mathcal{S}\times\mathcal{A}\mapsto[0,1] π:S×A↦[0,1]是一个概率密度函数,记作 π ( a ∣ s ) = P ( A = a ∣ S = s ) \pi(a|s)=\mathbb{P}(A=a|S=s) π(a∣s)=P(A=a∣S=s)。策略函数的输入是状态 s s s和动作 a a a,输出是一个0到1之间的概率值。将当前状态和动作空间中所有动作输入策略函数,得到每个动作的概率值,根据动作的概率值抽样,即可选取一个动作。
确定策略是随机策略 μ : S ↦ A \mu:\mathcal{S}\mapsto\mathcal{A} μ:S↦A的一个特例,它根据输入状态 s s s,直接输出动作 a = μ ( s ) a=\mu(s) a=μ(s),而不是输出概率值。对于给定的状态 s s s,做出的决策 a a a是确定的,没有随机性。
-
状态转移函数(state transition function):是指环境用于生成新的状态 s ′ s^\prime s′时用到的函数。由于状态转移一般是随机的,因此在强化学习中用状态转移概率函数(state transition probability function) 来描述状态转移。状态转移概率函数是一个条件概率密度函数,记作 p ( s ′ ∣ s , a ) = P ( S ′ = s ′ ∣ S = s , A = a ) p(s^\prime |s,a)=\mathbb{P}(S^\prime=s^\prime |S=s,A=a) p(s′∣s,a)=P(S′=s′∣S=s,A=a),表示观测到当前状态为 s s s,智能体执的行动作为 a a a,环境状态变成 s ′ s^\prime s′的概率。
确定状态转移是随机状态转移的一个特例,即概率全部集中在一个状态 s ′ s^\prime s′上。
-
智能体与环境交互(agent environment interaction):是指智能体观测到环境的状态 s s s,做出动作 a a a,动作会改变环境的状态,环境反馈给智能体奖励 r r r以及新的状态 s ′ s^\prime s′。
-
回合(episodes):“回合”的概念来自游戏,是指智能体从游戏开始到通关或者游戏结束的过程。
-
轨迹(trajectory):是指一回合游戏中,智能体观测到的所有的状态、动作、奖励: s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , s 3 , a 3 , r 3 , ⋯ s_1,a_1,r_1,s_2,a_2,r_2,s_3,a_3,r_3,\cdots s1,a1,r1,s2,a2,r2,s3,a3,r3,⋯。
-
马尔可夫性质(Markov property):是指下一时刻状态 S t + 1 S_{t+1} St+1仅依赖于当前状态 S t S_t St和动作 A t A_t At,而不依赖于过去的状态和动作。如果状态转移具有马尔可夫性质,则 P ( S t + 1 ∣ S t , A t ) = P ( S t + 1 ∣ S 1 , A 1 , S 2 , A 2 , ⋯ , S t , A t ) \mathbb{P}(S_{t+1}|S_t,A_t)=\mathbb{P}(S_{t+1}|S_1,A_1,S_2,A_2,\cdots,S_t,A_t) P(St+1∣St,At)=P(St+1∣S1,A1,S2,A2,⋯,St,At)。
2. 回报与折扣回报
2.1 回报(return)
回报是从当前时刻开始到本回合结束的所有奖励的总和,所以回报也叫做累计奖励(cumulative future reward)。由于奖励是状态和动作的函数,因此回报具有随机性。将 t t t时刻的回报记作随机变量 U t U_t Ut,假设本回合在时刻 n n n结束,则 U t = R t + R t + 1 + R t + 2 + R t + 3 + ⋯ + R n U_t=R_t+R_{t+1}+R_{t+2}+R_{t+3}+\cdots+R_n Ut=Rt+Rt+1+Rt+2+Rt+3+⋯+Rn。
回报是未来获得的奖励总和,强化学习的一种方法就是寻找一个策略,使得回报的期望最大化。这个策略称为最优策略(optimum policy)。这种以最大化回报的期望为目标,去寻找最优策略的强化学习方法就是策略学习。
2.2 折扣回报(discount return)
假如我给你两个选项:第一,现在我立刻给你100元钱;第二,等一年后我给你100元钱。你选哪一个?相信理性人都会选择现在拿到100元钱,因为未来具有不确定性,未来的收益是会具有折扣的。即在强化学习中,奖励 r t r_t rt和 r t + 1 r_{t+1} rt+1的重要性并不等同。
在MDP中,通常会给未来的奖励做折扣,基于折扣奖励的回报即为折扣回报,折扣回报的定义为 U t = R t + γ R t + 1 + γ 2 R t + 2 + γ 3 R t + 3 + ⋯ U_t=R_t+\gamma R_{t+1}+\gamma^2R_{t+2}+\gamma^3R_{t+3}+\cdots Ut=Rt+γRt+1+γ2Rt+2+γ3Rt+3+⋯。其中 γ ∈ [ 0 , 1 ] \gamma\in[0,1] γ∈[0,1]为折扣率,对待越久远的未来,给奖励打的折扣越大。
由于回报是折扣率等于1的特殊折扣回报,下文中将“回报”和“折扣回报”统称为“回报”,不再对二者进行区分。
3. 价值函数(value function)
3.1 动作价值函数(action-value function)
回报 U t U_t Ut是 t t t时刻及未来所有时刻奖励的加权和。在 t t t时刻,如果知道 U t U_t Ut的值,我们就可以知道局势的好坏。 U t U_t Ut是一个随机变量,假设在 t t t时刻我们已经观测到状态为 s t s_t st,基于状态 s t s_t st,已经做完决策并选择了动作 a t a_t at,则随机变量 U t U_t Ut的随机性来自于 t + 1 t+1 t+1时刻起的所有的状态和动作: S t + 1 , A t + 1 , S t + 2 , A t + 2 , ⋯ , S n , A n S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_n,A_n St+1,At+1,St+2,At+2,⋯,Sn,An。
在 t t t时刻,我们并不知道 U t U_t Ut的值,但是我们又想估计 U t U_t Ut的值,解决方案就是对 U t U_t Ut求期望,消除掉其中的随机性。
对 U t U_t Ut关于变量 S t + 1 , A t + 1 , S t + 2 , A t + 2 , ⋯ , S n , A n S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_n,A_n St+1,At+1,St+2,At+2,⋯,Sn,An求条件期望,得到:
Q π ( s t , a t ) = E S t + 1 , A t + 1 , ⋯ , S n , A n [ U t ∣ S t = s t , A t = a t ] ( 1 ) Q_\pi(s_t,a_t)=\mathbb{E}_{S_{t+1},A_{t+1},\cdots,S_n,A_n}[U_t|S_t=s_t,A_t=a_t]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(1) Qπ(st,at)=ESt+1,At+1,⋯,Sn,An[Ut∣St=st,At=at] (1)
期望中的 S t = s t S_t=s_t St=st和 A t = a t A_t=a_t At=at是条件,意思是已经观测到 S t S_t St和 A t A_t At的值。条件期望的结果 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)被称为动作价值函数。
期望消除了随机变量 S t + 1 , A t + 1 , S t + 2 , A t + 2 , ⋯ , S n , A n S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_n,A_n St+1,At+1,St+2,At+2,⋯,Sn,An,因此动作价值函数 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)依赖于 s t s_t st和 a t a_t at,而不依赖于 t + 1 t+1 t+1时刻及其之后的状态和动作。由于动作 A t + 1 , A t + 2 , ⋯ , A n A_{t+1},A_{t+2},\cdots,A_n At+1,At+2,⋯,An的概率质量函数都是 π \pi π,因此使用不同的 π \pi π,求期望得到的结果就会有所不同,因此 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)还依赖于策略函数 π \pi π。
综上所述, t t t时刻的动作价值函数 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)依赖于以下三个因素:
- 当前状态 s t s_t st。当前状态越好,则 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)的值越大,也就是说回报的期望越大;
- 当前动作 a t a_t at。智能体执行的动作越好,则 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)的值越大;
- 策略函数 π \pi π。策略决定未来的动作 A t + 1 , A t + 2 , ⋯ , A n A_{t+1},A_{t+2},\cdots,A_n At+1,At+2,⋯,An的好坏,策略越好,则 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)的值越大。比如同样一局棋,柯洁(好的策略)来下,肯定会比我(差的策略)来下,得到的回报的期望会更大。
更准确地说, Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)应该叫做“动作状态价值函数”,但是一般习惯性地称之为“动作价值函数”。
3.2 状态价值函数(state-value function)
当阿尔法狗下棋时,它想知道当前状态 s t s_t st(即棋盘上的格局)是否对自己有利,以及自己和对手的胜算各有多大。这种用来量化双方胜算的函数就是状态价值函数。
将动作价值函数 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)中动作作为随机变量 A t A_t At,然后关于 A t A_t At求期望,把 A t A_t At消掉,即得到状态价值函数:
V π ( s t ) = E A t ∼ π ( ⋅ ∣ s t ) [ Q π ( s t ∣ , A t ) ] = ∑ a ∈ A π ( a ∣ s t ) ⋅ Q π ( s t , a ) ( 2 ) V_\pi(s_t)=\mathbb{E}_{A_t\sim\pi(\cdot|s_t)}[Q_\pi(s_t|,A_t)]=\displaystyle\sum_{a_\in\mathcal{A}}\pi(a|s_t)\cdot Q_\pi(s_t,a)~~~~~~~~~~~~~~~~~~~~~~~~~~~~(2) Vπ(st)=EAt∼π(⋅∣st)[Qπ(st∣,At)]=a∈A∑π(a∣st)⋅Qπ(st,a) (2)
状态价值函数 V π ( s t ) V_\pi(s_t) Vπ(st)只依赖于策略 π \pi π和当前状态 s t s_t st,不依赖于动作。状态价值函数 V π ( s t ) V_\pi(s_t) Vπ(st)也是回报 U t U_t Ut的期望, V π ( s t ) = E A t , S t + 1 , A t + 1 , ⋯ , S n , A n [ U t ∣ S t = s t ] V_\pi(s_t)=\mathbb{E}_{A_t,S_{t+1},A_{t+1},\cdots,S_n,A_n}[U_t|S_t=s_t] Vπ(st)=EAt,St+1,At+1,⋯,Sn,An[Ut∣St=st]。期望消掉了回报 U t U_t Ut依赖的随机变量 A t , S t + 1 , A t + 1 , ⋯ , S n , A n A_t,S_{t+1},A_{t+1},\cdots,S_n,A_n At,St+1,At+1,⋯,Sn,An,状态价值越大,则意味着回报的期望越大。用状态价值函数可以衡量策略 π \pi π与当前状态 s t s_t st的好坏。
4. 策略网络与价值网络
4.1 策略网络(policy network)
在围棋游戏中,动作空间 A = { 0 , 1 , 2 , ⋯ , 360 , 361 } \mathcal{A}=\{0,1,2,\cdots,360,361\} A={ 0,1,2,⋯,360,361}。策略函数 π \pi π是个条件概率质量函数:
π ( a ∣ s ) = △ P ( A = a ∣ S = s ) ( 3 ) \pi(a|s)\overset{\triangle}{=}\mathbb{P}(A=a|S=s)~~~~~~~~~~~~~~~~~~~~~~~~(3) π(a∣s)=△P(A=a∣S=s) (3)
策略函数 π \pi π的输入是状态 s s s和动作 a a a,输出是一个0到1之间的概率值,表示在状态 s s s的情况下,做出决策,从动作空间中选取动作 a a a的概率。
策略网络是用神经网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ)近似策略函数 π ( a ∣ s ) \pi(a|s) π(a∣s),其中 θ \theta θ表示神经网络的参数。一开始随机初始化 θ \theta θ,然后用收集到的状态、动作、奖励去更新 θ \theta θ。
策略网络的结构如图一所示。策略网络的输入是状态 s s s,在围棋游戏中,由于状态是张量,一般会使用卷积网络处理输入,生成特征向量。策略网络的输出层的激活函数是Softmax,因此输出的向量(记作 f f f)所有元素都是正数,而且相加等于1。向量 f f f的维度与动作空间 A \mathcal{A} A的大小相同,在围棋游戏中,动作空间 A \mathcal{A} A大小为362,因此向量 f f f就是一个362维的向量。
4.2 价值网络(value network)
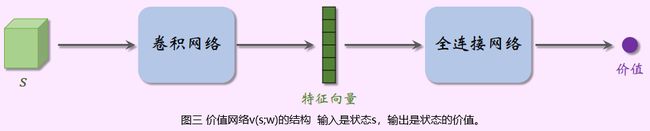
价值网络是用神经网络 q ( s , a ; ω ) q(s,a;\omega) q(s,a;ω)来近似动作价值函数 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)或用 v ( s ; θ ) v(s;\theta) v(s;θ)来近似状态价值函数 V π ( s ) V_\pi(s) Vπ(s),其中 ω \omega ω表示神经网络的参数。神经网络的结构是人为预先设定的,参数 ω \omega ω一开始随机初始化,并通过智能体与环境的交互来学习。
价值网络的结构如图二和图三所示。价值网络的输入是状态 s s s,在围棋游戏中,由于状态是一个张量,因此会使用卷积网络处理 s s s,生成特征向量。对于动作价值函数,价值网络输出每个动作的价值,动作空间 A \mathcal{A} A中有多少种动作,则价值网络的输出就是多少维的向量。对于状态价值函数,价值网络的输出是一个实数,表示状态的价值。
5. 蒙特卡洛(Monte Carlo)
蒙特卡洛是一大类通过随机样本估算真实值的随机算法(Randomized Algorithms)的总称,如通过实际观测值估算期望值、通过随机梯度近似目标函数关于神经网络参数的梯度。
价值网络的输出是回报 U t U_t Ut的期望。在强化学习中,可以将一局游戏进行到底,观测到所有的奖励 r 1 , r 2 , ⋯ , r n r_1,r_2,\cdots,r_n r1,r2,⋯,rn,然后计算出回报 u t = ∑ i = 0 n − t γ i r t + i u_t=\sum_{i=0}^{n-t}\gamma^ir_{t+i} ut=∑i=0n−tγirt+i。训练价值网络的时候以 u t u_t ut作为目标,这种方式即为“蒙特卡洛”。
原因非常显然:以动作价值函数为例,动作价值函数可以写作 Q π ( s t , a t ) = E [ U t ∣ S t = s t , A t = a t ] Q_\pi(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t] Qπ(st,at)=E[Ut∣St=st,At=at],而我们用实际观测 u t u_t ut去近似期望,这就是典型的蒙特卡洛近似。
蒙特卡洛的好处是无偏性: u t u_t ut是 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)的无偏估计。由于 u t u_t ut的无偏性,拿 u t u_t ut作为目标训练价值网络,得到的价值网络也是无偏的。
蒙特卡洛的坏处是方差大:随机变量 U t U_t Ut依赖于 S t + 1 , A t + 1 , ⋯ , S n , A n S_{t+1},A_{t+1},\cdots,S_n,A_n St+1,At+1,⋯,Sn,An这些随机变量,其中不确定性很大。观测值 u t u_t ut虽然是 U t U_t Ut的无偏估计,但可能实际上离 E [ U t ] \mathbb{E}[U_t] E[Ut]很远。因此拿 u t u_t ut作为目标训练价值网络,收敛会非常慢。
阿尔法狗的训练基于蒙特卡洛树搜索(后续文章会详细介绍),由于蒙特卡洛树搜索方差大的缺点,训练阿尔法狗的过程非常慢,据说DeepMind公司训练阿尔法狗用了5000块TPU?!
6. 结束语
机巧围棋核心AlphaGo Zero算法是一种深度强化学习算法,本文介绍了深度强化学习基础,相信通过本文能够让大家更好地理解后续文章中介绍的阿尔法狗算法原理。
最后,期待您能够给本文点个赞,同时去GitHub上给机巧围棋项目点个Star呀~
机巧围棋项目链接:https://github.com/QPT-Family/QPT-CleverGo