Acwing - 算法基础课 - 笔记（十四）

动态规划（三）

本节也是以例题讲解形式为主，主要包括了：数位统计DP，状态压缩DP，树形DP，记忆化搜索。

数位统计DP

计数问题

题目链接

给定两个数a和b，求解a和b之间的所有数字中0-9出现的次数。

比如a=10，b=13，则a和b之间共有4个数：

10，11，12，13

其中，0出现1次，1出现5次，2出现1次，3出现1次。

这道题更像是一道奥数问题，最重要的一步是：分情况讨论。

先考虑实现一个函数：count(n,x)，其表示在1到n中，x出现的次数（x是0-9）

那么，可以用类似前缀和的思想，来求解a到b中，x出现的次数：

count(b,x) - count(a-1,x)

那么先来看，求解count(n,1)，即1到n中，x=1出现的次数。

比如n是个7位的数字 abcdefg，我们可以分别求出1在每一位上出现的次数，然后做一个累加即可。

求1在第4位上出现的次数

即求解有多少个形如xxx1yyy的数字，恰好在1和abcdefg之间。

分情况讨论即可

• 当xxx取值是000到abc - 1之间，此时，第四位取1，后面3位yyy可以随便取（得到的数一定小于abcdefg）。

  即，当xxx = 000 ~ abc - 1时，yyy = 000 ~ 999

  一共是abc * 1000 种组合方式

• 当xxx恰好等于abc，此时又要分情况讨论

  • 当d < 1，此时abc1yyy > abc0efg，此时的次数是0
  • 当d = 1，此时yyy只能取000 ~ efg，此时次数为efg + 1
  • 当d > 1，此时abc1yyy，后面的yyy可以取任意值，即000 ~ 999，此时次数为1000

把上面全部的情况，累加起来，就是1出现在第四位的次数。

类似的，可以求解出1在任意一个位置上出现的次数，累加起来，就求出了1在每一位上出现的此时，即求解出了count(n,1)。

进一步，能够求解出count(n,x)

需要注意一下边界问题：当x=0时，不能有前导0，所以当x=0时，形如xxx0yyy，前面的xxx是从001到111，特别要注意前导0的 特判，当x=0时，循环不能从最高位开始，要从第二位开始。

（放在后面再讲，翻车了hhh）

这个题目可以看算法提高课数位DP章节的总结

#include 
#include 

using namespace std;

int a, b;

int power10(int x) {
     
	int res = 1;
	while(x--) res *= 10;
	return res;
}

int get(vector<int> v, int l, int r) {
     
	int res = 0;
	for(int i = l; i >= r; i--) res = res * 10 + v[i];
	return res;
}


// 求解在 1 - n 中 , x 出现的次数
int count(int n, int x) {
     
	if(n == 0) return 0;
	vector<int> v;
	while(n > 0) {
     
		v.push_back(n % 10);
		n /= 10;
	}
    n = v.size();
    
	int res = 0;
	// 若 x = 0, 则不能从第一位开始算
	for(int i = n - 1 - !x; i >= 0; i--) {
     
		if(i < n - 1) {
     
			res += get(v, n - 1, i + 1) * power10(i);
			if(x == 0) res -= power10(i); // x = 0 要减掉一种情况
		}
		if(x < v[i]) res += power10(i);
		else if(x == v[i]) res += get(v, i - 1, 0) + 1;
	}
	return res;
}

int main() {
     
	while(true) {
     
		scanf("%d%d", &a, &b);
		if(a == 0 && b == 0) break;
		if(a > b) swap(a, b);
		for(int i = 0; i <= 9; i++) {
     
			printf("%d ", count(b, i) - count(a - 1, i));
		}
		printf("\n");
	}
	return 0;
}

状态压缩DP

蒙德里安的梦想

题目链接

核心思路：先放横着的，再放竖着的。

总方案数，等于只放横着的小方块的合法方案数。（放完横着的方块之后，竖着的只能被动填充进去）

如何判断，当前方案是否合法？

方案合法的条件是：当横着的方块放完后，竖着的小方块恰好能把剩余的地方全部填满。

那如何判断方案是否合法呢？即怎么看竖着的小方块是否能把剩余部分填满呢？因为是竖着放的，所以可以按列来看，每一列的内部，只要所有连续的空余小方块的个数为偶数，即可。

这道题的f[i,j]比较难。

我们用f[i,j]表示，已经将前i-1列摆好，且从i-1列，伸出到第i列，状态是j，的所有方案。

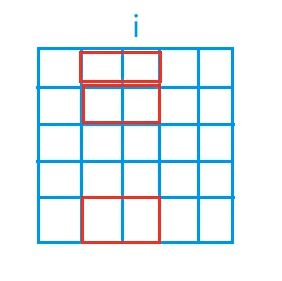
什么叫做，从第i-1列，伸出来到第i列呢，如下图，第i列的第1，2，5个格子，是从i-1列伸过来的。此时的状态j为 $11001_2$ ，即对于第i列的所有格子，第1，2，5个格子被伸出来占据了（j是个二进制数，若该列的某一行，有伸出来，则用1表示，否则用0表示）。

如上图所示，i = 2，j = 11001，此时的f[i,j]表示的就是，前i - 1列已经摆好，且从第i-1列，伸出到第i列的状态是j时，的全部方案数。（j用二进制来表示第i列的状态，但是我们写代码时，还是按照十进制的值来进行存储）。

这是一个化零为整的过程，因为前i-1列可以任意摆放，所以用f[i,j]一个状态，表示了很多种方案。

状态的表示搞定了，接下来是状态转换。

之前有说过，状态转换，通常是考虑最后一步的情况，根据最后一步的操作来进行分类，我们考虑f[i - 1][k]，即在i-1列的所有可能状态，f[i][j]一定是由某些f[i - 1][k]转移过来的，那k需要满足什么条件，才能够从f[i - 1][k]转移到f[i][j]呢？

首先，f[i - 1][k]，从i - 2列伸出到i - 1列的位置，不能和f[i][j]的那些伸出的位置冲突。如何判断这一点呢？由于是否伸出我们使用二进制位的1来表示，所以只需要对状态k和j做一下与操作，如果伸出的位置没有冲突，则j和k的所有二进制位中，不会在某一个位置，都是1的，即j & k 的结果等于0，就表明了k和j是不会冲突的。这是第一个条件。其次由于f[i][j]的含义中，包含了：前i - 1列已经全部摆好，所以第i - 1列已经是摆好了的，所以i - 1列剩余的连续空格子数，必须是偶数才行，那么此时i - 1列的状态是j | k，需要判断这个状态是否是合法的即可。

我们对于每个状态k，可以预处理出，这个状态的二进制表示中，所有连续0的个数是否是偶数（若所有连续0的个数是偶数，则我们称该状态为合法状态），我们用一个布尔数组st[k]来记录这个信息，当st[k] = true时，表示状态k是合法的。

最后的答案f[m,0]，列是从0到m-1。

化零为整：用一个f[i,j]来表示一堆方案

化整为零：对f[i,j]进行状态转移时，进行情况划分

代码如下：（朴素版）

#include 
#include 
using namespace std;

const int N = 12, M = 1 << N;

bool st[M]; // 存储状态是否合法, 当st[i] = true, 表示状态i合法, 合法的含义是: i的二进制表示, 连续0的个数都是偶数

long long f[N][M];

int n, m;

int main() {
     
	while(true) {
     
		scanf("%d%d", &n, &m);
		if(n == 0 && m == 0) break;

		// 预处理 st 数组
		for(int i = 0; i < 1 << n; i++) {
     
			st[i] = true;
			int cnt = 0; // 从二进制位的最低位开始统计连续0的个数
			for(int j = 0; j < n; j++) {
     
				if(i >> j & 1) {
      // 当前二进制位是1, 终止统计, 并判断此时连续0的个数
					if(cnt & 1) {
      // 连续0的个数为奇数, st[i]置为false, 并直接跳过后续计数
						st[i] = false;
						break;
					} // 若连续0的个数是偶数, 则继续进行下一轮计数, 此时cnt不需要清0, 不影响后续计数的
				} else cnt++; // 当前二进制位是0, 进行计数
			}
			if(cnt & 1) st[i] = false;  // 对最后一段连续0的个数的判断, 因为已经结束循环了
		}

		memset(f, 0, sizeof f);
		f[0][0] = 1; // 初始化, 从第-1列伸出到第0列, 且状态是0的方案数是 1
		for(int i = 1; i <= m; i++) {
      // 从第1列开始处理, 到第m列
			for(int j = 0; j < 1 << n; j++) {
      // 枚举第i列全部可能的状态, 从000...00, 到111...11
				for(int k = 0; k < 1 << n; k++) {
      // 枚举第 i-1列可能的状态k, 看能否从k转移到j
					if((j & k) == 0 && st[j | k]) {
      // 能够从k转移到j, 则方案数累加
						f[i][j] += f[i - 1][k];
					}
				}
			}
		}

		printf("%lld\n", f[m][0]);
	}
	return 0;
}

优化版：针对某一种状态j，我们可以预处理出有哪些合法状态k，可以从k转移到j

#include 
#include 
#include 
using namespace std;

const int N = 12, M = 1 << N;

bool st[M];

long long f[N][M];

int n, m;

vector<int> vs[M]; // 对于状态j, vs[j] 存储的是一个数组, 数组中每个元素, 都是能够转移到 j 的有效状态

int main() {
     
	while(true) {
     
		scanf("%d%d", &n, &m);
		if(n == 0 && m == 0) break;

		// 预处理
		for(int i = 0; i < 1 << n; i++) {
     
			st[i] = true;
			int cnt = 0;
			for(int j = 0; j < n; j++) {
     
				if(i >> j & 1) {
     
					if(cnt & 1) {
     
						st[i] = false;
						break;
					}
				} else cnt++;
			}
			if(cnt & 1) st[i] = false;
		}

		for(int i = 0; i < 1 << n; i++) {
     
			vs[i].clear(); //清除, 因为要重复使用
			for(int k = 0; k < 1 << n; k++) {
     
				if((i & k) == 0 && st[i | k]) vs[i].push_back(k);
			}
		}

		memset(f, 0, sizeof f);
		f[0][0] = 1;
		for(int i = 1; i <= m; i++) {
     
			for(int j = 0; j < 1 << n; j++) {
     
				for(auto k : vs[j]) {
      // 直接遍历有效状态, 进行累加即可
					f[i][j] += f[i - 1][k];
				}
			}
		}

		printf("%lld\n", f[m][0]);
	}
	return 0;
}

最短哈密顿路径

题目链接

这么简单的？？（视频课上yxc 10分钟就讲完+写完代码了）

// TODO

树形DP

没有上司的舞会

题目链接

状态转移方程大概说一下：

假设节点 $u$ 有 $N$ 个子节点，则

$f(u,0)={\sum }_1^{n}max\{f(s_i,0),f(s_i,1)\}$ ，由于0表示 $u$ 这个节点不选，则其每个子节点取最大值，即取 $max\{f(s,1),f(s,0)\}$，然后累加即可

而1 表示 $u$ 这个节点要选，则其子节点都不能选，所以

$f(u,1)=happ{y}_u+{\sum }_1^{n}f(s_i,0)$

用DFS+DP

#include 
#include 
using namespace std;

const int N = 6010;

int h[N], e[N], ne[N], idx; //图的邻接表存储

int happy[N];

bool has_father[N]; // 是否存在父节点, 用于找出树根

int n;

int f[N][2];

void add(int a, int b) {
     
    // 添加一条边 a -> b
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}

void dfs(int x) {
     
    // f[x][0] = 0, f[x][1] = happy[x]
	f[x][1] = happy[x];
	for(int i = h[x]; i != -1; i = ne[i]) {
     
		int u = e[i];
		dfs(u);
		f[x][0] += max(f[u][0], f[u][1]);
		f[x][1] += f[u][0];
	}
}

int main() {
     
	memset(h, -1, sizeof h);
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) scanf("%d", &happy[i]);

	for(int i = 0; i < n - 1; i++) {
     
		int a, b;
		scanf("%d%d", &a, &b);
		add(b, a); //b -> a , b为父节点, 表示上级
		has_father[a] = true;
	}

	// 找出树根
	int root;
	for(int i = 1; i <= n; i++) {
     
		if(!has_father[i]) {
     
			root = i;
			break;
		}
	}

	dfs(root);

	printf("%d\n", max(f[root][0], f[root][1]));

	return 0;
}

记忆化搜索

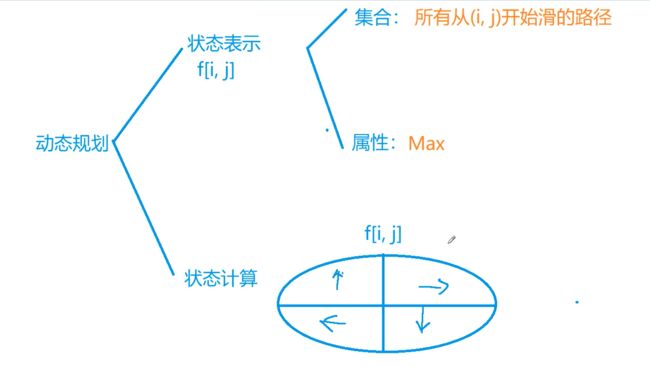
滑雪

题目链接

使用递归的方式来实现。

记忆化搜索的代码复杂度比较低，但是可能运行会慢一些些，然后如果递归深度比较深的话，可能会爆栈。

#include 
#include 
using namespace std;

const int N = 310;

int f[N][N];

int s[N][N];

int r, c;

int dx[4] = {
     1, -1, 0, 0};

int dy[4] = {
     0, 0, 1, -1};

int dp(int x, int y) {
     
	if(f[x][y] != -1) return f[x][y];
	int res = 1;
	for(int i = 0; i < 4; i++) {
     
		int nx = x + dx[i], ny = y + dy[i];
		// 滑过去的区域是有效的
		if(nx >= 1 && nx <= r && ny >= 1 && ny <= c && s[nx][ny] < s[x][y]) {
     
			res = max(res, dp(nx, ny) + 1);
		}
	}
	f[x][y] = res;
	return f[x][y];
}

int main() {
     
	memset(f, -1, sizeof f);
	scanf("%d%d", &r, &c);
	for(int i = 1; i <= r; i++) {
     
		for(int j = 1; j <= c; j++) scanf("%d", &s[i][j]);
	}

	int res = 1;
	for(int i = 1; i <= r; i++) {
     
		for(int j = 1; j <= c; j++) {
     
			res = max(res, dp(i, j));
		}
	}
	
	printf("%d\n", res);

	return 0;
}