【算法】解题总结：剑指 Offer 33 二叉搜索树的后序遍历序列、剑指 Offer 34 二叉树中和为某一值的路径

JZ33 二叉搜索树的后序遍历序列

（中等）

题目

描述
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。（ps：我们约定空树不是二叉搜索树）

示例
输入：
[4,8,6,12,16,14,10]
返回值：
true

思路

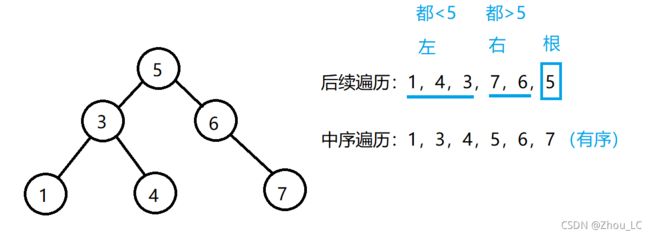
二叉搜索树由于其自身结构的特殊性，导致其在遍历时也有其独特的性质，二叉搜索树的中序遍历可以得到一个按结点值从小到大排序的有序序列；而在其后续遍历时，由于递归之中是先向左 dfs，再向右 dfs，最后才输出结点，因此，对于根结点来说，一定是最后才可以遍历到的，因此，对于本题给定的后续遍历结果，根结点的值一定是序列的最后一个元素的值，而又由于在二叉搜索树中，根结点的左子树一定都小于根结点的值，而根结点的右子树一定都大于根结点的值，且一定是先遍历完左子树的那批结点，再遍历右子树的那批结点。

因此，我们可以在本题的给定序列中，找到左子树的那一批子序列与右子树的那一批子序列，如果左子树序列都小于根结点的值，即最后一个元素的值，而右子树序列都大于根结点的值，那么再进一步递归左右子序列，将其作为一颗新的二叉搜索树来判断，最终如果start >= end，也就是递归序列的起始下标大于等于终止下标，则返回 true，在历经不断的方法栈探出，递归最终结束，如果期间为返回过 false，则最终结果为 true，反之为 false。

实现

public class JZ33二叉搜索树的后序遍历序列 {
     
    int[] mySequence = null;

    public boolean VerifySquenceOfBST(int [] sequence) {
     
        if (sequence == null || sequence.length == 0) {
     
            return false;
        }

        mySequence = sequence;

        return isPostOrder(0, sequence.length - 1);
    }

    public boolean isPostOrder(int start, int end) {
     
        if (start >= end) {
     
            return true;
        }

        //最后一个元素值为根结点的元素值，即 mySequence[end]

        //首先要确定左子树部分的范围，左子树结点值都要小于 mySequence[end]
        int mid = start;
        while (mySequence[mid] < mySequence[end]) {
     mid++;}
        //mid此时指向右子树的起始下标，右子树的都要大于 mySequence[end]
        for (int i = mid; i < end; i++) {
     
            if (mySequence[i] < mySequence[end]) {
     
                return false;
            }
        }

        return isPostOrder(start, mid - 1) && isPostOrder(mid, end - 1);
    }
}

JZ34 二叉树中和为某一值的路径

（中等）

题目

描述
输入一颗二叉树的根节点root和一个整数expectNumber，找出二叉树中结点值的和为expectNumber的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
如二叉树root为{10,5,12,4,7},expectNumber为22

则合法路径有[[10,5,7],[10,12]]
数据范围:
树中节点总数在范围 [0, 5000] 内
-1000 <= 节点值 <= 1000
-1000 <= expectNumber <= 1000

示例1
输入：
{10,5,12,4,7},22
返回值：
[[10,5,7],[10,12]]
说明：
返回[[10,12],[10,5,7]]也是对的

示例2
输入：
{10,5,12,4,7},15
返回值：
[]

示例3
输入：
{5,4,8,11,#,13,4,7,2,#,#,5,1},22
返回值：
[[5,4,11,2],[5,8,4,5]]

思路

本题思路为借助一个临时数组来进行递归与回溯时临时结果路径的保存，前序遍历树结构，最终统计所有这样符合条件的路径数组。

而题目对于符合条件的路径数组的要求为，路径上结点值的和等于给定参数 expectNumber，我们在每次递归遍历或是回溯时，为了避免统计之前结点值与删除之前结点值时的繁琐操作，直接在每次递归时，用 expectNumber 减去当前结点的值，从而每次只参考剩余需要的值，这样无论是递归或是回溯时，我们思考起来都非常得思路清晰。题目中有一处要求 “路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径” ，因此，路径都是最终要到叶子结点并且符合条件才算数，所以，找到一条路径的条件为 node.left == null && node.right == null && remainNum == node.val，这时要记录下此路径，也要删除当前结点值，从而在回溯后进行一条新路径的判断，而整个前序遍历的递归，在开始时为了进行判断，要加入当前结点值到临时数组中，在结束时，也就是左右递归方法都弹出栈时，也要将当前结点值在临时数组中删除，因此此结点已在之前的左右递归方法中都已判断过。

实现

public class JZ34二叉树中和为某一值的路径 {
     
    ArrayList<ArrayList<Integer>> allList = new ArrayList();
    ArrayList<Integer> oneList = new ArrayList();

    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root, int expectNumber) {
     
        if (root == null) return allList;

        backtrackTraversal(root, expectNumber);
        return allList;
    }

    public void backtrackTraversal(TreeNode node, int remainNum) {
     
        if (node == null) return;

        oneList.add(node.val);

        if (node.left == null && node.right == null && remainNum == node.val) {
     
            allList.add(new ArrayList(oneList));
            oneList.remove(oneList.size() - 1);
            return;
        }

        backtrackTraversal(node.left, remainNum - node.val);
        backtrackTraversal(node.right, remainNum - node.val);
        oneList.remove(oneList.size() - 1);
    }
}