Alink漫谈(十四) :多层感知机 之 总体架构
Alink漫谈(十四) :多层感知机 之 总体架构
文章目录
- Alink漫谈(十四) :多层感知机 之 总体架构
-
- 0x00 摘要
- 0x01 背景概念
-
- 1.1 前馈神经网络
- 1.2 反向传播
- 1.3 代价函数
- 1.4 优化过程
-
- 1.4.1 迭代法
- 1.4.2 梯度下降
- 1.5 相关公式
-
- 1.5.1 加权求和 h
- 1.5.2 神经元输出值 a
- 1.5.3 输出层的输出值 y
- 1.5.4 激活函数g(h)
- 1.5.5 损失函数E
- 1.5.6 误差反向传播——更新权重
- 1.5.7 输出层增量项 δo
- 1.5.8 更新输出层权重wjk
- 0x02 示例代码
- 0x03 训练总体逻辑
-
- 3.1 总体逻辑示例图
- 3.2 L-BFGS训练调用逻辑概述
- 3.3 获取训练数据
- 3.4 构建拓扑
-
- 3.4.1 AffineLayer
- 3.4.2 FuntionalLayer
- 3.4.3 SoftmaxLayerWithCrossEntropyLoss
-
- 3.4.3.1 Softmax
- 3.4.3.2 softmax loss
- 3.4.3.3 cross entropy
- 3.4.3.4 SoftmaxLayerWithCrossEntropyLoss
- 3.5 构建训练器
- 0xFF 参考
0x00 摘要
Alink 是阿里巴巴基于实时计算引擎 Flink 研发的新一代机器学习算法平台,是业界首个同时支持批式算法、流式算法的机器学习平台。本文和下文将带领大家来分析Alink中多层感知机的实现。
因为Alink的公开资料太少,所以以下均为自行揣测,肯定会有疏漏错误,希望大家指出,我会随时更新。
0x01 背景概念
几乎所有的深度学习算法都可以被描述为一个相当简单的配方:特定的数据集、代价函数、优化过程和模型。
1.1 前馈神经网络
前馈神经网络(Feedforward Neural Network, FNN )中,把每个神经元按接收信息的先后分为不同的组,每一组可以看做是一个神经层。每一层中的神经元接收前一层神经元的输出,并输出到下一层神经元。整个网络中的信息是朝着一个方向传播的,没有反向的信息传播(和误差反向传播不是一回事),即整个网络中无反馈,信号从输入层向输出层单向传播,可以用一个有向无环图来表示。在前馈神经网络中,第0层叫做输入层,最后一层叫做输出层,其他中间层叫做隐藏层。
反馈神经网络中神经元不但可以接收其他神经元的信号,而且可以接收自己的反馈信号。和前馈神经网络相比,反馈神经网络中的神经元具有记忆功能,在不同时刻具有不同的状态。反馈神经网络中的信息传播可以是单向也可以是双向传播,因此可以用一个有向循环图或者无向图来表示。
前馈网络的主要目标是近似一些函数f*。例如,回归函数y = f *(x)将输入x映射到值y。前馈网络定义了y = f (x; θ)映射,并学习参数θ的值,使结果更加接近最佳函数。
例如,我们有三个函数f(1),f(2)和f(3)连接在一个链上以形成f(x)=f(3)(f(2)(f(1)(x)))。这些链式结构是神经网络中最常用的结构。在这种情况下,f(1)被称为网络的第一层(first layer),f(2)被称为第二层(second layer),依此类推。链的全长称为模型的深度(depth)。正是因为这个术语才出现了”深度学习”这个名字。
现在问题来了,为什么当我们有线性机器学习模型时,还需要前馈网络?这是因为线性模型仅限于线性函数,而神经网络不是。当我们的数据不是线性可分离的线性模型时,面临着近似的问题,而神经网络则相当容易应对。隐藏层用于增加非线性并改变数据的表示,以便更好地泛化函数。
1.2 反向传播
怎么理解这个“反向传播”呢,其实DL的核心理念就在于找到全局性误差函数Loss符合要求的,对应的权值 “w” 与 “b”。那么问题就来了,当得到的误差Loss不符合要求(即误差过大),就可以通过“反向传播”的方式,把输出层得到的误差反过来传到隐含层,并分配给不同的神经元,以此调整每个神经元的“权值”,最终调整至Loss符合要求为止,这就是“误差反响传播”的核心理念。
在此我们首先要澄清一个容易混淆的概念,即有的地方经常会用反向传播来代指深度模型的整个学习算法,其实这是不准确的,整体的学习算法可以分为两方面:
- 代价信息如何传递到深度模型的每一层?
- 基于传递到本层的信息,本层的参数应该如何更新?
在特定结构中,信息沿着组织结构向前流动,我们称之为前向传播,相应的,反向传播则指信息沿着结构从后向前流动。
在前馈神经网络中,前向传播的是输入,并且在过程中逐渐抽象为特征,反向传播的则是当前输出值与期望输出的代价信息,或者说误差,传递到每一层的信息则是该层的输出值与该层的 “期望输出” 的代价信息。
在如今的主流框架中,反向传播与代价信息和梯度结合起来借助计算图来实现。因此,反向传播既不是只有神经网络或者深度模型才有,也不能全部代表深度模型的整个学习算法,它所代表的只是第一个问题,即基于代价信息如何更新参数如何进行更高效的优化则是优化算法的问题。现代最有效的优化算法主要是基于梯度下降的,并以其为基础做出了很多创新工作。
总结深度模型的训练过程如下:针对既定的网络结构和性能指标,细致地定义代价/误差/目标函数,输入通过前向传播到达输出层,并且针对每一个或一批输入产生的输出,在定义好的代价函数下计算代价信息,通过反向传播传递到深度模型的每一层,在每一层上基于代价信息对参数的梯度更新参数,直到满足停止条件,完成训练。
1.3 代价函数
代价函数的作用是显示了我们的模型得出的近似值与我们试图达到的实际目标值之间的差异。
通常代价函数至少含有一项使学习过程进行统计估计的成分。最常见的代价函数是负对数似然、最小化代价函数导致的最大似然估计。代价函数也可能含有附加项,如正则化项。
在某些情况下,由于计算原因,我们不能实际计算代价函数。在这种情况下,只要我们有近似其梯度的方法,那么我们仍然可以使用迭代数值优化近似最小化目标。
与机器学习算法一样,前馈网络也使用基于梯度的学习方法进行训练,在这种学习方法中,使用随机梯度下降等算法来使代价函数达到最小化。整个训练过程在很大程度上取决于我们的代价函数的选择,其选择或多或少与其他参数模型相同。
对于反向传播算法的代价函数,它必须满足两个属性:
-
代价函数必须能够表达为平均值。
-
代价函数不能依赖于输出层旁边网络的任何激活值。
代价函数的形式主要是C(W, B, Sr, Er),其中W是神经网络的权重,B是网络的偏置,Sr是单个训练样本的输入,Er是该训练样本的期望输出。
1.4 优化过程
1.4.1 迭代法
在一个算法模型训练最开始,权值w和偏置b都是随机赋予的,理论上它可能是出现在整个函数图像中的任何位置,那如何让他去找到我们所要求的那个值呢。
这里就要引入“迭代”的思想:我们可以通过代入左右不同的点去尝试,假设代入当前 x 左面的一个点比右面的更小,那么就可以让 x 变为左面的点,然后继续尝试,直到找到“极小值”么。这也是为什么算法模型需要时间去不断迭代很训练的原因。
1.4.2 梯度下降
使用迭代法,那么随之而来另外一个问题:这样一个一个尝试,虽然最终结果是一定会找到我们所需要的值,但有没有什么方法可以让它离“极值”远的时候,挪动的步子更大,离“极值”近的时候,挪动的步子变小(防止越过极值),实现更快更准确地“收敛”。假如是一个“二次函数”的图像,那么如果取得点越接近“极小值”,在这个点的函数“偏导”越小(偏导即“在那个点的函数斜率”)。接下来引出下面这个方法:
x n + 1 = x n − η d f ( x ) d x x_{n+1} = x_n - η\frac{df(x)}{dx} xn+1=xn−ηdxdf(x)
梯度下降核心思想:Xn代表的就是挪动的“步长”,后面的部分表示当前这个点在函数的“偏导”,这样也就代表当点越接近极值点,那么“偏导”越小,所以挪动的“步长”就短;反之如果离极值点很远,则下一次挪动的“步长”越大。
把这个公式换到我们的算法模型,就找到了“挪动步长”与Loss和(w,b)之间的关系,实现快速“收敛”。
通过“迭代法”和“梯度下降法”的配合,我们实现了一轮一轮地迭代,每次更新都会越来越接近极值点,直到更新的值非常小或已经满足我们的误差范围内,训练结束,此时得到的(w,b)就是我们寻找的模型。
1.5 相关公式
以下是相关各种公式,摘录出来给大家在阅读时查阅。
1.5.1 加权求和 h
h j = ∑ i = 0 M w i j x j h_j = \sum_{i=0}^M w_{ij}x_j hj=i=0∑Mwijxj
hj 表示当前节点的所有输入加权之和。
1.5.2 神经元输出值 a
a j = g ( h j ) = g ( ∑ i = 0 M w i j x j ) a_j = g(h_j) = g(\sum_{i=0}^M w_{ij}x_j) aj=g(hj)=g(i=0∑Mwijxj)
- a_j 表示隐藏层神经元的输出值。
- g()代表激活函数,w是权重,x是输入。
- a_j=x_jk 即当前层神经元的输出值,等于下一层神经元的输入值。
1.5.3 输出层的输出值 y
y = a k = g ( h k ) = g ( ∑ i = 0 M w j k x j k ) y = a_k = g(h_k) = g(\sum_{i=0}^M w_{jk}x_{jk}) y=ak=g(hk)=g(i=0∑Mwjkxjk)
- y 表示输出层的值,也就是最终结果。
- h_k 表示输出层神经元k的输入加权之和。
1.5.4 激活函数g(h)
采用Sigmoid function:
g ( h ) = σ ( h ) = 1 1 + e − h g(h)=σ(h)= \frac{1}{1+e^{-h}} g(h)=σ(h)=1+e−h1
sigmoid函数的导数:
σ ′ ( x ) = σ ( x ) [ 1 − σ ( x ) ] σ ′(x)=σ(x)[1−σ(x)] σ′(x)=σ(x)[1−σ(x)]
将 aj=g(hj) 代入可得
g ′ ( h ) = a j ( 1 − a j ) g ′ (h)=a_j (1−a_j ) g′(h)=aj(1−aj)
1.5.5 损失函数E
采用误差平方和(sum-of-squares error function)
E = 1 2 ∑ k = 1 N ( y − t ) 2 E = \frac{1}{2}\sum _{k=1}^N(y-t)^2 E=21k=1∑N(y−t)2
- 平方是为了避免超平面两端的误差点相互抵消(y−t 存在正负)。
- 前面系数取1/2 是为了之后采用梯度下降时,求梯度(偏导数)时能抵消平方求导后的2。
1.5.6 误差反向传播——更新权重
采用梯度下降求最优解,也就是求损失函数E关于权重w的偏导数
∂ E ∂ w i k = ∂ E ∂ h k ∂ h k ∂ w i k \frac{∂E}{∂w_{ik}} = \frac{∂E}{∂h_k} \frac{∂h_k}{∂w_{ik}} ∂wik∂E=∂hk∂E∂wik∂hk
等式右边可以解释为:如果我们想知道当权重w改变时,输出的误差E是如何变化的,我们可以通过观察误差E是如何随着激活函数的输入值h变化,以及激活函数的输入值h是如何随着权重w变化。
h_k表示输出层神经元k的所有输入加权之和,也就是激活函数g(h)的输入值。
1.5.7 输出层增量项 δo
右边第一项比较重要,这里称为增量项δ(error or delta term),继续通过链式法则推导,最终得到输出层的增量项
δ o ( k ) = ∂ E ∂ h k = ∂ E ∂ y ∂ y ∂ h k = ( y − t ) g ′ ( h k ) δ_o(k) = \frac{∂E}{∂h_{k}} = \frac{∂E}{∂y} \frac{∂y}{∂h_k} = (y−t)g ′(h_ k ) δo(k)=∂hk∂E=∂y∂E∂hk∂y=(y−t)g′(hk)
接下来可以对输出层的权重w进行更新。
1.5.8 更新输出层权重wjk
对损失函数使用梯度下降法,更新权重:
w j k ← w j k − η ∂ E ∂ w j k w_{jk} ←w _{jk} −η \frac{∂E}{∂w_{jk}} wjk←wjk−η∂wjk∂E
于是得到
w j k = w j k − η δ o ( k ) a i w_{jk} = w_{jk} - ηδ_o(k)a_i wjk=wjk−ηδo(k)ai
ai是上一层的输出值,也即是输出层的输入值xi。
0x02 示例代码
本文示例代码如下:
public class MultilayerPerceptronClassifierExample {
public static void main(String[] args) throws Exception {
BatchOperator data = Iris.getBatchData();
MultilayerPerceptronClassifier classifier = new MultilayerPerceptronClassifier()
.setFeatureCols(Iris.getFeatureColNames())
.setLabelCol(Iris.getLabelColName())
.setLayers(new int[]{
4, 5, 3})
.setMaxIter(100)
.setPredictionCol("pred_label")
.setPredictionDetailCol("pred_detail");
BatchOperator res = classifier.fit(data).transform(data);
res.print();
}
}
Iris定义如下
public class Iris {
final static String URL = "https://alink-release.oss-cn-beijing.aliyuncs.com/data-files/iris.csv";
final static String SCHEMA_STR
= "sepal_length double, sepal_width double, petal_length double, petal_width double, category string";
public static BatchOperator getBatchData() {
return new CsvSourceBatchOp(URL, SCHEMA_STR);
}
public static StreamOperator getStreamData() {
return new CsvSourceStreamOp(URL, SCHEMA_STR);
}
public static String getLabelColName() {
return "category";
}
public static String[] getFeatureColNames() {
return new String[] {
"sepal_length", "sepal_width", "petal_length", "petal_width"};
}
}
0x03 训练总体逻辑
MultilayerPerceptronTrainBatchOp 类是批处理训练的实现。
protected BatchOperator train(BatchOperator in) {
return new MultilayerPerceptronTrainBatchOp(this.getParams()).linkFrom(in);
}
所以还是老套路,直接看 MultilayerPerceptronTrainBatchOp 的 linkFrom 函数。
其大致思路如下:
- 1)获取一些元信息,比如label名称,特征列名,特征类型等;
- 2)获取测试数据
trainData = getTrainingSamples; - 3)训练
- 3.1)获取初始权重
initialWeights = getInitialWeights(); - 3.2)构建拓扑
topology = FeedForwardTopology.multiLayerPerceptron - 3.3)构建训练器
FeedForwardTrainer。- 3.3.1)初始化模型
- 3.3.2)构建目标函数
- 3.3.3)训练器会基于目标函数构建优化器,这里的优化器是
L-BFGS。
- 3.4)训练获取最终权重
weights = trainer.train
- 3.1)获取初始权重
- 4)输出模型
DataSet;
- 5)把
DataSet转成Table;
@Override
public MultilayerPerceptronTrainBatchOp linkFrom(BatchOperator<?>... inputs) {
BatchOperator<?> in = checkAndGetFirst(inputs);
// 1)获取一些元信息,比如label名称,特征列名,特征类型等。
final String labelColName = getLabelCol();
final String vectorColName = getVectorCol();
final boolean isVectorInput = !StringUtils.isNullOrWhitespaceOnly(vectorColName);
final String[] featureColNames = isVectorInput ? null :
(getParams().contains(FEATURE_COLS) ? getFeatureCols() :
TableUtil.getNumericCols(in.getSchema(), new String[]{
labelColName}));
final TypeInformation<?> labelType = in.getColTypes()[TableUtil.findColIndex(in.getColNames(),
labelColName)];
DataSet<Tuple2<Long, Object>> labels = getDistinctLabels(in, labelColName);
// 此处程序变量如下:
labelColName = "category"
vectorColName = null
isVectorInput = false
featureColNames = {
String[4]@6412}
0 = "sepal_length"
1 = "sepal_width"
2 = "petal_length"
3 = "petal_width"
labelType = {
BasicTypeInfo@6414} "String"
labels = {
MapOperator@6415}
// 2)获取测试数据
// get train data
DataSet<Tuple2<Double, DenseVector>> trainData =
getTrainingSamples(in, labels, featureColNames, vectorColName, labelColName);
// train 3)训练
final int[] layerSize = getLayers();
final int blockSize = getBlockSize();
// 3.1)获取初始权重
final DenseVector initialWeights = getInitialWeights();
// 3.2)获取拓扑
Topology topology = FeedForwardTopology.multiLayerPerceptron(layerSize, true);
// 3.3)构建训练器
FeedForwardTrainer trainer = new FeedForwardTrainer(topology,
layerSize[0], layerSize[layerSize.length - 1], true, blockSize, initialWeights);
// 3.4)训练获取最终权重
DataSet<DenseVector> weights = trainer.train(trainData, getParams());
// output model 4)输出模型
DataSet<Row> modelRows = weights
.flatMap(new RichFlatMapFunction<DenseVector, Row>() {
@Override
public void flatMap(DenseVector value, Collector<Row> out) throws Exception {
List<Tuple2<Long, Object>> bcLabels = getRuntimeContext().getBroadcastVariable("labels");
Object[] labels = new Object[bcLabels.size()];
bcLabels.forEach(t2 -> {
labels[t2.f0.intValue()] = t2.f1;
});
MlpcModelData model = new MlpcModelData(labelType);
model.labels = Arrays.asList(labels);
model.meta.set(ModelParamName.IS_VECTOR_INPUT, isVectorInput);
model.meta.set(MultilayerPerceptronTrainParams.LAYERS, layerSize);
model.meta.set(MultilayerPerceptronTrainParams.VECTOR_COL, vectorColName);
model.meta.set(MultilayerPerceptronTrainParams.FEATURE_COLS, featureColNames);
model.weights = value;
new MlpcModelDataConverter(labelType).save(model, out);
}
})
.withBroadcastSet(labels, "labels");
// 5)把DataSet转成Table
setOutput(modelRows, new MlpcModelDataConverter(labelType).getModelSchema());
}
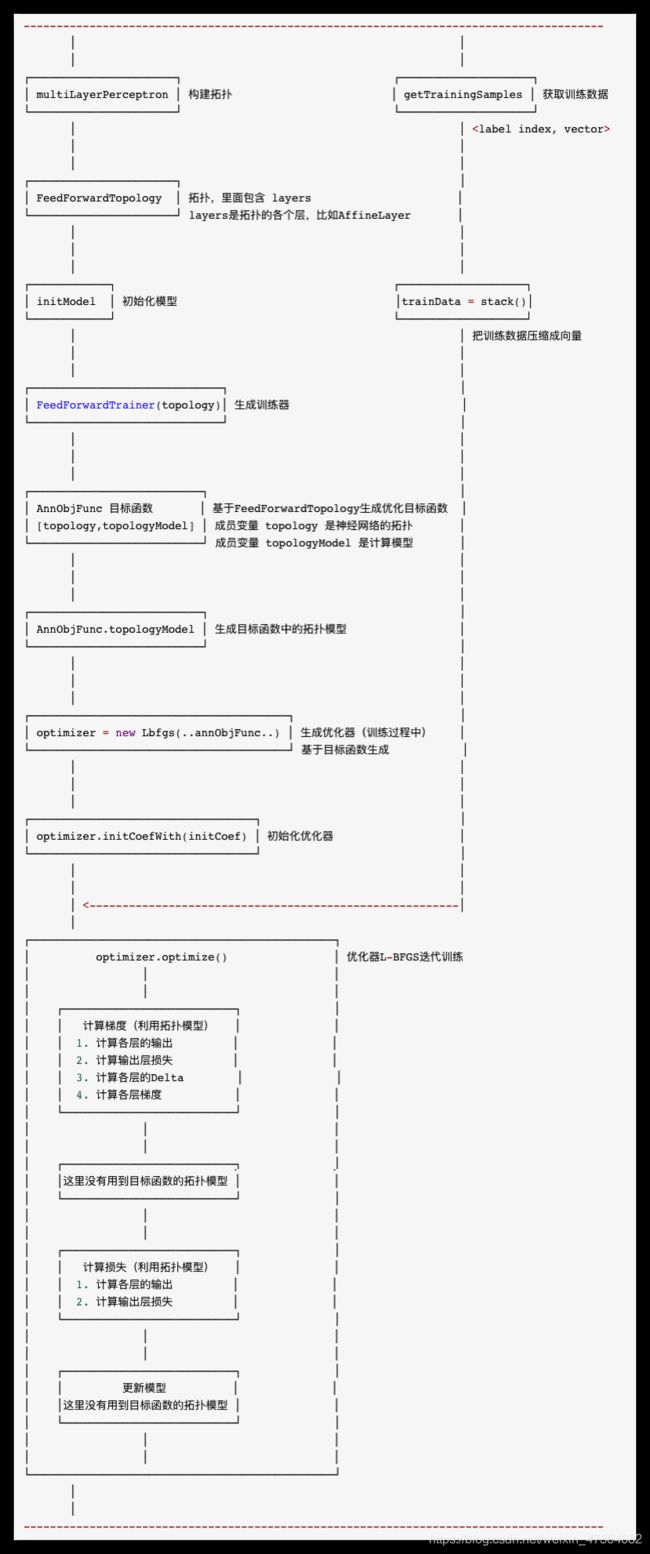
3.1 总体逻辑示例图
总体逻辑示例图如下,这里为了更好说明,把初始化步骤顺序做了微调。
----------------------------------------------------------------------------------------
│ │
│ │
┌──────────────────────┐ ┌────────────────────┐
│ multiLayerPerceptron │ 构建拓扑 │ getTrainingSamples │ 获取训练数据
└──────────────────────┘ └────────────────────┘
│ │ <label index, vector>
│ │
│ │
┌──────────────────────┐ │
│ FeedForwardTopology │ 拓扑,里面包含 layers │
└──────────────────────┘ layers是拓扑的各个层,比如AffineLayer │
│ │
│ │
│ │
┌────────────┐ ┌────────────────────┐
│ initModel │ 初始化模型 │trainData = stack() │
└────────────┘ └────────────────────┘
│ │ 把训练数据压缩成向量
│ │
│ │
┌─────────────────────────────┐ │
│ FeedForwardTrainer(topology)│ 生成训练器 │
└─────────────────────────────┘ │
│ │
│ │
│ │
┌──────────────────────────┐ │
│ AnnObjFunc 目标函数 │ 基于FeedForwardTopology生成优化目标函数 │
│ [topology,topologyModel] │ 成员变量 topology 是神经网络的拓扑 │
└──────────────────────────┘ 成员变量 topologyModel 是计算模型 │
│ │
│ │
│ │
┌──────────────────────────┐ │
│ AnnObjFunc.topologyModel │ 生成目标函数中的拓扑模型 │
└──────────────────────────┘ │
│ │
│ │
│ │
┌───────────────────────────────────────┐ │
│ optimizer = new Lbfgs(..annObjFunc..) │ 生成优化器(训练过程中) │
└───────────────────────────────────────┘ 基于目标函数生成 │
│ │
│ │
│ │
┌──────────────────────────────────┐ │
│ optimizer.initCoefWith(initCoef) │ 初始化优化器 │
└──────────────────────────────────┘ │
│ │
│ │
│ <--------------------------------------------------------│
│
┌──────────────────────────────────────────────┐
│ optimizer.optimize() │ 优化器L-BFGS迭代训练
│ │ │
│ │ │
│ ┌──────────────────────────┐ │
│ │ 计算梯度(利用拓扑模型) │ │
│ │ 1. 计算各层的输出 │ │
│ │ 2. 计算输出层损失 │ │
│ │ 3. 计算各层的Delta │ │
│ │ 4. 计算各层梯度 │ │
│ └──────────────────────────┘ │
│ │ │
│ │ │
│ ┌──────────────────────────┐ │
│ │ 计算方向 │ │
│ │这里没有用到目标函数的拓扑模型 │ │
│ └──────────────────────────┘ │
│ │ │
│ │ │
│ ┌──────────────────────────┐ │
│ │ 计算损失(利用拓扑模型) │ │
│ │ 1. 计算各层的输出 │ │
│ │ 2. 计算输出层损失 │ │
│ └──────────────────────────┘ │
│ │ │
│ │ │
│ ┌──────────────────────────┐ │
│ │ 更新模型 │ │
│ │这里没有用到目标函数的拓扑模型 │ │
│ └──────────────────────────┘ │
│ │ │
│ │ │
└──────────────────────────────────────────────┘
│
│
----------------------------------------------------------------------------------------
上面图可能在手机上变形,所以也可以参见下面图片:
3.2 L-BFGS训练调用逻辑概述
针对上图需要说明,L-BFGS是我们的优化器,其中几个关键步骤如下:
CalcGradient()计算梯度CalDirection(...)计算方向CalcLosses(...)计算损失UpdateModel(...)更新模型
算法框架都是基本不变的,所差别的就是具体目标函数和损失函数的不同。比如线性回归采用的是UnaryLossObjFunc,损失函数是 SquareLossFunc。而多层感知机这里,用的目标函数是:AnnObjFunc。
具体针对多层感知机,L-BFGS中 与目标函数 的相关步骤如下:
CalcGradient 计算梯度
- 1)调用
AnnObjFunc.updateGradient;- 1.1)调用 目标函数中拓扑模型
topologyModel.computeGradient来计算- 1.1.1)计算各层的输出;
forward(data, true) - 1.1.2)计算输出层损失;
labelWithError.loss - 1.1.3)计算各层的Delta;
layerModels.get(i).computePrevDelta - 1.1.4)计算各层梯度;
layerModels.get(i).grad
- 1.1.1)计算各层的输出;
- 1.1)调用 目标函数中拓扑模型
CalDirection 计算方向
- 这里没有用到目标函数的拓扑模型。
CalcLosses 计算损失
- 1)调用
AnnObjFunc.calcSearchValues;其内部会调用calcLoss计算损失;- 1.1)调用
topologyModel.computeGradient来计算损失- 1.1.1)计算各层的输出;
forward(data, true) - 1.1.2)计算输出层损失;
labelWithError.loss
- 1.1.1)计算各层的输出;
- 1.1)调用
UpdateModel 更新模型
- 这里没有用到目标函数的拓扑模型。
3.3 获取训练数据
getTrainingSamples函数将从原始输入获取训练数据。
原始数据举例
5.1 3.5 1.4 0.2 Iris-setosa
5 2 3.5 1 Iris-versicolor
5.1 3.7 1.5 0.4 Iris-setosa
6.4 2.8 5.6 2.2 Iris-virginica
6 2.9 4.5 1.5 Iris-versicolor
主要做了如下:
- 1)获取元数据,比如特征列的index,label列的index;
- 2)把labels广播,后续会在open函数中使用;
- 3)open函数中得倒一个
label : index的映射 - 4)map 函数中有两种执行序列,都会转换为
这样的二元组- 4.1)原始输入中有vector,比如类似 5.1 3.5 1.4 0.2 Iris-setosa 5.1 3.5 1.4 0.2,这些加粗的就是vector。
- 4.2)原始输入中没有vector,比如类似 5.1 3.5 1.4 0.2 Iris-setosa ;
具体代码如下:
private static DataSet<Tuple2<Double, DenseVector>> getTrainingSamples(
BatchOperator data, DataSet<Tuple2<Long, Object>> labels,
final String[] featureColNames, final String vectorColName, final String labelColName) {
// 1)获取元数据,比如特征列的index,label列的index;
final boolean isVectorInput = !StringUtils.isNullOrWhitespaceOnly(vectorColName);
final int vectorColIdx = isVectorInput ? TableUtil.findColIndex(data.getColNames(), vectorColName) : -1;
final int[] featureColIdx = isVectorInput ? null : TableUtil.findColIndices(data.getSchema(),
featureColNames);
final int labelColIdx = TableUtil.findColIndex(data.getColNames(), labelColName);
// 程序变量如下
isVectorInput = false
vectorColIdx = -1
featureColIdx = {
int[4]@6443}
0 = 0
1 = 1
2 = 2
3 = 3
labelColIdx = 4
DataSet<Row> dataRows = data.getDataSet();
return dataRows
.map(new RichMapFunction<Row, Tuple2<Double, DenseVector>>() {
transient Map<Comparable, Long> label2index;
@Override
public void open(Configuration parameters) throws Exception {
List<Tuple2<Long, Object>> bcLabels = getRuntimeContext().getBroadcastVariable("labels");
this.label2index = new HashMap<>();
// 得倒一个label : index 的映射
bcLabels.forEach(t2 -> {
Long index = t2.f0;
Comparable label = (Comparable) t2.f1;
this.label2index.put(label, index);
});
// 变量是
this = {
MultilayerPerceptronTrainBatchOp$2@11578}
label2index = {
HashMap@11580} size = 3
"Iris-versicolor" -> {
Long@11590} 2
"Iris-virginica" -> {
Long@11592} 1
"Iris-setosa" -> {
Long@11594} 0
}
@Override
public Tuple2<Double, DenseVector> map(Row value) throws Exception {
Comparable label = (Comparable) value.getField(labelColIdx);
Long labelIdx = this.label2index.get(label);
if (isVectorInput) {
// 4.1)如果原始输入中有vector
Vector vec = VectorUtil.getVector(value.getField(vectorColIdx));
// 转换为
if (null == vec) {
return new Tuple2<>(labelIdx.doubleValue(), null);
} else {
return new Tuple2<>(labelIdx.doubleValue(),
(vec instanceof DenseVector) ? (DenseVector) vec
: ((SparseVector) vec).toDenseVector());
}
} else {
// 4.2)如果原始输入中没有vector
int n = featureColIdx.length;
DenseVector features = new DenseVector(n);
for (int i = 0; i < n; i++) {
double v = ((Number) value.getField(featureColIdx[i])).doubleValue();
features.set(i, v);
}
// 转换为
return Tuple2.of(labelIdx.doubleValue(), features);
}
}
})
.withBroadcastSet(labels, "labels"); // 2)把labels广播,在open函数中使用;
}
3.4 构建拓扑
FeedForwardTopology.multiLayerPerceptron 完成了构建前馈神经网络拓扑的工作。
public static FeedForwardTopology multiLayerPerceptron(int[] layerSize, boolean softmaxOnTop) {
List<Layer> layers = new ArrayList<>((layerSize.length - 1) * 2);
for (int i = 0; i < layerSize.length - 1; i++) {
layers.add(new AffineLayer(layerSize[i], layerSize[i + 1]));
if (i == layerSize.length - 2) {
if (softmaxOnTop) {
layers.add(new SoftmaxLayerWithCrossEntropyLoss());
} else {
layers.add(new SigmoidLayerWithSquaredError());
}
} else {
layers.add(new FuntionalLayer(new SigmoidFunction()));
}
}
return new FeedForwardTopology(layers);
}
回顾下概念:前馈神经网络被称作网络 (network) 是因为它们通常用许多不同函数复合在一起来表示。该模型与一个有向无环图相关联,图描述了函数是如何复合在一起的。
各神经元从输入层开始,接收前一级输入,并输出到下一级,直至输出层。整个网络中无反馈。其中每一层包含若干个神经元,同一层的神经元之间没有互相连接,层间信息的传送只沿一个方向进行。其中第一层称为输入层。最后一层为输出层.中间为隐含层,简称隐层。隐层可以是一层。也可以是多层。
FeedForwardTopology 是前馈神经网络的拓扑结构,即上述网络层的逻辑展示。这个拓扑里面包含了从隐藏层到输出层的若干层。
/**
* The topology of a feed forward neural network.
*/
public class FeedForwardTopology extends Topology {
/**
* All layers of the topology.
*/
private List<Layer> layers;
}
构建出的拓扑变量大致如下,分为四个层:
- 仿射层
AffineLayer。仿射变换 = 线性变换 + 平移,即h = WX + b; - 功能层
FuntionalLayer,其函数为SigmoidFunction,其为前一个仿射层对应的激活层; - 仿射层
AffineLayer; - 输出层
SoftmaxLayerWithCrossEntropyLoss;
这里仿射层和功能层一起构成了隐藏单元。大多数的隐藏单元可以描述为接受输入向量x,计算仿射变换 z = wTx+b,然后使用一个逐元素的非线性函数g(z)。大多数隐藏单元的区别仅仅在于激活函数 g(z) 的形式。
现在把程序运行时具体变量打印出来让大家更有清晰认识。可以看出来,根据示例代码设定的神经网络参数 .setLayers(new int[]{4, 5, 3}) ,这里的各个层也做了相应设置 : 4,5,3。
this = {
FeedForwardTopology@4951}
layers = {
ArrayList@4944} size = 4
0 = {
AffineLayer@4947} // 仿射层
numIn = 4
numOut = 5
1 = {
FuntionalLayer@4948}
activationFunction = {
SigmoidFunction@4953} // 激活函数
2 = {
AffineLayer@4949} // 仿射层
numIn = 5
numOut = 3
3 = {
SoftmaxLayerWithCrossEntropyLoss@4950} // 激活函数
3.4.1 AffineLayer
是 y=A*x+b 的表示,即仿射层的各种配置信息,Layer properties of affine transformations。
public class AffineLayer extends Layer {
public int numIn;
public int numOut;
public AffineLayer(int numIn, int numOut) {
this.numIn = numIn;
this.numOut = numOut;
}
@Override
public LayerModel createModel() {
return new AffineLayerModel(this);
}
...
}
3.4.2 FuntionalLayer
是 y = f(x) 的表示。这里的 activationFunction 就是 f(x)
public class FuntionalLayer extends Layer {
public ActivationFunction activationFunction;
@Override
public LayerModel createModel() {
return new FuntionalLayerModel(this);
}
}
3.4.3 SoftmaxLayerWithCrossEntropyLoss
3.4.3.1 Softmax
输出函数基本都使用Softmax 函数,其定义如下:
σ i ( Z ) = e x p ( Z i ) ∑ j = 1 m e x p ( z j ) , i = 1 , . . . , m σ_i(Z) = \frac{exp(Z_i)}{\sum_{j=1}^m exp(z_j)}, i = 1,...,m σi(Z)=∑j=1mexp(zj)exp(Zi),i=1,...,m
softmax的输出向量就是概率,是该样本属于各个类的概率!它在 Logistic Regression 里其到的作用是讲线性预测值转化为类别概率。
假设 z_i = W_i + b_i 是第 i 个类别的线性预测结果,带入 Softmax 的结果其实就是先对每一个z_i 取 exponential 变成非负,然后除以所有项之和进行归一化,现在每个 σ_i = σ_i(z) 就可以解释成观察到的数据 x 属于类别 i 的概率,或者称作似然 (Likelihood)。
因此我们训练全连接层的W的目标就是使得其输出的 W.X 在经过 softmax 层计算后其对应于真实标签的预测概率要最高。
3.4.3.2 softmax loss
弄懂了softmax,就要来说说softmax loss了。那softmax loss是什么意思呢??具体如下:
L = − ∑ j = 1 T y j l o g S j L = - \sum_{j=1}^T y_j logS_j L=−j=1∑TyjlogSj
- L是损失。
- Sj是softmax的输出向量S的第j个值,表示的是这个样本属于第j个类别的概率。
- yj前面有个求和符号,j的范围也是1到类别数T,因此 y 是一个1*T的向量,里面的T个值只有1个值是1,其他T-1个值都是0。那么哪个位置的值是1呢?答案是真实标签对应的位置的那个值是1,其他都是0。
所以这个公式其实有一个更简单的形式:
L = − l o g S j L = -logS_j L=−logSj
当然此时要限定 j 是指向当前样本的真实标签。
3.4.3.3 cross entropy
理清了softmax loss,就可以来看看cross entropy了。corss entropy是交叉熵的意思,它的公式如下:
E = − ∑ j = 1 T y j l o g P j E = - \sum_{j=1}^T y_j logP_j E=−j=1∑TyjlogPj
大多数现代的神经网络使用最大似然来训练。这意味着代价函数就是负的对数似然,它与训练数据和模型分布间的交叉熵等价。代价函数的具体形式随着模型而改变。
在信息论中,交叉熵是表示两个概率分布p,q,其中p表示真实分布,q表示非真实分布,在相同的一组事件中,其中用非真实分布q来表示某个事件发生所需要的平均比特数。交叉熵可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。
是不是觉得和softmax loss的公式很像。当cross entropy的输入P是softmax的输出时,cross entropy等于softmax loss。Pj是输入的概率向量P的第j个值,所以如果你的概率是通过softmax公式得到的,那么cross entropy就是softmax loss
使用最大似然来导出代价函数的方法的一个优势是,它减轻了为每个模型设计代价函数的负担。明确一个模型p(y|x)则自动地确定了一个代价函数logp(y|x)。代价函数的梯度必须足够的大和具有足够的预测性,来为学习算法提供一个好的指引。
3.4.3.4 SoftmaxLayerWithCrossEntropyLoss
SoftmaxLayerWithCrossEntropyLoss 是 a softmax layer with cross entropy loss,即带交叉熵损失的softmax层。
public class SoftmaxLayerWithCrossEntropyLoss extends Layer {
@Override
public LayerModel createModel() {
return new SoftmaxLayerModelWithCrossEntropyLoss();
}
}
3.5 构建训练器
回忆示例代码
.setLayers(new int[]{
4, 5, 3})
这里指定了神经网络的结构。输入层是 4个,隐藏层是 5,输出层是 3。
生成训练器的代码如下:
FeedForwardTrainer trainer = new FeedForwardTrainer(topology,
layerSize[0], layerSize[layerSize.length - 1], true, blockSize,
initialWeights);
FeedForwardTrainer 是前馈神经网络的训练器。
public class FeedForwardTrainer implements Serializable {
private Topology topology;
private int inputSize;
private int outputSize;
private int blockSize; // 数据分块大小,默认值64,在压缩时候被stack函数调用到
private boolean onehotLabel;
private DenseVector initialWeights;
}
变量打印如下
trainer = {
FeedForwardTrainer@6456}
topology = {
FeedForwardTopology@6455}
layers = {
ArrayList@4963} size = 4
0 = {
AffineLayer@6461}
1 = {
FuntionalLayer@6462}
2 = {
AffineLayer@6463}
3 = {
SoftmaxLayerWithCrossEntropyLoss@6464}
inputSize = 4
outputSize = 3
blockSize = 64
onehotLabel = true
initialWeights = null
我们可以看到,训练的核心变量是 FeedForwardTrainer,其包含了拓扑模型topology,而topology包含了四层layers。
我们提前把训练器使用的优化器和目标函数也一起展示出来。训练器使用优化器来优化目标函数。
这里优化器是Lbfgs,其包含的目标函数是 AnnObjFunc,包含拓扑和拓扑模型。
public class AnnObjFunc extends OptimObjFunc {
private Topology topology;
private transient TopologyModel topologyModel = null;
}
拓扑模型是依据拓扑生成的,这里是 FeedForwardModel,其中各层对应的模型是AffineLayerModel,FuntionalLayerModel等。
各层模型的作用就是计算损失,梯度等,比如 AffineLayerModel.eval 就是简单的仿射变换 WX + b。
至此,多层感知机第一部分完成。敬请期待后文。
0xFF 参考
深度学习中的深度前馈网络简介
Deep Learning 中文翻译
https://github.com/fengbingchun/NN_Test
深度学习入门——Affine层(仿射层-矩阵乘积)
机器学习——多层感知机MLP的相关公式
多层感知器速成
神经网络(多层感知器)信用卡欺诈检测(一)
手撸ANN之——损失层
【机器学习】人工神经网络ANN
人工神经网络(ANN)的公式推导
[深度学习] [梯度下降]用代码一步步理解梯度下降和神经网络(ANN))
softmax和softmax loss详细解析
Softmax损失函数及梯度的计算
Softmax vs. Softmax-Loss: Numerical Stability
【技术综述】一文道尽softmax loss及其变种
前馈神经网络入门:为什么它很重要?
深度学习基础理解:以前馈神经网络为例
监督学习与回归模型
机器学习——前馈神经网络
AI产品:BP前馈神经网络与梯度问题
深度学习之前馈神经网络(前向传播和误差反向传播)
一文搞懂反向传播算法
★★★★★★关于生活和技术的思考★★★★★★
微信公众账号:罗西的思考
如果您想及时得到个人撰写文章的消息推送,或者想看看个人推荐的技术资料,可以扫描下面二维码(或者长按识别二维码)关注个人公众号)。
![]()