- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
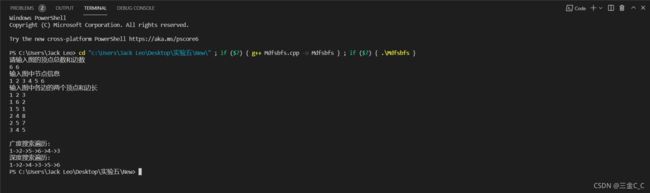
- c++ 的iostream 和 c++的stdio的区别和联系
黄卷青灯77
c++算法开发语言iostreamstdio
在C++中,iostream和C语言的stdio.h都是用于处理输入输出的库,但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系:区别1.编程风格iostream(C++风格):C++标准库中的输入输出流类库,支持面向对象的输入输出操作。典型用法是cin(输入)和cout(输出),使用>操作符来处理数据。更加类型安全,支持用户自定义类型的输入输出。#includeintmain(){in
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- 数组去重
好奇的猫猫猫
整理自js中基础数据结构数组去重问题思考?如何去除数组中重复的项例如数组:[1,3,4,3,5]我们在做去重的时候,一开始想到的肯定是,逐个比较,外面一层循环,内层后一个与前一个一比较,如果是久不将当前这一项放进新的数组,挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低,代码量还多,思考?有没有更好的方法这时候不禁一想当然有了!!!hashtable啊,通过对象的hash办法
- 121. 买卖股票的最佳时机
薄荷糖的味道_fb40
给定一个数组,它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天(股票价格=1)的时候买入,在第5天(股票价格=6)的时候卖出,最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
- 【JS】执行时长(100分) |思路参考+代码解析(C++)
l939035548
JS算法数据结构c++
题目为了充分发挥GPU算力,需要尽可能多的将任务交给GPU执行,现在有一个任务数组,数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务,一次执行耗时1秒,在保证GPU不空闲情况下,最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数,取值范围[1,10000]第二个参数为任务数组长度,取值范围[1,10000]第三个参数为任务数组,数字范围
- 每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
- 回溯算法-重新安排行程
chirou_
算法数据结构图论c++图搜索
leetcode332.重新安排行程这题我还没自己ac过,只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多,用什么数据结构去存数据,去读取数据,都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
- Redis系列:Geo 类型赋能亿级地图位置计算
Ly768768
redisbootstrap数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构,它是基于不同业务场景而设计的:动态字符串(REDIS_STRING):整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
- 基于CODESYS的多轴运动控制程序框架:逻辑与运动控制分离,快速开发灵活操作
GPJnCrbBdl
python开发语言
基于codesys开发的多轴运动控制程序框架,将逻辑与运动控制分离,将单轴控制封装成功能块,对该功能块的操作包含了所有的单轴控制(归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等)。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式,程序状态的跳转都已完成,只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义,能帮助开发者快速
- C++ | Leetcode C++题解之第409题最长回文串
Ddddddd_158
经验分享C++Leetcode题解
题目:题解:classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
- C++菜鸟教程 - 从入门到精通 第二节
DreamByte
c++
一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
- Faiss:高效相似性搜索与聚类的利器
网络·魚
大数据faiss
Faiss是一个针对大规模向量集合的相似性搜索库,由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构,用于加速向量之间的相似性搜索,特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理:近似最近邻搜索:Faiss的核心功能之一是近似最近邻搜索,它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的,
- 数据结构之哈希表
X同学的开始
数据结构数据结构散列表
哈希表(散列表)出现的原因在顺序表中查找时,需要从表头开始,依次遍历比较a[i]与key的值是否相等,直到相等才返回索引i;在有序表中查找时,我们经常使用的是二分查找,通过比较key与a[i]的大小来折半查找,直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是,这两种方法的效率都依赖于查找中比较的次数。我们有一种想法,能不能不经过比较,而是直接通过关键字key一次得到所要的结果呢?这时,
- insert into select 主键自增_mybatis拦截器实现主键自动生成
weixin_39521651
insertintoselect主键自增mybatisdelete返回值mybatisinsert返回主键mybatisinsert返回对象mybatisplusinsert返回主键mybatisplus插入生成id
前言前阵子和朋友聊天,他说他们项目有个需求,要实现主键自动生成,不想每次新增的时候,都手动设置主键。于是我就问他,那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成,因此为了项目稳定性,不会切换id的生成方式。朋友问我有没有什么实现思路,他们公司的orm框架是mybatis,我就建议他说,不然让你老大把mybatis切换成mybatis-plus。mybat
- k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题)
寻找你83497
k均值聚类算法考试例题
?算法:第一步:选K个初始聚类中心,z1(1),z2(1),…,zK(1),其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定,例如可选开始的K个.k均值聚类:---------一种硬聚类算法,隶属度只有两个取值0或1,提出的基本根据是“类内误差平方和最小化”准则;模糊的c均值聚类算法:--------一种模糊聚类算法,是.K均值聚类算法是先随机选取K个对象作为初始的聚类
- Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- 推荐算法_隐语义-梯度下降
_feivirus_
算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵,值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
- K近邻算法_分类鸢尾花数据集
_feivirus_
算法机器学习和数学分类机器学习K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
- Java面试题精选:消息队列(二)
芒果不是芒
Java面试题精选javakafka
一、Kafka的特性1.消息持久化:消息存储在磁盘,所以消息不会丢失2.高吞吐量:可以轻松实现单机百万级别的并发3.扩展性:扩展性强,还是动态扩展4.多客户端支持:支持多种语言(Java、C、C++、GO、)5.KafkaStreams(一个天生的流处理):在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制:Kafka进行生产或者消费的时候会
- 数据结构 | 栈和队列
TT-Kun
数据结构与算法数据结构栈队列C语言
文章目录栈和队列1.栈:后进先出(LIFO)的数据结构1.1概念与结构1.2栈的实现2.队列:先进先出(FIFO)的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中,栈和队列是两种基本且重要的数据结构,它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
- [Python] 数据结构 详解及代码
AIAdvocate
算法python数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
- 4.C_数据结构_队列
荣世蓥
数据结构数据结构
概述什么是队列:队列是限定在两端进行插入操作和删除操作的线性表。具有先入先出(FIFO)的特点相关名词:队尾:写入数据的一段队头:读取数据的一段空队:队列中没有数据,队头指针=队尾指针满队:队列中存满了数据,队尾指针+1=队头指针循环队列1、基本内容循环队列是以数组形式构成的队列数据结构。循环队列的结构体如下:typedefintdata_t;//队列数据类型#defineN64//队列容量typ
- Python算法L5:贪心算法
小熊同学哦
Python算法算法python贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点:缺点:结语贪心算法(GreedyAlgorithm)是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是,在保证每一步局部最优的情况下,希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
- C++ lambda闭包消除类成员变量
barbyQAQ
c++c++java算法
原文链接:https://blog.csdn.net/qq_51470638/article/details/142151502一、背景在面向对象编程时,常常要添加类成员变量。然而类成员一旦多了之后,也会带来干扰。拿到一个类,一看成员变量好几十个,就问你怕不怕?二、解决思路可以借助函数式编程思想,来消除一些不必要的类成员变量。三、实例举个例子:classClassA{public:...intfu
- 2021 CCF 非专业级别软件能力认证第一轮(CSP-J1)入门级C++语言试题 (第三大题:完善程序 代码)
mmz1207
c++csp
最近有一段时间没更新了,在准备CSP考试,请大家见谅。(1)有n个人围成一个圈,依次标号0到n-1。从0号开始,依次0,1,0,1...交替报数,报到一的人离开,直至圈中剩最后一个人。求最后剩下的人的编号。#includeusingnamespacestd;intf[1000010];intmain(){intn;cin>>n;inti=0,cnt=0,p=0;while(cnt#includeu
- 《 C++ 修炼全景指南:九 》打破编程瓶颈!掌握二叉搜索树的高效实现与技巧
Lenyiin
C++修炼全景指南技术指南c++算法stl
摘要本文详细探讨了二叉搜索树(BinarySearchTree,BST)的核心概念和技术细节,包括插入、查找、删除、遍历等基本操作,并结合实际代码演示了如何实现这些功能。文章深入分析了二叉搜索树的性能优势及其时间复杂度,同时介绍了前驱、后继的查找方法等高级功能。通过自定义实现的二叉搜索树类,读者能够掌握其实际应用,此外,文章还建议进一步扩展为平衡树(如AVL树、红黑树)以优化极端情况下的性能退化。
- 20个新手学习c++必会的程序 输出*三角形、杨辉三角等(附代码)
X_StarX
c++学习算法大学生开发语言数据结构
示例1:HelloWorld#includeusingnamespacestd;intmain(){coutusingnamespacestd;intmain(){inta=5;intb=10;intsum=a+b;coutusingnamespacestd;intfactorial(intn){if(nusingnamespacestd;voidprintFibonacci(intn){intt
- java短路运算符和逻辑运算符的区别
3213213333332132
java基础
/*
* 逻辑运算符——不论是什么条件都要执行左右两边代码
* 短路运算符——我认为在底层就是利用物理电路的“并联”和“串联”实现的
* 原理很简单,并联电路代表短路或(||),串联电路代表短路与(&&)。
*
* 并联电路两个开关只要有一个开关闭合,电路就会通。
* 类似于短路或(||),只要有其中一个为true(开关闭合)是
- Java异常那些不得不说的事
白糖_
javaexception
一、在finally块中做数据回收操作
比如数据库连接都是很宝贵的,所以最好在finally中关闭连接。
JDBCAgent jdbc = new JDBCAgent();
try{
jdbc.excute("select * from ctp_log");
}catch(SQLException e){
...
}finally{
jdbc.close();
- utf-8与utf-8(无BOM)的区别
dcj3sjt126com
PHP
BOM——Byte Order Mark,就是字节序标记 在UCS 编码中有一个叫做"ZERO WIDTH NO-BREAK SPACE"的字符,它的编码是FEFF。而FFFE在UCS中是不存在的字符,所以不应该出现在实际传输中。UCS规范建议我们在传输字节流前,先传输 字符"ZERO WIDTH NO-BREAK SPACE"。这样如
- JAVA Annotation之定义篇
周凡杨
java注解annotation入门注释
Annotation: 译为注释或注解
An annotation, in the Java computer programming language, is a form of syntactic metadata that can be added to Java source code. Classes, methods, variables, pa
- tomcat的多域名、虚拟主机配置
g21121
tomcat
众所周知apache可以配置多域名和虚拟主机,而且配置起来比较简单,但是项目用到的是tomcat,配来配去总是不成功。查了些资料才总算可以,下面就跟大家分享下经验。
很多朋友搜索的内容基本是告诉我们这么配置:
在Engine标签下增面积Host标签,如下:
<Host name="www.site1.com" appBase="webapps"
- Linux SSH 错误解析(Capistrano 的cap 访问错误 Permission )
510888780
linuxcapistrano
1.ssh -v
[email protected] 出现
Permission denied (publickey,gssapi-keyex,gssapi-with-mic,password).
错误
运行状况如下:
OpenSSH_5.3p1, OpenSSL 1.0.1e-fips 11 Feb 2013
debug1: Reading configuratio
- log4j的用法
Harry642
javalog4j
一、前言: log4j 是一个开放源码项目,是广泛使用的以Java编写的日志记录包。由于log4j出色的表现, 当时在log4j完成时,log4j开发组织曾建议sun在jdk1.4中用log4j取代jdk1.4 的日志工具类,但当时jdk1.4已接近完成,所以sun拒绝使用log4j,当在java开发中
- mysql、sqlserver、oracle分页,java分页统一接口实现
aijuans
oraclejave
定义:pageStart 起始页,pageEnd 终止页,pageSize页面容量
oracle分页:
select * from ( select mytable.*,rownum num from (实际传的SQL) where rownum<=pageEnd) where num>=pageStart
sqlServer分页:
- Hessian 简单例子
antlove
javaWebservicehessian
hello.hessian.MyCar.java
package hessian.pojo;
import java.io.Serializable;
public class MyCar implements Serializable {
private static final long serialVersionUID = 473690540190845543
- 数据库对象的同义词和序列
百合不是茶
sql序列同义词ORACLE权限
回顾简单的数据库权限等命令;
解锁用户和锁定用户
alter user scott account lock/unlock;
//system下查看系统中的用户
select * dba_users;
//创建用户名和密码
create user wj identified by wj;
identified by
//授予连接权和建表权
grant connect to
- 使用Powermock和mockito测试静态方法
bijian1013
持续集成单元测试mockitoPowermock
实例:
package com.bijian.study;
import static org.junit.Assert.assertEquals;
import java.io.IOException;
import org.junit.Before;
import org.junit.Test;
import or
- 精通Oracle10编程SQL(6)访问ORACLE
bijian1013
oracle数据库plsql
/*
*访问ORACLE
*/
--检索单行数据
--使用标量变量接收数据
DECLARE
v_ename emp.ename%TYPE;
v_sal emp.sal%TYPE;
BEGIN
select ename,sal into v_ename,v_sal
from emp where empno=&no;
dbms_output.pu
- 【Nginx四】Nginx作为HTTP负载均衡服务器
bit1129
nginx
Nginx的另一个常用的功能是作为负载均衡服务器。一个典型的web应用系统,通过负载均衡服务器,可以使得应用有多台后端服务器来响应客户端的请求。一个应用配置多台后端服务器,可以带来很多好处:
负载均衡的好处
增加可用资源
增加吞吐量
加快响应速度,降低延时
出错的重试验机制
Nginx主要支持三种均衡算法:
round-robin
l
- jquery-validation备忘
白糖_
jquerycssF#Firebug
留点学习jquery validation总结的代码:
function checkForm(){
validator = $("#commentForm").validate({// #formId为需要进行验证的表单ID
errorElement :"span",// 使用"div"标签标记错误, 默认:&
- solr限制admin界面访问(端口限制和http授权限制)
ronin47
限定Ip访问
solr的管理界面可以帮助我们做很多事情,但是把solr程序放到公网之后就要限制对admin的访问了。
可以通过tomcat的http基本授权来做限制,也可以通过iptables防火墙来限制。
我们先看如何通过tomcat配置http授权限制。
第一步: 在tomcat的conf/tomcat-users.xml文件中添加管理用户,比如:
<userusername="ad
- 多线程-用JAVA写一个多线程程序,写四个线程,其中二个对一个变量加1,另外二个对一个变量减1
bylijinnan
java多线程
public class IncDecThread {
private int j=10;
/*
* 题目:用JAVA写一个多线程程序,写四个线程,其中二个对一个变量加1,另外二个对一个变量减1
* 两个问题:
* 1、线程同步--synchronized
* 2、线程之间如何共享同一个j变量--内部类
*/
public static
- 买房历程
cfyme
2015-06-21: 万科未来城,看房子
2015-06-26: 办理贷款手续,贷款73万,贷款利率5.65=5.3675
2015-06-27: 房子首付,签完合同
2015-06-28,央行宣布降息 0.25,就2天的时间差啊,没赶上。
首付,老婆找他的小姐妹接了5万,另外几个朋友借了1-
- [军事与科技]制造大型太空战舰的前奏
comsci
制造
天气热了........空调和电扇要准备好..........
最近,世界形势日趋复杂化,战争的阴影开始覆盖全世界..........
所以,我们不得不关
- dateformat
dai_lm
DateFormat
"Symbol Meaning Presentation Ex."
"------ ------- ------------ ----"
"G era designator (Text) AD"
"y year
- Hadoop如何实现关联计算
datamachine
mapreducehadoop关联计算
选择Hadoop,低成本和高扩展性是主要原因,但但它的开发效率实在无法让人满意。
以关联计算为例。
假设:HDFS上有2个文件,分别是客户信息和订单信息,customerID是它们之间的关联字段。如何进行关联计算,以便将客户名称添加到订单列表中?
&nbs
- 用户模型中修改用户信息时,密码是如何处理的
dcj3sjt126com
yii
当我添加或修改用户记录的时候对于处理确认密码我遇到了一些麻烦,所有我想分享一下我是怎么处理的。
场景是使用的基本的那些(系统自带),你需要有一个数据表(user)并且表中有一个密码字段(password),它使用 sha1、md5或其他加密方式加密用户密码。
面是它的工作流程: 当创建用户的时候密码需要加密并且保存,但当修改用户记录时如果使用同样的场景我们最终就会把用户加密过的密码再次加密,这
- 中文 iOS/Mac 开发博客列表
dcj3sjt126com
Blog
本博客列表会不断更新维护,如果有推荐的博客,请到此处提交博客信息。
本博客列表涉及的文章内容支持 定制化Google搜索,特别感谢 JeOam 提供并帮助更新。
本博客列表也提供同步更新的OPML文件(下载OPML文件),可供导入到例如feedly等第三方定阅工具中,特别感谢 lcepy 提供自动转换脚本。这里有导入教程。
- js去除空格,去除左右两端的空格
蕃薯耀
去除左右两端的空格js去掉所有空格js去除空格
js去除空格,去除左右两端的空格
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>&g
- SpringMVC4零配置--web.xml
hanqunfeng
springmvc4
servlet3.0+规范后,允许servlet,filter,listener不必声明在web.xml中,而是以硬编码的方式存在,实现容器的零配置。
ServletContainerInitializer:启动容器时负责加载相关配置
package javax.servlet;
import java.util.Set;
public interface ServletContainer
- 《开源框架那些事儿21》:巧借力与借巧力
j2eetop
框架UI
同样做前端UI,为什么有人花了一点力气,就可以做好?而有的人费尽全力,仍然错误百出?我们可以先看看几个故事。
故事1:巧借力,乌鸦也可以吃核桃
有一个盛产核桃的村子,每年秋末冬初,成群的乌鸦总会来到这里,到果园里捡拾那些被果农们遗落的核桃。
核桃仁虽然美味,但是外壳那么坚硬,乌鸦怎么才能吃到呢?原来乌鸦先把核桃叼起,然后飞到高高的树枝上,再将核桃摔下去,核桃落到坚硬的地面上,被撞破了,于是,
- JQuery EasyUI 验证扩展
可怜的猫
jqueryeasyui验证
最近项目中用到了前端框架-- EasyUI,在做校验的时候会涉及到很多需要自定义的内容,现把常用的验证方式总结出来,留待后用。
以下内容只需要在公用js中添加即可。
使用类似于如下:
<input class="easyui-textbox" name="mobile" id="mobile&
- 架构师之httpurlconnection----------读取和发送(流读取效率通用类)
nannan408
1.前言.
如题.
2.代码.
/*
* Copyright (c) 2015, S.F. Express Inc. All rights reserved.
*/
package com.test.test.test.send;
import java.io.IOException;
import java.io.InputStream
- Jquery性能优化
r361251
JavaScriptjquery
一、注意定义jQuery变量的时候添加var关键字
这个不仅仅是jQuery,所有javascript开发过程中,都需要注意,请一定不要定义成如下:
$loading = $('#loading'); //这个是全局定义,不知道哪里位置倒霉引用了相同的变量名,就会郁闷至死的
二、请使用一个var来定义变量
如果你使用多个变量的话,请如下方式定义:
. 代码如下:
var page
- 在eclipse项目中使用maven管理依赖
tjj006
eclipsemaven
概览:
如何导入maven项目至eclipse中
建立自有Maven Java类库服务器
建立符合maven代码库标准的自定义类库
Maven在管理Java类库方面有巨大的优势,像白衣所说就是非常“环保”。
我们平时用IDE开发都是把所需要的类库一股脑的全丢到项目目录下,然后全部添加到ide的构建路径中,如果用了SVN/CVS,这样会很容易就 把
- 中国天气网省市级联页面
x125858805
级联
1、页面及级联js
<%@ page language="java" import="java.util.*" pageEncoding="UTF-8"%>
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN">
&l