数学建模预测模型实例（三）---双色球概率预测模型
双色球概率预测模型
数学建模预测模型实例（一）—大学生体测数据模型
数学建模预测模型实例（二）—表白墙影响力量化模型
python预测算法—线性回归
双色球概率预测模型
前言
最近新晋彩民佩瑞对于双色球产生了极为浓厚的兴趣，在买过几注随机号码中奖无果后，决心潜心修炼，钻研一个比较靠谱的预测方法！所以有了这篇文章，文章思路及结果仅供娱乐，请勿当真！
建模思路
在产生这个想法之后我首先查阅了网络上各种各样的双色球预测模型，发现了几类具有代表性的：
1.基于神经网络的回归预测模型
2.基于LSTM的预测模型
3.基于深度学习的预测模型
看到这三种预测模型是不是觉得很高深，没错！我也是这样的感觉！所以我又开始了新一轮的资料搜索，这次去详细的了解了一下有关双色球的概率知识。
有关双色球的概率知识
双色球由红球和蓝球两部份组成，红球是由01到33个号码中选择，蓝球是由01到16个号码中选择。每次开奖在红色球中随机摇出六个红号,在蓝球中随机摇出一个蓝号。
这里以一等奖为例，双色球可以简单的理解为一次不放回抽样，因此计算其概率需要用到高中数学的概率计算：
从这里不难看出，1700万分之一的一等奖几率是有多么渺茫；而且双色球作为一个完全随机的过程，我们从中得到的信息是十分有限的，只能从历史数据反映出来的大致概率分布入手去建立模型，而由于各类学习算法的操作对象都是连续变化或者与时间序列高度
相关的数据，双色球并不满足这个条件。
因此我最终没有应用或改进现有的算法去预测结果，反倒是选择了概率，这个唯一看起来不那么玄学的方向。
如果只考虑概率这个方向，那么就不得不与日期产生联系，即在每个特定日期下双色球每一种可能组合的中奖概率是否会不同？由此我们得到了我们的科学问题。
探索性数据分析
至此确定了大方向为概率之后，我立马开始着手观察数据。
此次实验获取到的数据为2003-2020.8月的双色球历史一等奖的中奖数据。
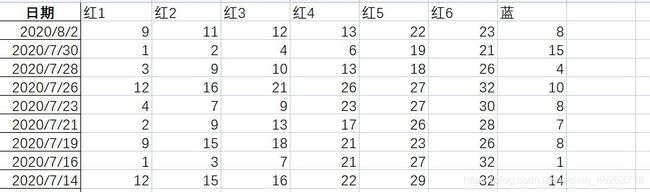
数据预处理
经过观察，我认为这样的数据呈现方式不够直观，因此我选择将七个球的中奖数据分割开，由于每一种球的每一次抽取都有33（红）或16（蓝）种可能，我将每一可能作为一列，以1，0来表示是否中奖，具体如下图(以红色1号球为例)。
def process_df(df_w_1):
'''
通过这一步将每一个球的历史获奖数据按照33（红）/16（蓝）种可能性进行二元归一
'''
ball = np.arange(1,34)
for b in ball:
name = str(b)+'号'
l=[]
for i in range(len(df_w_1)):
if int(df_w_1.iloc[i,1])==b:
l.append(1)
else:
l.append(0)
df_w_1[name]=pd.DataFrame(l)
return df_w_1
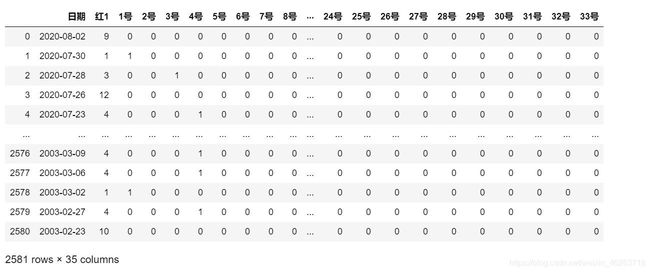
1号-33号这33种可能性在每一个日期下的中奖情况都被表示出来了！
历史趋势可视化
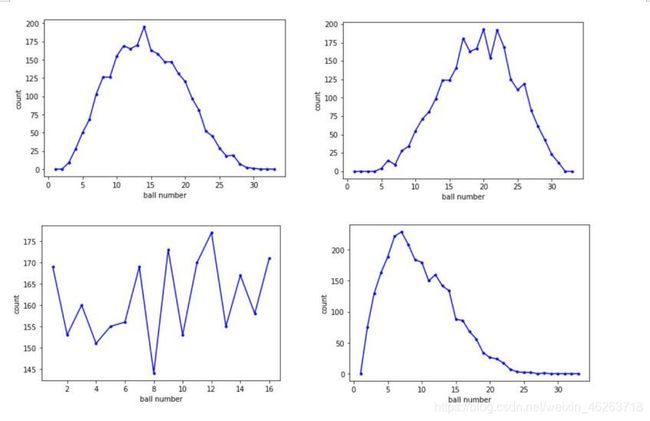
为了得到进一步的建模思路，我选择对历史数据中的每个球的获奖号码进行可视化的分析。结果如下（这里只选取其中四个球的结果进行展示）。
def draw(df_w_1):
'''
数据探索阶段获取7个球33/16种结果的历史获奖趋势
'''
sum_list=[]
ball = np.arange(1,34)
for b in ball:
sum_b = df_w_1.iloc[:,b+1].sum()
sum_list.append(sum_b)
print(sum_list)
plt.plot(ball,sum_list,'b.-')
plt.xlabel('ball number')
plt.ylabel('count')
plt.show()
看到上面的图表之后，我又一次肯定了概率这条路一定能走通!
上图只选取了三个红球和一个蓝球的历史数据趋势作为展示，横坐标为一个球可能的33（红）或16（蓝）种结果，纵坐标为每一种可能结果中奖的计数。上图很好的反映出了在大量历史数据中的确存在一定的中奖趋势，由此可导致每种球每一种可能的中奖概率不同。
到这里我们还是没有一个清晰可行的具体思路，所以我想到我们不应该只关注中奖结果，那些没中奖的结果同样值得注意，除此之外还有日期与它们的关系。
日期与是否获奖可视化
考虑到数据点数量太多可能不利于我们观察，在这里我随机选取了2581条数据中的100条进行接下来的数据探索。
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
sns.set(font='SimHei')
data['month']=data['日期'].dt.month
data['day']=data['日期'].dt.day
data1=data[['day','3号']]
train_,test_ = train_test_split(data1,test_size=100)
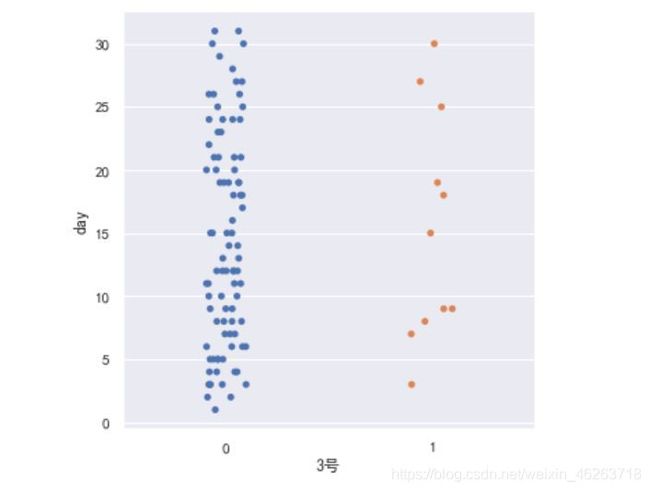
sns.catplot(x='3号',y='day',data=test_)
上图展示的是1号红球的号码3的获奖结果与我们的天数的分布。
这张图是不是看着很像一个聚类数据？没有获奖的结果与天数并没有呈现这样的分群分布，因此观察到这种不寻常现象的我决定深入下去。
既然获奖结果与天数呈现一定程度上的分群，那么如果我们可以利用这种分群把一个月31天划分为几个区间，通过区间内获奖概率进行赋值，再加上每一天的获奖概率，那么一个月31天就被划分为了31个方格，每一个方格都有自己的分值，分值越高则该号数获奖可能性越高，换言之，我们的模型思路出来了！
系统思路
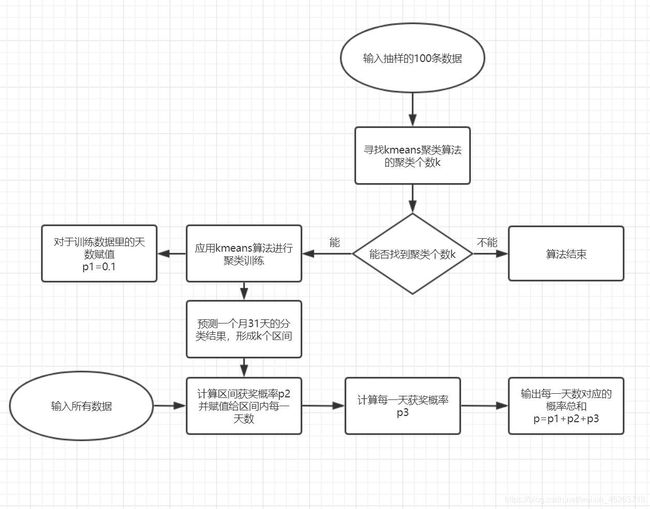
在这里还想解释一下p1，因为我们的训练数据是随机选取的100条数据，所以这里的天数我们暂时通过p1打一个标记（现在姑且认为是幸运数字的奖励吧！）
好了，现在系统思路都出来了！我们就开始代码实现吧！
代码实现
选定聚类个数k
def select_k(x):
'''
聚类时选定最佳聚类个数k
'''
SSE=[]
k_=[]
for k in range(1, 9):
estimator = KMeans(n_clusters=k)
estimator.fit(x)
SSE.append(estimator.inertia_)
for i in range(len(SSE)):
if i+1<len(SSE):
if SSE[i]-SSE[i+1]<=20:
k_.append(i+1)
return k_[0]
按照三个标准进行赋分
def process_data(namef,test_,data):
'''
按照三个标准进行赋分
'''
num_list=[]
everyday_p=[]
day_data = pd.DataFrame(pd.read_excel(r'C:\Users\15643\Desktop\history_data.xlsx',sheet_name='Sheet1'))
for m in range(len(namef)):
try:
na = namef[m]
test_na = test_.loc[test_[na]==1]
x=test_na['day']
x = np.array(x)
x = x.reshape(-1, 1)
k = select_k(x)
####kmeans聚类
kms = KMeans(n_clusters=k)
kms.fit(x)
day_list = np.arange(1,32)
day_list_ = day_list.reshape(-1, 1)
y = kms.predict(day_list_)
####对于训练数据里的天数赋值p1=0.1
day_data_col = namef2[:31]
day_data.columns = day_data_col
for l in range(len(x)):
for j in range(0,31):
if x[l]==j+1:
day_data.iloc[m,j]=1.1
###计算区间获奖概率p2并赋值给区间内每一天数
###计算每一天获奖概率p3
for day in day_list:
c = data.loc[data['day']==int(day)]
num = len(c)
num_list.append(num)
y =pd.DataFrame(y)
y['day']=pd.DataFrame(day_list)
y['num']=pd.DataFrame(num_list)
y.columns=['classify','day','num']
everyday = y['num']
for i in range(k):
l=y.loc[y['classify']==i]
l_num =l['num'].sum(axis=0)
l_f = l_num/y['num'].sum(axis=0)
y['classify']=y['classify'].replace(i,l_f)
cls = y['classify']
for i in range(31):
everyday_p.append(everyday[i]/y['num'].sum(axis=0))
###输出每一天数对应的概率总和p=p1+p2+p3
day_data.iloc[m,i]=day_data.iloc[m,i]+cls[i]+everyday_p[i]
except:
pass
return day_data
调用之前的所有函数
def data(data,data_w1):
'''
调用之前的所有函数
'''
data['month']=data['日期'].dt.month
data['day']=data['日期'].dt.day
data = data.drop(['日期'],axis=1)
name = data.columns
namef=name[1:17]
train_,test_ = train_test_split(data,test_size=100)#在总共2581个数据中随机选取100个数据进行聚类分析
day_f = process_data(namef,test_,data)
return day_f
输出结果
data_w1 = process_df(df_w_1)
data_w2 = process_df(df_w_2)
data_w3 = process_df(df_w_3)
data_w4 = process_df(df_w_4)
data_w5 = process_df(df_w_5)
data_w6 = process_df(df_w_6)
w1=data(data_w1)
w2=data(data_w2)
w3=data(data_w3)
w4=data(data_w4)
w5=data(data_w5)
w6=data(data_w6)
def select_whiteb_ball(day):
'''
根据输入日期输出最佳组合的函数
'''
result=[]
col=int(day)
w1_s = w1.iloc[:,col]
w2_s = w2.iloc[:,col]
w3_s = w3.iloc[:,col]
w4_s = w4.iloc[:,col]
w5_s = w5.iloc[:,col]
w6_s = w6.iloc[:,col]
b_s = b.iloc[:,col]
w1_s=np.array(w1_s)
w2_s=np.array(w2_s)
w3_s=np.array(w3_s)
w4_s=np.array(w4_s)
w5_s=np.array(w5_s)
w6_s=np.array(w6_s)
b_s = np.array(b_s)
w1f=np.argwhere(w1_s == w1_s.max())
w2f=np.argwhere(w2_s == w2_s.max())
w3f=np.argwhere(w3_s == w3_s.max())
w4f=np.argwhere(w4_s == w4_s.max())
w5f=np.argwhere(w5_s == w5_s.max())
w6f=np.argwhere(w6_s == w6_s.max())
bf=np.argwhere(b_s == b_s.max())
result.append([int(w1f)+1,int(w2f)+1,int(w3f)+1,int(w4f)+1,int(w5f)+1,int(w6f)+1,int(bf)+1])
print('推荐您的最佳组合为：{}'.format(result))
最终结果
结果分析
根据最后的结果我发现
p1=0.1
0.1
所以我们对这三个赋分标准进行重要性排序
1.聚类区间中每种球每种可能性获奖概率p2
2.幸运数字加持p2
3.每一天每种球每种可能性获奖概率p3
最后结果选择就是以输入天数下所对应的各球各可能性的得分，得分越高，说明该种可能越有可能获奖。
模型不足
1.对于无法找到聚类个数k的各球各可能性的数据，现阶段还无法进一步分析
碍于本人知识储备不足，实乃大憾！
2.结果可能相对固定，不像应用成熟算法的模型可以有较强的灵活性
3.模型还是不靠谱！仅供娱乐！哈哈哈哈！希望大家玩的开心！
数据及源码获取 提取码：bwlw
最后希望大家看完这篇文章后能多多支持奇趣多多！
你们的关注是对我们最大的鼓励！
