数字图像处理——直方图均衡化与颜色迁移算法的c++实现
项目源代码下载链接(VS2015)
1.直方图均衡化
主要思想:
把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。
直方图均衡化的基本思想是把原始图的直方图变换为均匀分布的形式,这样就增加了象素灰度值的动态范围从而可达到增强图像整体对比度的效果。设原始图像在(x,y)处的灰度为f,而改变后的图像为g,则对图像增强的方法可表述为将在(x,y)处的灰度f映射为g。在灰度直方图均衡化处理中对图像的映射函数可定义为:g = EQ (f),这个映射函数EQ(f)必须满足两个条件(其中L为图像的灰度级数):
(1)EQ(f)在0≤f≤L-1范围内是一个单值单增函数。这是为了保证增强处理没有打乱原始图像的灰度排列次序,原图各灰度级在变换后仍保持从黑到白(或从白到黑)的排列。
(2)对于0≤f≤L-1有0≤g≤L-1,这个条件保证了变换前后灰度值动态范围的一致性。
累积分布函数(cumulative distribution function,CDF)即可以满足上述两个条件,并且通过该函数可以完成将原图像f的分布转换成g的均匀分布。此时的直方图均衡化映射函数为: = EQ( ) = (ni/n) = pf() ,(k=0,1,2,……,L-1)
上述求和区间为0到k,根据该方程可以由源图像的各像素灰度值直接得到直方图均衡化后各像素的灰度值。在实际处理变换时,一般先对原始图像的灰度情况进行统计分析,并计算出原始直方图分布,然后根据计算出的累计直方图分布求出到的灰度映射关系。在重复上述步骤得到源图像所有灰度级到目标图像灰度级的映射关系后,按照这个映射关系对源图像各点像素进行灰度转换,即可完成对源图的直方图均衡化。
c++实现主要代码:
//统计灰度频率直方图
cimg_forXY(image, i, j) {
if (image.spectrum() == 1) greyCount[image(i, j)]++;
else if (image.spectrum() == 3) {
rCount[image(i, j, 0)]++;
gCount[image(i, j, 1)]++;
bCount[image(i, j, 2)]++;
}
//累加,扩展到[0, 255],得到新的灰度级for (i = 1; i < dim; i++) {
greyCount[i] += greyCount[i - 1];
bCount[i] += bCount[i - 1];
gCount[i] += gCount[i - 1];
rCount[i] += rCount[i - 1];
//扩展到[0, 255]
greyNew[i] = ((float)greyCount[i] / image._width / image._height) * (dim - 1) + 0.5;
bNew[i] = ((float)bCount[i] / image._width / image._height) * (dim - 1) + 0.5;
rNew[i] = ((float)rCount[i] / image._width / image._height) * (dim - 1) + 0.5;
gNew[i] = ((float)gCount[i] / image._width / image._height) * (dim - 1) + 0.5;
}
//灰度转换
//如果是灰度图
if (image.spectrum() == 1) {
cimg_forXY(image, i, j) {
image(i, j) = (unsigned char)(greyNew[image(i, j)]);
}
}
//如果是彩色图片
else if (image.spectrum() == 3) {
cimg_forXY(image, i, j) {
image(i, j, 0) = (unsigned char)(rNew[image(i, j, 0)]);
image(i, j, 1) = (unsigned char)(gNew[image(i, j, 1)]);
image(i, j, 2) = (unsigned char)(bNew[image(i, j, 2)]);
}
}
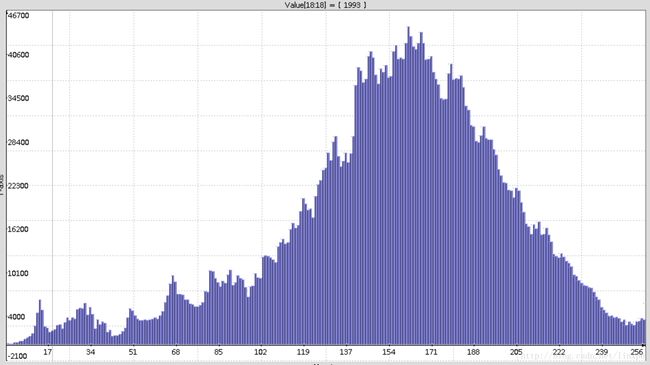
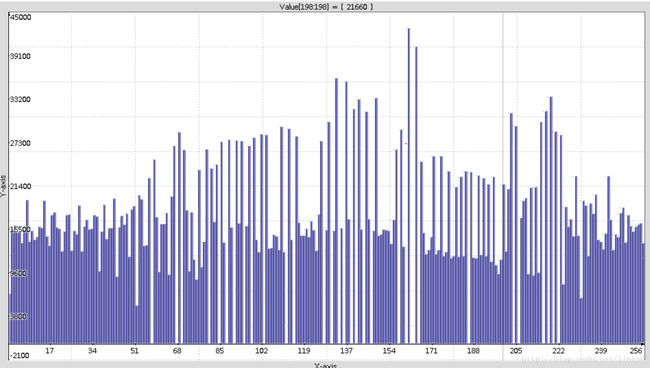
效果展示:
直方图均衡化效果:
2.颜色迁移
Welsh等人在Reinhard等人的彩色图像间色彩迁移算法的基础上,提出了灰度图像彩色化的思想,并提出了相应的算法。该算法主要利用查找匹配像素来实现灰度图像的色彩迁移,因为灰度图像只有亮度信息,所以该算法主要通过像素的亮度值匹配,来实现灰度图像的自动彩色化。
具体步骤如下:
(1)将参考图像和灰度图像分别由RGB空间转换到lαβ色彩空间。
(2)根据灰度图像的亮度及标准差,对参考图像进行亮度重映射。
由于参考图像和灰度图像的直方图取值不一定在同一范围,那么如果将一幅亮度值很低的参考图像与一幅亮度值很高的目标图像的直方图进行对比将会出现较大的误差。因此,需要对参考图像进行亮度重映射:
L = (nl’ / nl)* (l – ml) + ml’
其中,l是源图像l通道的数据,L是变换后得到新的源图像l通道的值,ml和ml’ 分别是源图像和着色图像的l通道的均值,nl和nl’表示它们的l通道标准方差。
(3)从参考图像中随机选取一批样本点,将像素点的亮度和邻域范围内亮度的标准差的线性组合值作为权值,计算公式如下:
W = l/2 + σ/2
其中,w为权值,l为像素点的亮度值,σ为该像素点周围某个邻域内亮度值的标准差。关于邻域的大小,Welsh指出一般取5X5,对个别图像取更大的邻域效果会更好。
(4)按行扫描灰度图像,对于每个像素点,由公式计算其权值,并在参考图像的样本点中找到一个最接近的样本点,即最佳匹配点,将匹配点的仅和口通道的值赋给灰度图像的对应像素点,从而实现色彩的传递。
(5)将参考图像和灰度图像从lαβ空间转换到RGB空间。
c++实现:
void Color_Transfer::ConvertToLab(CImg
double temp[3];
memset(temp, 0, sizeof(double) * 3);
cimg_forXY(img, x, y) {
temp[0] = 0.3811 * img(x, y, 0, 0) + 0.5783 * img(x, y, 0, 1) + 0.0402 * img(x, y, 0, 2);
temp[1] = 0.1967 * img(x, y, 0, 0) + 0.7244 * img(x, y, 0, 1) + 0.0782 * img(x, y, 0, 2);
temp[2] = 0.0241 * img(x, y, 0, 0) + 0.1288 * img(x, y, 0, 1) + 0.8444 * img(x, y, 0, 2);
for (int i = 0;i < 3;++i) temp[i] = temp[i] == 0 ? 1 : log(temp[i]);
img(x, y, 0, 0) = (temp[0] + temp[1] + temp[2]) / sqrt(3.0);
img(x, y, 0, 1) = (temp[0] + temp[1] - 2 * temp[2]) / sqrt(6.0);
img(x, y, 0, 2) = (temp[0] - temp[1]) / sqrt(2.0);
}
}
void Color_Transfer::Process() {
double srcMean[3], srcDeviation[3], tarMean[3], tarDeviation[3];
for (int i = 0; i < 3; i++) { srcMean[i] = 0; srcDeviation[i] = 0; tarMean[i] = 0; tarDeviation[i] = 0; }
cimg_forXY(target, x, y) {
for (int i = 0; i < 3; i++) {
tarMean[i] += (target(x, y, 0, i) / (target._width * target._height));
}
}
//mean
cimg_forXY(source, x, y) {
for (int i = 0; i < 3; i++)
srcMean[i] += (source(x, y, 0, i) / (source._width * source._height));
}
//deviation
cimg_forXY(source, x, y) {
for (int i = 0; i < 3; i++)
srcDeviation[i] += (source(x, y, 0, i) - srcMean[i]) * (source(x, y, 0, i) - srcMean[i]);
}
for (int i = 0; i < 3; i++) srcDeviation[i] = sqrt(srcDeviation[i] / source._width /source._height);
cimg_forXY(target, x, y) {
for (int i = 0; i < 3; i++)
tarDeviation[i] += (target(x, y, 0, i) - tarMean[i]) * (target(x, y, 0, i) - tarMean[i]);
}
for (int i = 0; i < 3; i++) tarDeviation[i] = sqrt(tarDeviation[i] / target._width / target._height);
cimg_forXY(source, x, y) {
for (int i = 0; i < 3; i++)
source(x, y, 0, i) = (source(x, y, 0, i) - srcMean[i]) * tarDeviation[i] / srcDeviation[i];
}
cimg_forXY(source, x, y) {
for (int i = 0; i < 3; i++)
source(x, y, 0, i) += tarMean[i];
}
}
void Color_Transfer::ConvertBackToRGB() {double temp[3];
memset(temp, 0, sizeof(double) * 3);
int rMax = source(0, 0, 0, 0), gMax = source(0, 0, 0, 0);
int bMax = source(0, 0, 0, 1), rMin = source(0, 0, 0, 1);
int gMin = source(0, 0, 0, 2), bMin = source(0, 0, 0, 2);
cimg_forXY(source, x, y) {
temp[0] = exp(source(x, y, 0, 0) * sqrt(3) / 3 + source(x, y, 0, 1) * sqrt(6) / 6 + source(x, y, 0, 2) * sqrt(2) / 2);
temp[1] = exp(source(x, y, 0, 0) * sqrt(3) / 3 + source(x, y, 0, 1) * sqrt(6) / 6 - source(x, y, 0, 2) * sqrt(2) / 2);
temp[2] = exp(source(x, y, 0, 0) * sqrt(3) / 3 - source(x, y, 0, 1) * sqrt(6) / 3);
source(x, y, 0, 0) = 4.4679 * temp[0] + 3.5873 * temp[1] + 0.1193 * temp[2];
rMax = rMax > source(x, y, 0, 0) ? rMax : source(x, y, 0, 0);
rMin = rMin > source(x, y, 0, 0) ? source(x, y, 0, 0) : rMin;
source(x, y, 0, 1) = -1.2186 * temp[0] + 2.3809 * temp[1] + 0.1624 * temp[2];
gMax = gMax > source(x, y, 0, 1) ? gMax : source(x, y, 0, 1);
gMin = gMin > source(x, y, 0, 1) ? source(x, y, 0, 1) : gMin;
source(x, y, 0, 2) = 0.0497 * temp[0] - 0.2439 * temp[1] + 1.2045 * temp[2];
bMax = bMax > source(x, y, 0, 2) ? bMax : source(x, y, 0, 2);
bMin = bMin > source(x, y, 0, 2) ? source(x, y, 0, 2) : bMin;
}
cimg_forXY(result, x, y) {
result(x, y, 0, 0) = (unsigned char)255 * (source(x, y, 0, 0) - rMin) / (rMax - rMin);
result(x, y, 0, 1) = (unsigned char)255 * (source(x, y, 0, 1) - gMin) / (gMax - gMin);
result(x, y, 0, 2) = (unsigned char)255 * (source(x, y, 0, 2) - bMin) / (bMax - bMin);
}
}
效果图: