机器学习sklearn----支持向量机SVC重要参数核函数kernel如何选择
文章目录
-
- 前言
- 不同核函数对比分析
-
- 创建原始数据
- 不同核函数表现可视化
- 总结
前言
前面的SVC求解可视化一文中已经知道了SVC对于线性和非线性的数据有不同的核函数,线性只有一个,而非线性有三个,实际生活中我们遇到的数据大多数是非线性的,那么这些核函数具体应该怎么选择呢?
SVM的核函数:
- linear:线性核函数,只能解决线性问题
- ploy:多项式核函数,解决非线性问题和线性问题,但是偏线性
- sigmoid:双曲正切核函数,解决线性和非线性问题
- rbf:高斯径向基核函数,解决线性和非线性问题,偏非线性
核函数可以理解为将低维数据变换到高维数据,方便找到决策边界的这样一个数学过程
核函数的数学原理很复杂,这里不探究了,主要关注核函数在不同数据集上的选择
本文中使用到的第三方库
from sklearn.svm import SVC
from sklearn.datasets import make_blobs, make_moons, make_circles, make_classification
from sklearn.model_selection import cross_val_score # 交叉验证
import numpy as np
import matplotlib.pyplot as plt
import warnings
%matplotlib inline
warnings.filterwarnings("ignore")
不同核函数对比分析
创建原始数据
# 创建数据集
n_samples = 200
n_features = 2
datas = [
make_blobs(n_samples=n_samples, n_features=n_features, centers=2, cluster_std=8, random_state=1),
make_moons(n_samples=n_samples, noise=0.2, random_state=1),
make_circles(n_samples=n_samples, factor=0.6, noise=0.2, random_state=1),
make_classification(n_samples=n_samples, n_features=n_features, n_informative=2, n_redundant=0, random_state=2)
]
# datas的格式如下:[(X, y), (X, y)]
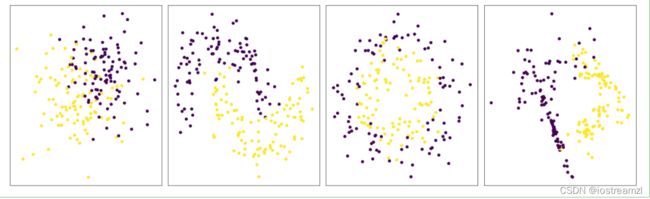
# 展示原始数据集
fig, axes = plt.subplots(1, 4)
fig.set_size_inches(20, 6)
for i in range(len(datas)) :
X, y = datas[i]
ax = axes[i]
ax.set_xticks([])
ax.set_yticks([])
ax.scatter(X[:, 0], X[:, 1], c=y)
plt.tight_layout() # 让图片显示更加的紧密
plt.show()
不同核函数表现可视化
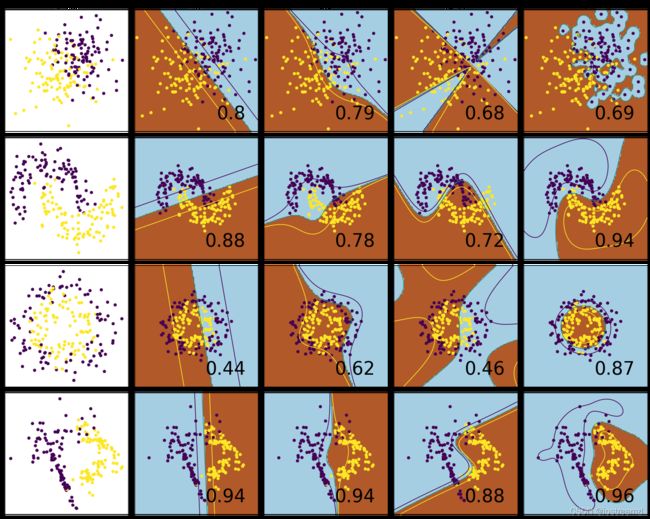
# 画出不同的核函数在不同分布的数据上的表现以及决策边界
# 需要一张5X4的画布,第一列是原始数据,后面依次是每个核函数在数据集上的表现
# 在图的最上方显示核函数类型,在每张图上显示对应核函数的得分
kernels = ['linear', 'poly', 'sigmoid', 'rbf']
fig, charts = plt.subplots(4, 5) # charts.shape=(4, 5)
fig.set_size_inches(20, 16)
for row, line_plots in enumerate(charts) :
# row: 每一个子图的行号
# line_plots: 每一行对应的子图
# 获得特征标签数据集
X, y = datas[row]
row_data_ax = charts[row][0]
row_data_ax.scatter(X[:, 0], X[:, 1], c=y)
# 不显示坐标轴数字
row_data_ax.set_xticks([])
row_data_ax.set_yticks([])
if row == 0 :
row_data_ax.set_title("row data")
for col, ax in enumerate(line_plots[1:]) :
# col:每一行每个子图对应的列索引
# ax:每一行中的每个子图对象
# 获得核函数
kernel = kernels[col]
# 在第一行显示核函数的名称
if row == 0 :
ax.set_title(kernel)
# 不显示坐标轴数字
ax.set_xticks([])
ax.set_yticks([])
# 实例化模型
svc = SVC(kernel=kernel).fit(X, y)
# 交叉验证取均值作为模型得分
score = round(cross_val_score(svc, X, y, cv=5).mean(), 2)
# 画决策边界
xmin, xmax = X[:, 0].min() - 1, X[:, 0].max() + 1
ymin, ymax = X[:, 1].min() - 1, X[:, 1].max() + 1
# 取出大量的网格坐标点,作为特征矩阵
xloc, yloc = np.meshgrid(np.linspace(xmin, xmax, 100),
np.linspace(ymin, ymax, 100))
coo = np.vstack((xloc.ravel(), yloc.ravel())).T
# 计算每个特征点到决策边界的距离,作为等高线的高度
dis = svc.decision_function(coo).reshape(xloc.shape)
# 将等高线途中决策边界两边填充为不同的颜色
ax.pcolormesh(xloc, yloc, dis>0, cmap=plt.cm.Paired)
# 画等高线
ax.contour(xloc, yloc, dis, levels=[-1, 0, 1])
# 在图上显示模型得分, 相对于坐标轴在右下方显示,需要参数transform来定位
ax.text(0.9, 0.1, str(score), horizontalalignment='right', size=40,
transform=ax.transAxes)
# 画原始数据散点图
ax.scatter(X[:, 0], X[:, 1], c=y)
plt.tight_layout()
plt.show()
总结
从上面的结果来看,rbf在几个不同分类的数据集上的表现都比较好,索引日常使用中我们可以优先考虑rbf,然后再使用其他的核函数。一般来说rbf表现不佳,其他的核函数对结果的提升效果也不会很高了