基于支持向量机的分类预测
1.认识SVM
支持向量机(Support Vector Machine, SVM)是一种对数据进行二分类的广义线性分类器,其分类边界是对学习样本求解的最大间隔超平面。
SVM使用铰链损失函数计算经验风险并在求解系统中加入了正则化项以优化结构风险,是一个具有稀疏性和稳健性的分类器 。
SVM可以通过引入核函数进行非线性分类。
2.SVM基本介绍
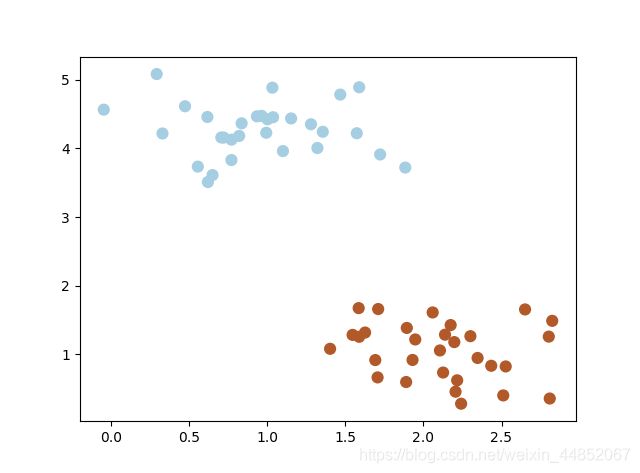
情景引入:给定一些分属于两个类别的数据,如使使用一个线性分类器,将这些数据分开来?
#导包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
# 画图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=plt.cm.Paired)
plt.show()
数据分布如下图:
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')
plt.show()
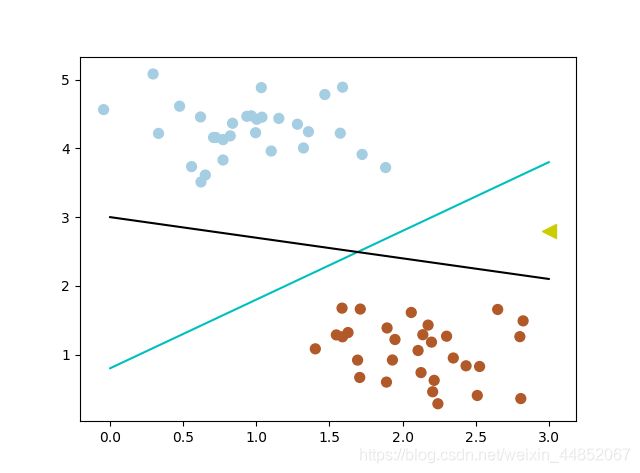
对于上图中的两种分类器,哪一个更好呢?
为了判断分类器的好坏,引入一个准则:好的分类器不仅仅是能够很好的分开已有的数据集,还能对未知数据集进行两个的划分。
假设,现在有一个属于红色数据点的新数据(3, 2.8) ,见下图,可以看到,此时黑色的线会把这个新的数据集分错,而蓝色的线不会。
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
plt.scatter([3], [2.8], c='#cccc00', marker='<', s=100, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')
plt.show()
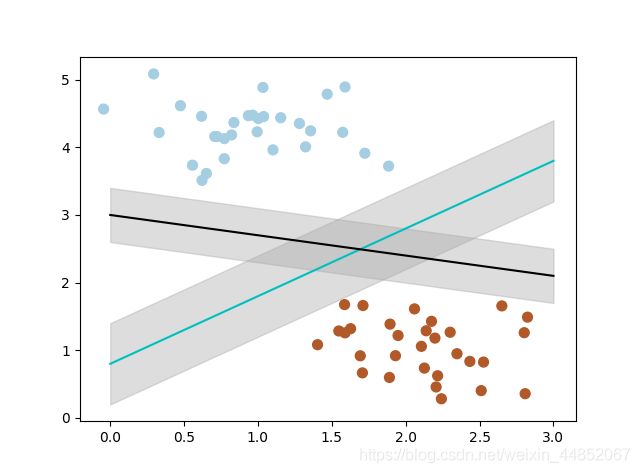
一般情况下,如何客观的评判两条线的健壮性呢?
最大间隔 最大间隔刻画着当前分类器与数据集的边界 。
以下面两个分类器为例:
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
# 画边距
plt.fill_between(x_fit, y_1 - 0.6, y_1 + 0.6, edgecolor='none', color='#AAAAAA', alpha=0.4)
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')
plt.fill_between(x_fit, y_2 - 0.4, y_2 + 0.4, edgecolor='none', color='#AAAAAA', alpha=0.4)
plt.show()
可以看到, 蓝色的线最大间隔是大于黑色的线的; 所以我们会选择蓝色的线作为我们的分类器。
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画图
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
# 画边距
plt.fill_between(x_fit, y_1 - 0.6, y_1 + 0.6, edgecolor='none', color='#AAAAAA', alpha=0.4)
plt.show()
此时问题来了:我们所选择的分类器是最优的分类器么?
为了找出最优分类器,我们需要引入我们今天的主角:SVM
from sklearn.svm import SVC
# SVM 函数
clf = SVC(kernel='linear')
clf.fit(X, y)
# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a*x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下界
b_down = clf.support_vectors_[0]
y_down = a* x_fit + b_down[1] - a * b_down[0]
# 最大边距 上界
b_up = clf.support_vectors_[-1]
y_up = a* x_fit + b_up[1] - a * b_up[0]
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
s=80, facecolors='none')
plt.show()
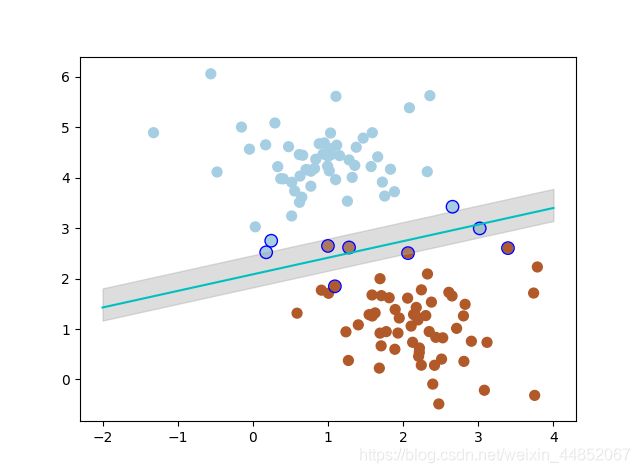
带黑边的点是距离当前分类器最近的点,我们称之为支持向量。
支持向量机为我们提供了在众多可能的分类器之间进行选择的原则,从而确保模型对未知数据集具有更高的泛化能力。
2.1 软间隔
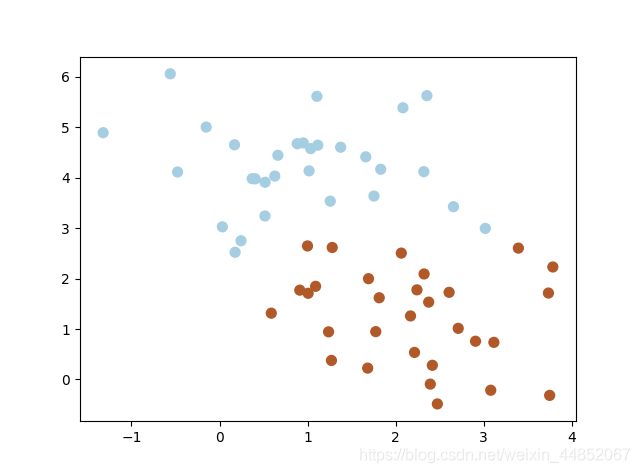
实际情景下,我们拿到的数据如下图所示:
from sklearn.datasets.samples_generator import make_blobs
import matplotlib.pyplot as plt
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
plt.show()
在上述这种情境下,并不容易找到最大间隔,如何解决这种情况下的分类问题?
我们此时引入软间隔,相比于硬间隔而言,我们允许个别数据出现在间隔带中 。
但是在软间隔中需要对分错的数据进行惩罚,SVC 函数中,有一个参数 C 就是惩罚参数。 惩罚参数越小,容忍性就越大。 以 C=1 为例子,比如说:
from sklearn.svm import SVC
import numpy as np
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
x_fit = np.linspace(-2, 4)
# 惩罚参数:C=1
clf = SVC(C=1, kernel='linear')
clf.fit(X, y)
# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a * x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下界
b_down = clf.support_vectors_[0]
y_down = a * x_fit + b_down[1] - a * b_down[0]
# 最大边距 上界
b_up = clf.support_vectors_[-1]
y_up = a * x_fit + b_up[1] - a * b_up[0]
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
s=80, facecolors='none')
plt.show()
当惩罚参数 C=0.2 时,SVM 会更具包容性,从而兼容更多的错分样本 :
from sklearn.svm import SVC
import numpy as np
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 惩罚参数:C=0.2
clf = SVC(C=0.2, kernel='linear')
clf.fit(X, y)
x_fit = np.linspace(-1.5, 4)
# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a * x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下界
b_down = clf.support_vectors_[10]
y_down = a * x_fit + b_down[1] - a * b_down[0]
# 最大边距 上界
b_up = clf.support_vectors_[1]
y_up = a * x_fit + b_up[1] - a * b_up[0]
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
s=80, facecolors='none')
plt.show()
2.2 超平面
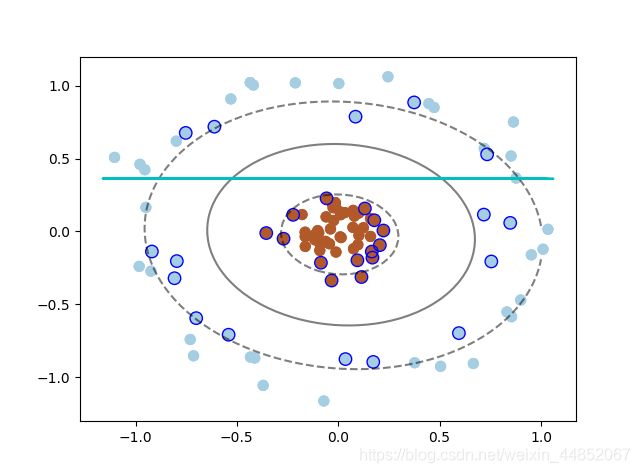
如果我们遇到这样的数据集,没有办法利用线性分类器进行分类,此时该如何解决这个问题?
我们引入超平面对数据进行更好的分类。
from sklearn.datasets.samples_generator import make_circles
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
# 画散点图
X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
clf = SVC(kernel='linear').fit(X, y)
# 最佳函数
x_fit = np.linspace(-1.5, 1.5)
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a*X - (clf.intercept_[0]) / w[1]
plt.plot(X, y_3, '-c')
plt.show()
可以将二维(低维)空间的数据映射到三维(高维)空间中从而进行正确的分类。
from mpl_toolkits.mplot3d import Axes3D
# 数据映射
r = np.exp(-(X[:, 0] ** 2 + X[:, 1] ** 2))
ax = plt.subplot(projection='3d')
ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap=plt.cm.Paired)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
x_1, y_1 = np.meshgrid(np.linspace(-1, 1), np.linspace(-1, 1))
z = 0.01*x_1 + 0.01*y_1 + 0.5
ax.plot_surface(x_1, y_1, z, alpha=0.3)
plt.show()
在 SVC 中,我们可以用高斯核函数来实现这以功能:kernel=‘rbf’ 来解决分线性分类问题。
# 画图
X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
clf = SVC(kernel='rbf')
clf.fit(X, y)
ax = plt.gca()
x = np.linspace(-1, 1)
y = np.linspace(-1, 1)
x_1, y_1 = np.meshgrid(x, y)
P = np.zeros_like(x_1)
for i, xi in enumerate(x):
for j, yj in enumerate(y):
P[i, j] = clf.decision_function(np.array([[xi, yj]]))
ax.contour(x_1, y_1, P, colors='k', levels=[-1, 0, 0.9], alpha=0.5,
linestyles=['--', '-', '--'])
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
s=80, facecolors='none')
plt.show()
3. SVM算法实战
3.1 库函数导入
# 基础函数库
import numpy as np
# 导入画图库
import matplotlib.pyplot as plt
import seaborn as sns
# 导入逻辑回归模型函数
from sklearn import svm
3.2 构建数据集并进行模型训练
# 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])
# 调用SVC模型 (支持向量机分类)
svc = svm.SVC(kernel='linear')
# 用SVM模型拟合构造的数据集
svc = svc.fit(x_fearures, y_label)
3.3 模型参数查看
# 查看其对应模型的w
print('the weight of Logistic Regression:',svc.coef_)
# 查看其对应模型的w0
print('the intercept(w0) of Logistic Regression:',svc.intercept_)
/"""
输出结果
the weight of Logistic Regression: [[ 0.33364706 0.33270588]]
the intercept(w0) of Logistic Regression: [-0.00031373]
"""/
3.4 模型预测
# 模型预测
y_train_pred = svc.predict(x_fearures)
print('The predction result:',y_train_pred)
# 输出结果
#The predction result: [0 0 0 1 1 1]
3.5 模型可视化
# 最佳函数
x_range = np.linspace(-3, 3)
w = svc.coef_[0]
a = -w[0] / w[1]
y_3 = a*x_range - (svc.intercept_[0]) / w[1]
# 可视化决策边界
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.plot(x_range, y_3, '-c')
plt.show()
对比之前的逻辑回归模型的决策边界,可以发现两个决策边界是有一定差异的(可以对比两者在X,Y轴上的截距),说明这两个不同在相同数据集上找到的判别线是不同的,原因其是由于两者选择的最优目标是不一致的。