『NLP学习笔记』Sklearn计算准确率、精确率、召回率及F1 Score

Sklearn计算准确率、精确率、召回率及F1 Score！

• 分类是机器学习中比较常见的任务，对于分类任务常见的评价指标有 准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1 score、ROC曲线(Receiver Operating Characteristic Curve)等。

一. 混淆矩阵

1.1. 混淆矩阵定义

• 首先需要知道混淆矩阵，混淆矩阵中的 P表示Positive，即正例或者阳性，N表示Negative，即负例 或者阴性。

1. TP(True Positive)： 表示 实际为正被预测为正 的样本数量。从英文名可以看出，首先是true，正确的，说明判断正确；再看后面的是Positive，正类，那么联系前文可知是判断正确的，即将正类判断为正类。
2. TN： 表示 实际为负被预测为负 的样本的数量。首先是True，判断正确；再看后者，Negative，负类，可以记忆为负类判断为负类。
3. FN： 表示 实际为正但被预测为负 的样本的数量。首先是False，错误的，说明判断错误；再看后者，Negative，负类，可以记忆为 将正类判断错误为负类。
4. FP(False Positive)： 表示 实际为负但被预测为正 的样本数量。首先是False，错误的，说明判断错误；再看后者，Positive，正类，那么联系前文可以记忆 将负类判断错误为正类。

• 另外：TP+FP表示所有被 预测为正的样本数量，同理FN+TN为所有被 预测为负的样本数量，TP+FN为 实际为正的样本数量，FP+TN为 实际为负的样本数量。

• 例如：下面例子中的混淆矩阵(11类别)：

• 下面给出了类别0的准确率、精确率、召回率、F1值计算方法。

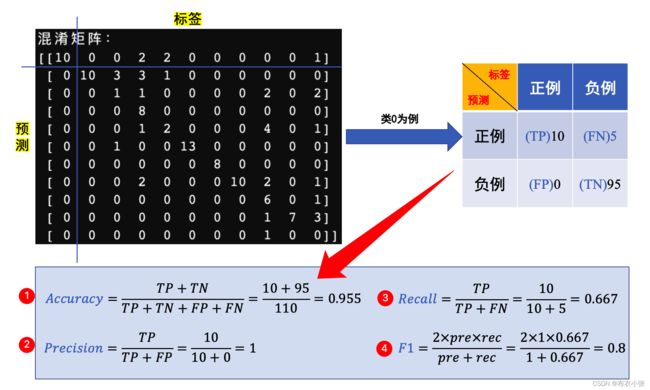
1.2. 例子演示

• Sklearn包中：

sklearn.metrics.confusion_matrix(y_true, y_pred, labels=None, sample_weight=None)
# y_true: 是样本真实分类结果
# y_pred: 是样本预测分类结果
# labels：是所给出的类别，通过这个可对类别进行选择
# sample_weight: 样本权重

• 官方例子1：

from sklearn.metrics import confusion_matrix

y_true=[2,1,0,1,2,0]
y_pred=[2,0,0,1,2,1]

C=confusion_matrix(y_true, y_pred)

# 结果如下
# array([[1, 1, 0],
#        [1, 1, 0],
#        [1, 0, 2]])

• 官方例子2：

y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
confusion_matrix(y_true, y_pred, labels=["ant", "bird", "cat"])

# 结果如下
# array([[2, 0, 0],
#        [0, 0, 1],
#        [1, 0, 2]])

二. 准确率

2.1. 准确率定义

• 准确率是分类正确的样本占总样本个数的比例，结合上面的混淆矩阵，公式可以这样写：
  $$\text{ Accuracy }=\frac{正确分类的样本个数}{总样本个数}=\frac{TP+TN}{TP+TN+FP+FN}\text{\hspace{1em}(1)}$$
• 准确率：是分类问题中最简单直观的评价指标，但存在明显的缺陷。比如如果样本中有99%的样本为正样本，那么分类器只需要一直预测为正，就可以得到99%的准确率，但其实际性能是非常低下的。也就是说，当不同类别样本的比例非常不均衡时，占比大的类别往往成为影响准确率的最主要因素。

• Sklearn函数接口的描述是这样的：
• 准确度分类得分
• 在多标签分类中，此函数计算子集精度：为样本预测的标签集必须完全匹配y_true（实际标签）中相应的标签集。
• 参数
• y_true: 一维数组，或标签指示符 / 稀疏矩阵，实际（正确的）标签.
• y_pred: 一维数组，或标签指示符 / 稀疏矩阵，分类器返回的预测标签.
• normalize: 布尔值, 可选的(默认为True). 如果为False，返回分类正确的样本数量，否则，返回正 确分类的得分.
• sample_weight: 形状为[样本数量]的数组，可选. 样本权重.
• 返回值
• score: 浮点型
• 如果normalize为True，返回正确分类的得分（浮点型），否则返回分类正确的样本数量（整型）.
  当normalize为True时，最好的表现是score为1，当normalize为False时，最好的表现是score未样本数量.

2.2. 例子演示

• 下面我们看一下sklearn中计算准确率的示例：

import numpy as np
from sklearn.metrics import accuracy_score

y_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
print(accuracy_score(y_true, y_pred))  # 0.5
print(accuracy_score(y_true, y_pred, normalize=False))  # 2

# 在具有二元标签指示符的多标签分类案例中
print(accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))))  # 0.5

• 需要注意的是最后一行代码中： y_true为$\left[\begin{array}{ll}0& 1\\ 1& 1\end{array}\right]$，y_pred为$\left[\begin{array}{ll}1& 1\\ 1& 1\end{array}\right]$，矩阵的 行表示样本，列表示标签(样本具有两个标签，标签0和1共同确定样本类别)，那么这时实际上只有一个样本是预测正确的，因此准确率为$\frac{1}{2}$，即0.5。
• 注意： 另外，因为准确率的缺陷比较明显，所以在多分类问题中一般不直接使用整体的分类准确率，而是 使用每个类别下的样本准确率的算术平均作为模型的评估指标。

• 混淆矩阵章节中的例子中，根据混淆矩阵可以计算出准确率为(主对角线上表示预测正确的样本数)：
  $$\text{ Accuracy }=\frac{正确分类的样本个数}{总样本个数}=\frac{75}{110}=0.682\text{\hspace{1em}(2)}$$

三. 精确率

3.1. 精确率定义

• 精确率指：模型预测为正的样本中实际也为正的样本占被预测为正的样本的比例。计算公式为：
  $$\text{ Precision }=\frac{预测为正中实际为正的样本数}{预测为正的样本数}=\frac{TP}{TP+FP}\text{\hspace{1em}(3)}$$

• Sklearn中的函数接口precision_score的描述如下：
• 一、计算精确率
• 精确率是$\frac{TP}{TP+FP}$的比例，其中 $TP$是预测为正&实际为正的数量，$FP$ 是实际为负&预测为正. 精确率直观地可以说是 分类器不将负样本标记为正样本的能力.
• 精确率最好的值是1，最差的值是0.
• 二、参数
• y_true : 一维数组，或标签指示符 / 稀疏矩阵，实际（正确的）标签.
• y_pred : 一维数组，或标签指示符 / 稀疏矩阵，分类器返回的预测标签.
• labels : 列表，可选值. 当average != binary时被包含的标签集合，如果average是None的话还包含它们的顺序. 在数据中存在的标签可以被排除，比如计算一个忽略多数负类的多类平均值时，数据中没有出现的标签会导致宏平均值（marco average）含有0个组件. 对于多标签的目标，标签是列索引. 默认情况下，y_true和y_pred中的所有标签按照排序后的顺序使用.
• pos_label : 字符串或整型，默认为1. 如果average = binary并且数据是二进制时需要被报告的类. 若果数据是多类的或者多标签的，这将被忽略；设置labels=[pos_label]和average != binary就只会报告设置的特定标签的分数.
• average : 字符串，可选值为 [None, ‘binary’ (默认), ‘micro’, ‘macro’, ‘samples’, ‘weighted’]. 多类或者多标签目标需要这个参数. 如果为None，每个类别的分数将会返回. 否则，它决定了数据的平均值类型.

1. ‘binary’: 仅报告由pos_label指定的类的结果. 这仅适用于目标(y_{true, pred})是二进制的情况.
2. ‘micro微观’: 通过计算总的真正性、假负性和假正性来全局计算指标.
3. ‘macro宏观’: 为每个标签计算指标，找到它们未加权的均值. 它不考虑标签数量不平衡的情况(常用).
4. ‘weighted’: 为每个标签计算指标，并通过各类占比找到它们的加权均值（每个标签的正例数）.它解决了’macro’的标签不平衡问题；它可以产生不在精确率和召回率之间的F-score.
5. ‘samples’: 为每个实例计算指标，找到它们的均值(只在多标签分类的时候有意义，并且和函数accuracy_score不同).
6. sample_weight : 形状为[样本数量]的数组，可选参数. 样本权重.

• 三、返回值
• precision : 浮点数(如果average不是None) 或浮点数数组, shape =[唯一标签的数量]
  二分类中正类的精确率或者在多分类任务中每个类的精确率的加权平均.

3.2. 例子演示

from sklearn.metrics import precision_score

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
print(precision_score(y_true, y_pred, average='macro'))  # 0.2222222222222222
print(precision_score(y_true, y_pred, average='micro'))  # 0.3333333333333333
print(precision_score(y_true, y_pred, average='weighted'))  # 0.2222222222222222
print(precision_score(y_true, y_pred, average=None))  # [0.66666667 0.     0.      ]

• 直接看函数接口和示例代码还是让人有点云里雾里的，我们这里先介绍两个与多分类相关的概念，再说说上面的代码是如何计算的。
• Macro[ˈmækroʊ]宏观 Average：宏平均是指在计算均值时使 每个类别具有相同的权重，最后结果是每个类别的指标的算术平均值。
• Micro Average：微平均是指计算多分类指标时 赋予所有类别的每个样本相同的权重，将所有样本合在一起计算各个指标。

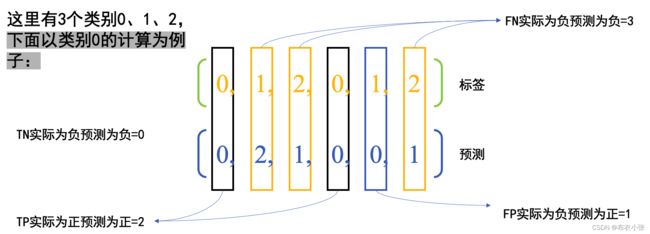
• 根据precision_score接口的解释，我们可以知道，当average参数为None时，得到的结果是每个类别的precision。上面的y_true有3个类别，分别为类0、类1、类2。我们将每个类别的TP、FP、FN列在下表中。

类别	TP(预测为正实际为正)	FP(实际为负预测为正)	FN(实际为正预测为负)	TN(实际为负预测为负)
类别0	2	1	0	3
类别1	0	2	2	2
类别2	0	1	2	3

• 那么每个类别的precision也就得到了，如下所示：
  $$P_0=\frac{预测为正中实际为正的样本数}{预测为正的样本数}=\frac{TP}{TP+FP}=\frac{2}{1+2}=\frac{2}{3}\approx 0.667$$$$P_1=\frac{预测为正中实际为正的样本数}{预测为正的样本数}=\frac{TP}{TP+FP}=\frac{0}{0+1}=0$$$$P_2=\frac{预测为正中实际为正的样本数}{预测为正的样本数}=\frac{TP}{TP+FP}=\frac{0}{0+1}=0\text{\hspace{1em}(4)}$$
• 从而 Macro Precision(宏观精确率) 也就知道了，就是$$\left(P_0+P_1+P_2\right)/3=2/9\approx 0.222\text{\hspace{1em}(5)}$$
• Micro Precision(微观精确率) 的计算要从每个样本考虑，所有样本中预测正确的有两个，那么TP就是2，剩下的4个预测结果都可以看做FP (补充：①可以这样理解分子是每个类别的TP加到一起，分母是每个类别的TP+FN；②也可以直接计算总样本的TP，也就是实际为正预测为正，剩余的样本就是FP，实际为负，预测为正。注意这个时候精确率值和召回率的值相等)，那么结果就是
  $$2/(2+4)=1/3\approx 0.333\text{\hspace{1em}(6)}$$
• 最后还有一个 average='weighted’ 的情况，因为这里每个类别的数量都恰好占比1/3，所以结果是
  $$P_w=\frac{1}{3}\times P_0+\frac{1}{3}\times P_1+\frac{1}{3}\times P_2\approx 0.222\text{\hspace{1em}(7)}$$

3.3. 宏平均和微平均的关系

• 虽然，我们是主要讲精确率的，但是 宏平均和微平均的概念也很重要，这里顺便对比一下。

1. 如果每个类别的样本数量差不多，那么宏平均和微平均没有太大差异
2. 如果每个类别的样本数量差异很大，那么注重样本量多的类时使用微平均，注重样本量少的类时使用宏平均
3. 如果微平均大大低于宏平均，那么检查样本量多的类来确定指标表现差的原因
4. 如果宏平均大大低于微平均，那么检查样本量少的类来确定指标表现差的原因

四. 召回率

4.1. 召回率定义

• 召回率：指 实际为正的样本中被预测为正的样本所占实际为正的样本的比例。计算公式为：
  $$\text{ Recall }=\frac{实际为正中预测为正的样本数}{实际为正的样本数}=\frac{TP}{TP+FN}\text{\hspace{1em}(8)}$$
• sklearn中recall_score方法和precision_score方法的参数说明都是一样的，所以这里不再重复，只是把函数和返回值说明贴在下面：

• 计算召回率
• 召回率是比率tp / (tp + fn)，其中tp是真正性的数量，fn是假负性的数量. 召回率直观地说是分类器找到所有正样本的能力.
• 召回率最好的值是1，最差的值是0.
• 返回值
• recall : 浮点数(如果average不是None) 或者浮点数数组，shape = [唯一标签的数量]
• 二分类中正类的召回率或者多分类任务中每个类别召回率的加权平均值.

4.2. 例子演示

• 官方示例代码为：

from sklearn.metrics import recall_score

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
print(recall_score(y_true, y_pred, average='macro'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average='micro'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average='weighted'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average=None))  # [1. 0. 0.]

• Recall和Precision只有计算公式不同，它们average参数为’macro’，‘micro’，'weighted’和None时的计算方式都是相同的，具体计算可以使用上节列出来的TP、FP、FN表，这里不再赘述。
• 那么每个类别的Recall也就得到了，如下所示：
  $$R_0=\frac{实际为正中预测为正的样本数}{实际为正的样本数}=\frac{TP}{TP+FN}=\frac{2}{0+2}=1$$$$R_1=\frac{实际为正中预测为正的样本数}{实际为正的样本数}=\frac{TP}{TP+FN}=\frac{0}{0+2}=0$$$$R_2=\frac{实际为正中预测为正的样本数}{实际为正的样本数}=\frac{TP}{TP+FN}=\frac{0}{0+2}=0\text{\hspace{1em}(4)}$$
• 从而 Macro Recall(宏观召回率) 也就知道了，就是$$\left(R_0+R_1+R_2\right)/3=1/1\approx 0.333\text{\hspace{1em}(5)}$$
• Micro Precision(微观召回率) 的计算要从每个样本考虑，所有样本中预测正确的有两个，那么TP就是2，剩下的4个预测结果都可以看做FP，那么结果就是
  $$2/(2+4)=1/3\approx 0.333\text{\hspace{1em}(6)}$$
• 最后还有一个 average='weighted’ 的情况，因为这里每个类别的数量都恰好占比1/3，所以结果是
  $$P_w=\frac{1}{3}\times R_0+\frac{1}{3}\times R_1+\frac{1}{3}\times R_2\approx 0.333\text{\hspace{1em}(7)}$$

五. F1 Score

5.1. F1 score定义

• F1 score是精确率和召回率的调和平均值，> - 计算公式为：
  $$F1=\frac{2\times \text{ precision }\times \text{ recall }}{\text{ precision }+\text{ recall }}\text{\hspace{1em}(9)}$$
• Precision体现了模型对负样本的区分能力，Precision越高，模型对负样本的区分能力越强；
• Recall体现了模型对正样本的识别能力，Recall越高，模型对正样本的识别能力越强。
• F1 score是两者的综合，F1 score越高，说明模型越稳健。
• sklearn中f1_score方法和precision_score方法、recall_score方法的参数说明都是一样的，所以这里不再重复，只是把函数和返回值说明贴在下面：

• 计算召回率 计算F1 score，它也被叫做F-score或F-measure.
• F1 score可以解释为精确率和召回率的加权平均值.
• F1 score的最好值为1，最差值为0. 精确率和召回率对F1 score的相对贡献是相等的.
• 在多类别或者多标签的情况下，这是权重取决于average参数的对于每个类别的F1 score的加权平均值.
• 返回值
• f1_score : 浮点数或者是浮点数数组，shape=[唯一标签的数量]
• 二分类中的正类的F1 score或者是多分类任务中每个类别F1 score的加权平均.

5.2. 例子演示

• 官方示例代码为：

from sklearn.metrics import f1_score

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
print(f1_score(y_true, y_pred, average='macro'))  # 0.26666666666666666
print(f1_score(y_true, y_pred, average='micro'))  # 0.3333333333333333
print(f1_score(y_true, y_pred, average='weighted'))  # 0.26666666666666666
print(f1_score(y_true, y_pred, average=None))  # [0.8 0.  0. ]

参考文献

• 本文主要参考以下作者的文章，这里表示感谢！
• sklearn计算准确率、精确率、召回率、F1 score：https://blog.csdn.net/hfutdog/article/details/88085878
• sklearn中混淆矩阵（confusion_matrix函数）的理解与使用：https://blog.csdn.net/SartinL/article/details/105844832
• 4.4.2分类模型评判指标（一） - 混淆矩阵(Confusion Matrix)：https://blog.csdn.net/Orange_Spotty_Cat/article/details/80520839