pytorch入门（三）：一些进阶部分的原理和实现

为什么pytorch是动态的

简单来说，说因为pytorch传入的参数可以动态修改，我们甚至可以在循环里修改，

其次呢就是框架可以自动求导

具体是什么原理就不过多介绍了

gpu加速

mac用户不支持gpu这个东西，拜拜hiahiahia

简述

只有Nvidia厂家且支持cuda模块的gpu才可以加速（amd yes不了了）

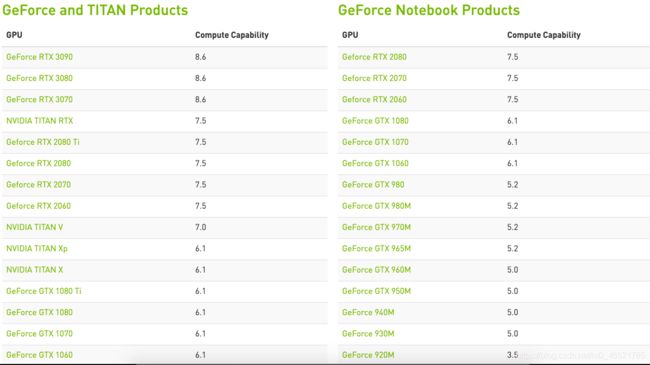
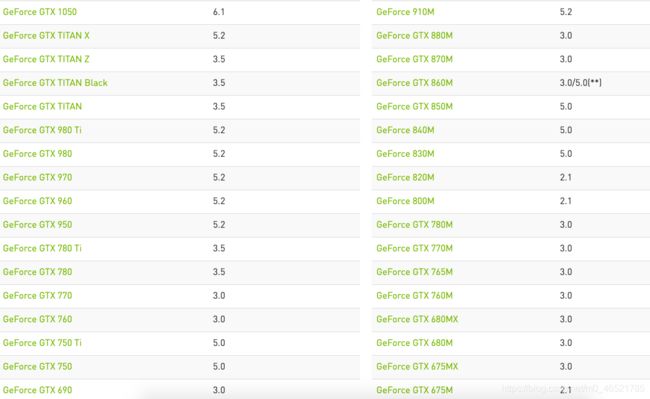
我们可以在官网查看https://developer.nvidia.com/cuda-gpus

常见的就geforce了，部分型号截图如下

如何安装cuda

首先，去官网下载cudahttps://developer.nvidia.com/cuda-toolkit-archive然后安装就一路默认即可。

其次就是配置环境变量

在终端输入nvcc -v（大写的v）查看是否安装成功

如果没成功就是环境变量配置的不对或者没安装显卡驱动，成功了就来官网下载cudnnhttps://developer.nvidia.com/cudnn，下载的CUDNN的版本要跟CUDA版本一致

选择cuda，重新安装pytorch-gpu

运行下面代码查看是否ok了
如果没成功就继续往下看，成功了恭喜你可以转身走了

import torch
print(torch.cuda.is_available())

来官网https://www.nvidia.cn/Download/index.aspx?lang=cn安装NVIDIA控制面板，键打开NIVIDIA控制面板，选择管理3D设置，全局设置中选择高性能NVIDIA处理器即可。

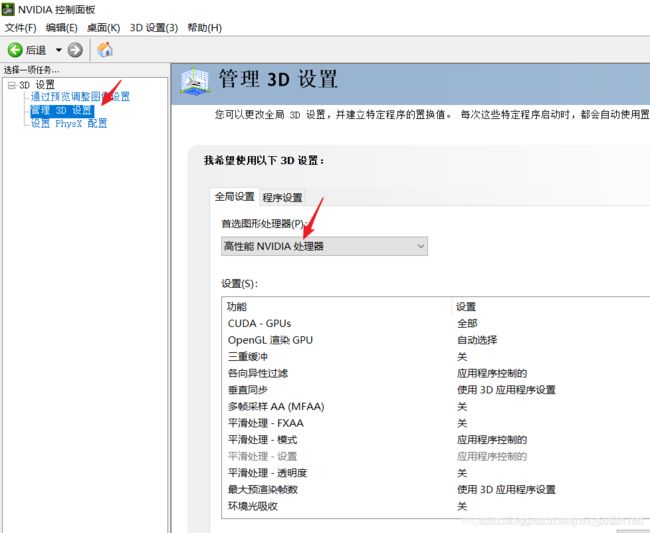
若还返回False的话 ，记得重启一下电脑，遇到问题重启一下电脑，看是否可以正常显示。

如何使用cuda加速

• 直接在数据/网络后面加上.cuda()即可把数据搬到gpu上

什么是过拟合

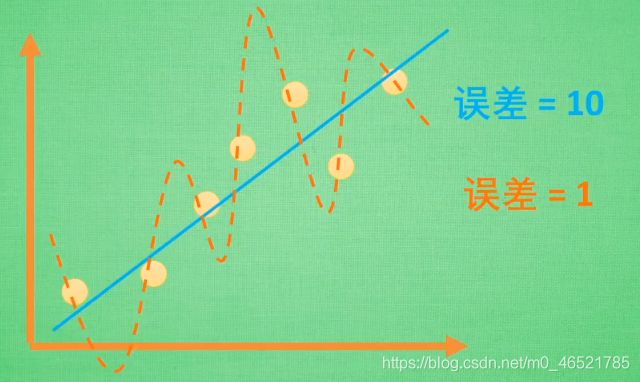
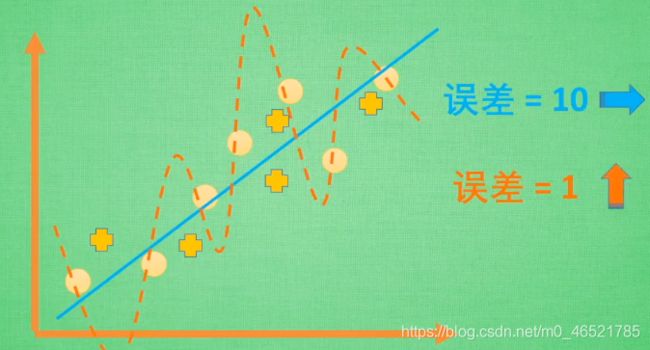
直白点说就是机器学习过于自信，已经到了自负的阶段了，表现就是在小圈子里表现的很好，大圈子里就处处碰壁

为了达到误差小的目的，机器学习可能会画出橙色的线

但如果实际数据是这样的，那机器学习的误差就超级大了

在分类问题上可能是这样的

那么如何解决过拟合现象呢？

• 增加数据量。（大多数情况下是因为数据量太少了）
• 使用正规化，我们把数据也考虑进来，当变化很大的时候，cost也很大，相当于一种惩罚机制
• 减少神经元的数量

（正规化公式）

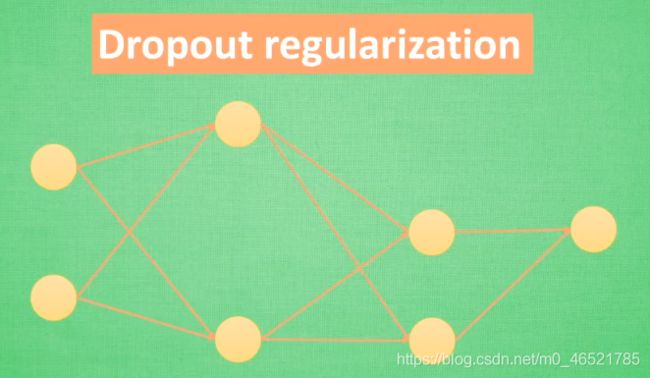
还有一种专门用于神经网络的正规化，我们在训练网络的时候随机忽略一些神经元让这个网络不完整，用不完整的神经元训练一次，第二次再随机忽略另外一些，这就可以让每次训练的时候，训练的结果都不会过于依赖某些特定的神经元。

机器学习是惩罚过大的w，神经网络直接是从根本上没有办法过于依赖w

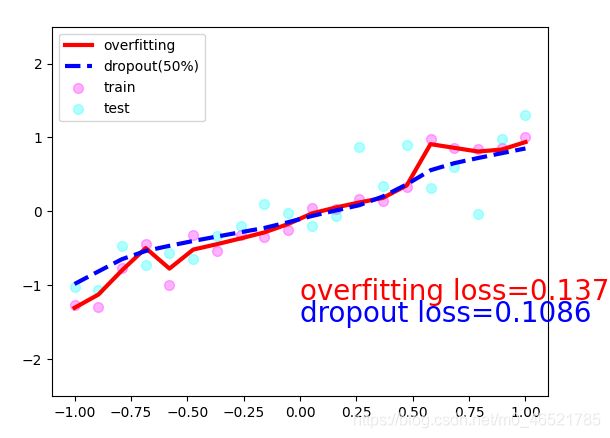
dropout处理过拟合

我们只需要加几个层就OK了，差别如图所示。

import torch
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

N_SAMPLES = 20
N_HIDDEN = 300

# training data
x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
y = x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))

# test data
test_x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
test_y = test_x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))

# show data
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test')
plt.legend(loc='upper left')
plt.ylim((-2.5, 2.5))
plt.show()

net_overfitting = torch.nn.Sequential(
    torch.nn.Linear(1, N_HIDDEN),
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, N_HIDDEN),
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, 1),
)

net_dropped = torch.nn.Sequential(
    torch.nn.Linear(1, N_HIDDEN),
    torch.nn.Dropout(0.5),  # drop 50% of the neuron
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, N_HIDDEN),
    torch.nn.Dropout(0.5),  # drop 50% of the neuron
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, 1),
)

print(net_overfitting)  # net architecture
print(net_dropped)

optimizer_ofit = torch.optim.Adam(net_overfitting.parameters(), lr=0.01)
optimizer_drop = torch.optim.Adam(net_dropped.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()

plt.ion()   # something about plotting

for t in range(500):
    pred_ofit = net_overfitting(x)
    pred_drop = net_dropped(x)
    loss_ofit = loss_func(pred_ofit, y)
    loss_drop = loss_func(pred_drop, y)

    optimizer_ofit.zero_grad()
    optimizer_drop.zero_grad()
    loss_ofit.backward()
    loss_drop.backward()
    optimizer_ofit.step()
    optimizer_drop.step()

    if t % 10 == 0:
        # change to eval mode in order to fix drop out effect
        net_overfitting.eval()
        net_dropped.eval()  # parameters for dropout differ from train mode

        # plotting
        plt.cla()
        test_pred_ofit = net_overfitting(test_x)
        test_pred_drop = net_dropped(test_x)
        plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.3, label='train')
        plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.3, label='test')
        plt.plot(test_x.data.numpy(), test_pred_ofit.data.numpy(), 'r-', lw=3, label='overfitting')
        plt.plot(test_x.data.numpy(), test_pred_drop.data.numpy(), 'b--', lw=3, label='dropout(50%)')
        plt.text(0, -1.2, 'overfitting loss=%.4f' % loss_func(test_pred_ofit, test_y).data.numpy(), fontdict={
     'size': 20, 'color':  'red'})
        plt.text(0, -1.5, 'dropout loss=%.4f' % loss_func(test_pred_drop, test_y).data.numpy(), fontdict={
     'size': 20, 'color': 'blue'})
        plt.legend(loc='upper left'); plt.ylim((-2.5, 2.5));plt.pause(0.1)

        # change back to train mode
        net_overfitting.train()
        net_dropped.train()

plt.ioff()
plt.show()

什么是批标准化（batch-normalization）

和普通标准化一样，批标准化就是将分散的数据统一的做法，也是优化神经网络的一种做法，可以让机器学习更容易学习到机器学习的规律

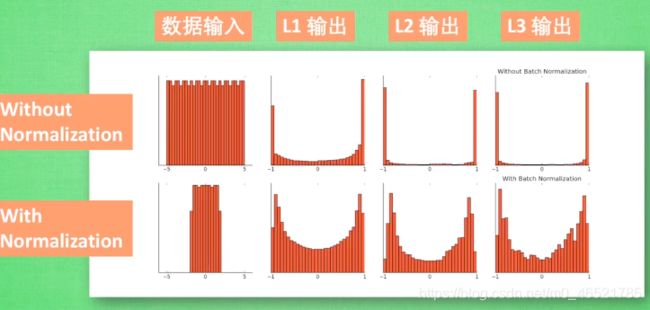
平常在数据分布或者隐藏层，激活一下，神经元不对数据大的特征敏感了，不论x再怎么大，激活到的数据增长的都很缓慢

将数据分为一块一块的，每次向前传递都会normalize一下。

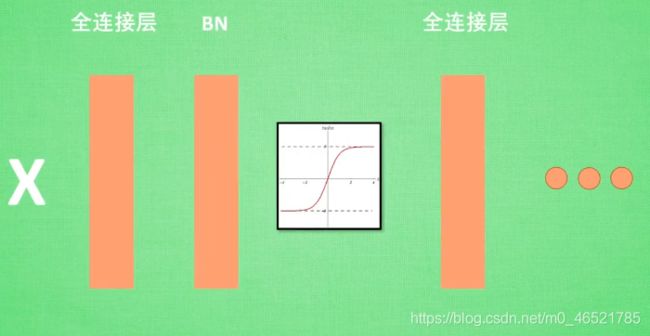
batch-normalization也可以看作成一个层面，在一层层添加神经网络的时候，先有x，再添加全连接层，再使用激活函数，再将数据传给下一个全连接层，我们把bn添加在全连接层和激励函数之间

下面是使用和未使用bn的分布，以及激活之后的数据

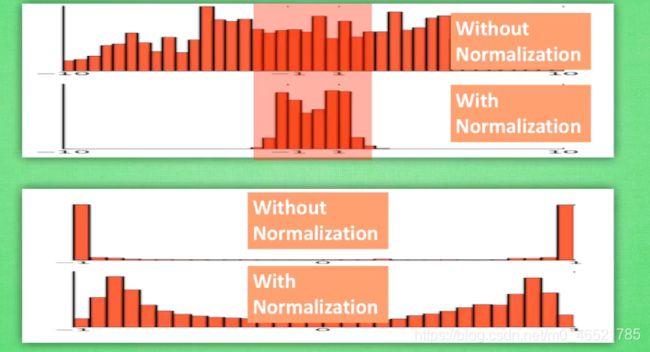
除此之外，bn不仅normalize了数据，还具有反向normalize的作用。当我们没有起到优化作用的时候，贝塔和伽马就会抵消一些normalize操作

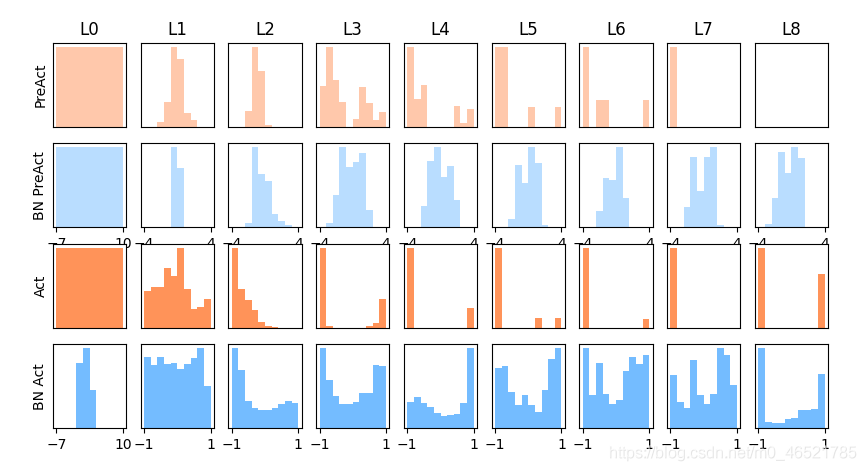
这是一张输出到最后的对比图

batch-normalization的实现

效果图，使用relu和tanh两种激活函数进行了对比

函数是nn.batchnorm1d(1,momentum=0.5)，1表示有多少个输入值

import torch
from torch import nn
from torch.nn import init
import torch.utils.data as Data
import matplotlib.pyplot as plt
import numpy as np
import matplotlib;matplotlib.use('tkagg')

# torch.manual_seed(1)    # reproducible
# np.random.seed(1)

# Hyper parameters
N_SAMPLES = 2000
BATCH_SIZE = 64
EPOCH = 12
LR = 0.03
N_HIDDEN = 8
ACTIVATION = torch.tanh
B_INIT = -0.2   # use a bad bias constant initializer

# training data
x = np.linspace(-7, 10, N_SAMPLES)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise

# test data
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise

train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x = torch.from_numpy(test_x).float()
test_y = torch.from_numpy(test_y).float()

train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)

# show data
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')


class Net(nn.Module):
    def __init__(self, batch_normalization=False):
        super(Net, self).__init__()
        self.do_bn = batch_normalization
        self.fcs = []
        self.bns = []
        self.bn_input = nn.BatchNorm1d(1, momentum=0.5)   # for input data

        for i in range(N_HIDDEN):               # build hidden layers and BN layers
            input_size = 1 if i == 0 else 10
            fc = nn.Linear(input_size, 10)
            setattr(self, 'fc%i' % i, fc)       # IMPORTANT set layer to the Module
            self._set_init(fc)                  # parameters initialization
            self.fcs.append(fc)
            if self.do_bn:
                bn = nn.BatchNorm1d(10, momentum=0.5)
                setattr(self, 'bn%i' % i, bn)   # IMPORTANT set layer to the Module
                self.bns.append(bn)

        self.predict = nn.Linear(10, 1)         # output layer
        self._set_init(self.predict)            # parameters initialization

    def _set_init(self, layer):
        init.normal_(layer.weight, mean=0., std=.1)
        init.constant_(layer.bias, B_INIT)

    def forward(self, x):
        pre_activation = [x]
        if self.do_bn: x = self.bn_input(x)     # input batch normalization
        layer_input = [x]
        for i in range(N_HIDDEN):
            x = self.fcs[i](x)
            pre_activation.append(x)
            if self.do_bn: x = self.bns[i](x)   # batch normalization
            x = ACTIVATION(x)
            layer_input.append(x)
        out = self.predict(x)
        return out, layer_input, pre_activation

nets = [Net(batch_normalization=False), Net(batch_normalization=True)]

# print(*nets)    # print net architecture

opts = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]

loss_func = torch.nn.MSELoss()


def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
    for i, (ax_pa, ax_pa_bn, ax, ax_bn) in enumerate(zip(axs[0, :], axs[1, :], axs[2, :], axs[3, :])):
        [a.clear() for a in [ax_pa, ax_pa_bn, ax, ax_bn]]
        if i == 0:
            p_range = (-7, 10);the_range = (-7, 10)
        else:
            p_range = (-4, 4);the_range = (-1, 1)
        ax_pa.set_title('L' + str(i))
        ax_pa.hist(pre_ac[i].data.numpy().ravel(), bins=10, range=p_range, color='#FF9359', alpha=0.5);ax_pa_bn.hist(pre_ac_bn[i].data.numpy().ravel(), bins=10, range=p_range, color='#74BCFF', alpha=0.5)
        ax.hist(l_in[i].data.numpy().ravel(), bins=10, range=the_range, color='#FF9359');ax_bn.hist(l_in_bn[i].data.numpy().ravel(), bins=10, range=the_range, color='#74BCFF')
        for a in [ax_pa, ax, ax_pa_bn, ax_bn]: a.set_yticks(());a.set_xticks(())
        ax_pa_bn.set_xticks(p_range);ax_bn.set_xticks(the_range)
        axs[0, 0].set_ylabel('PreAct');axs[1, 0].set_ylabel('BN PreAct');axs[2, 0].set_ylabel('Act');axs[3, 0].set_ylabel('BN Act')
    plt.pause(0.01)


if __name__ == "__main__":
    f, axs = plt.subplots(4, N_HIDDEN + 1, figsize=(10, 5))
    plt.ion()  # something about plotting
    plt.show()

    # training
    losses = [[], []]  # recode loss for two networks

    for epoch in range(EPOCH):
        print('Epoch: ', epoch)
        layer_inputs, pre_acts = [], []
        for net, l in zip(nets, losses):
            net.eval()              # set eval mode to fix moving_mean and moving_var
            pred, layer_input, pre_act = net(test_x)
            l.append(loss_func(pred, test_y).data.item())
            layer_inputs.append(layer_input)
            pre_acts.append(pre_act)
            net.train()             # free moving_mean and moving_var
        plot_histogram(*layer_inputs, *pre_acts)     # plot histogram

        for step, (b_x, b_y) in enumerate(train_loader):
            for net, opt in zip(nets, opts):     # train for each network
                pred, _, _ = net(b_x)
                loss = loss_func(pred, b_y)
                opt.zero_grad()
                loss.backward()
                opt.step()    # it will also learns the parameters in Batch Normalization

    plt.ioff()

    # plot training loss
    plt.figure(2)
    plt.plot(losses[0], c='#FF9359', lw=3, label='Original')
    plt.plot(losses[1], c='#74BCFF', lw=3, label='Batch Normalization')
    plt.xlabel('step');plt.ylabel('test loss');plt.ylim((0, 2000));plt.legend(loc='best')

    # evaluation
    # set net to eval mode to freeze the parameters in batch normalization layers
    [net.eval() for net in nets]    # set eval mode to fix moving_mean and moving_var
    preds = [net(test_x)[0] for net in nets]
    plt.figure(3)
    plt.plot(test_x.data.numpy(), preds[0].data.numpy(), c='#FF9359', lw=4, label='Original')
    plt.plot(test_x.data.numpy(), preds[1].data.numpy(), c='#74BCFF', lw=4, label='Batch Normalization')
    plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='r', s=50, alpha=0.2, label='train')
    plt.legend(loc='best')
    plt.show()

nice

yeap，基础入门部分已经完结，后面会补充概念和常见的问题嘿嘿