模式识别（一）

背景

基于提供的数据进行作业的分析。并假定男生、女生的身高、体重、鞋码、50m成绩、肺活量都服从正态分布。

作业内容

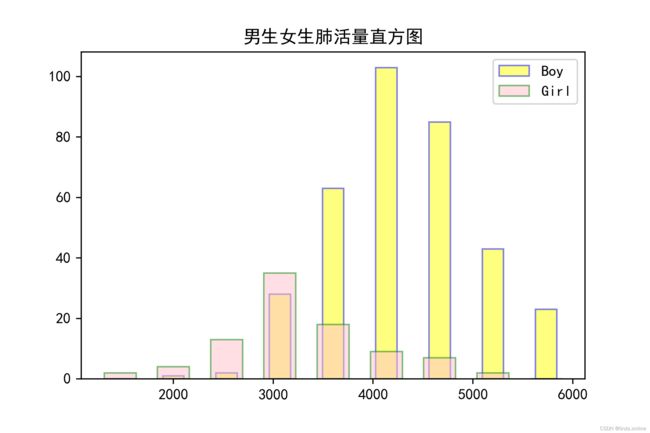
1. 以肺活量为例，画出男女生肺活量的直方图并做对比；

2. 采用最大似然估计方法，求男女生肺活量的分布参数；

3. 采用贝叶斯估计方法，求男女生肺活量的分布参数（方差已知，注明自己选定的参数情况）；

4. 基于身高和体重，采用最小错误率贝叶斯决策，画出类别判定的决策面。并判断某样本的身高体重分别为(165,50)时应该属于男生还是女生？为(175,55)时呢？

一、理论分析

1、最大似然估计方法估计分布参数

根据题目情景，假设男女生的肺活量服从正态分布，进行抽象之后也就是我们用最大似然的方法去估计单变量正态分布的均值和方差两个参数。

假设变量服从正态分布如下：
$$p(x\mid \mu )=\frac{1}{\sqrt{2\pi }\sigma }\exp \left[-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2\right]$$
则似然函数为：
$$\prod _{k=1}^{N}p\left(x_k\mid \mu \right)={\left(\frac{1}{2\pi {\sigma }^2}\right)}^{\frac{N}{2}}\exp \sum _{k=1}^N-\frac{{\left(x_k-\mu \right)}^2}{2{\sigma }^2}$$
取对数并对 $\mu$ 求导，令导函数为零即可求得对 $\mu$ 的最大似然估计
$$\begin{array}{l}\ln {\prod }_{k=1}^{N}p\left(x_k\mid \mu \right)=\frac{N}{2}\ln \frac{1}{2{\sigma }^2}-{\sum }_{k=1}^N\frac{{\left(x_k-\mu \right)}^2}{2{\sigma }^2}\\ \text{令}\frac{\partial \ln {\prod }_{k=1}^{N}p\left(x_k\mid \mu \right)}{\partial \mu }=0+\frac{1}{{\sigma }^2}{\sum }_{k=1}^N\left(x_k-\mu \right)=0\\ \text{ 则 }\hat{\mu }=\frac{1}{N}{\sum }_{k=1}^N{x}_k\end{array}$$
同理，对 ${\sigma }^2$ 进行最大似然估计可得：
$${\hat{\sigma }}^2=\frac{1}{N}\sum _{k=1}^N{\left(x_k-\hat{\mu }\right)}^2$$

2、贝叶斯方法估计分布参数

根据题目情景，假设男女生的肺活量服从正态分布，进行抽象之后也就是我们用贝叶斯估计的方法去估计单随机变量x（服从正态分布，在本题中也就是我们的男女肺活量）的均值这个参数（假设随机变量 $x$ 的方差已知，取 ${\sigma }^2$）具体流程如下：

①首先定出先验概率，假设参数 $\mu$ 服从正态分布如下：
$$p(\mu )=\frac{1}{\sqrt{2\pi }{\sigma }_0}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_0}{{\sigma }_0}\right)}^2\right]$$
②导出 $\mu$ 的后验概率分布：
$$p(\mu \mid x)=\frac{p(x\mid \mu )p(\mu )}{{\int }_{\Theta }p(x\mid \mu )p(\mu )d\mu }$$
③分母中的积分项为归一化常数 ，则进一步化简后验表达式得：
$$\begin{array}{rl}p(\mu \mid x)& =C\ast p(x\mid \mu )p(\mu )\\ & =C\ast \left\{\prod _{i=1}^N\frac{1}{\sqrt{2\pi }\sigma }\exp \left[-\frac{1}{2}{\left(\frac{x_i-\mu }{\sigma }\right)}^2\right]\right\}\ast \left\{\frac{1}{\sqrt{2\pi }{\sigma }_0}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_0}{{\sigma }_0}\right)}^2\right]\right\}\\ & =C^{\prime }\ast \exp \left(-\frac{1}{2}\left(\left(\frac{N}{{\sigma }^2}+\frac{1}{{\sigma }_0^2}\right){\mu }^2-2\left(\frac{1}{{\sigma }^2}\sum _{k=1}^N{x}_i+\frac{{\mu }_0}{{\sigma }_0^2}\right)\mu \right)\right)\\ & {=}^{def}\frac{1}{\sqrt{2\pi }{\sigma }_N}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_N}{{\sigma }_N}\right)}^2\right]\end{array}$$
④对比指数项得：
$$\begin{array}{rl}{\mu }_N& =\frac{N{\sigma }_0^2}{N{\sigma }_0^2+{\sigma }^2}{\overline{\mu }}_N+\frac{{\sigma }^2}{N{\sigma }_0^2+{\sigma }^2}{\mu }_0\\ {\sigma }_N^2& =\frac{{\sigma }^2{\sigma }_0^2}{N{\sigma }_0^2+{\sigma }^2}\end{array}$$
其中 ${\overline{\mu }}_N=\frac{1}{N}{\sum }_{k=1}^N{x}_k$

⑤根据后验概率即可以导出 $\mu$ 的贝叶斯估计为随机变量 $\mu$ 的期望：
$$\begin{array}{rl}\hat{\mu }& =\int \mu p(\mu \mid x)d\mu \\ & =\int \mu \frac{1}{\sqrt{2\pi }{\sigma }_N}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_N}{{\sigma }_N}\right)}^2\right]d\mu \\ & ={\mu }_N\\ & =\frac{N{\sigma }_0^2}{N{\sigma }_0^2+{\sigma }^2}{\overline{\mu }}_N+\frac{{\sigma }^2}{N{\sigma }_0^2+{\sigma }^2}{\mu }_0\end{array}$$

3、决策面求解

决策面的求解问题实际上是要求我们去设计一个分类器，对于最小错误率贝叶斯决策来说，具体流程如下：

①求出决策规则函数：
$$g_i(x)=p\left(x\mid w_i\right)p\left(w_i\right)$$
其中，$x$ 代表的是随机变量（可以是一个特征向量，表示一个样本拥有多个特征）； $g_i(x)$ 代表判别 $x$ 属于第 $i$ 类的决策规则函数；$w_i$代表的是随机变量第 $i$ 个类； $p(x|w_i)$ 是一个联合高斯分布：
$$p\left(x\mid w_i\right)=\frac{1}{{(2\pi )}^{d/2}{\left|{\mathrm{\Sigma }}_i\right|}^{1/2}}\exp \left[-\frac{1}{2}{\left(x-{\mu }_i\right)}^T\sum {}_i{}^{-1}\left(x-{\mu }_i\right)\right]$$
注意：$${\sum }_i$$ 为特征向量 $x$ 的协方差矩阵

②对判别函数取对数（不会改变判变规则函数的单调性）：
$$g_i(x)=\ln \left[p\left(x\mid w_i\right)p\left(w_i\right)\right]=-\frac{1}{2}{\left(x-{\mu }_i\right)}^T\sum {}_i{}^{-1}\left(x-{\mu }_i\right)-\frac{d}{2}\ln 2\pi -\ln \frac{1}{2}\left|{\Sigma }_i\right|+\ln p\left(w_i\right)$$
③导出决策方程为：
$$\begin{array}{c}{g}_i(x)-g_j(x)=0\\ \text{ 即 }{g}_i(x)-g_j(x)=-\frac{1}{2}\left[{\left(x-{\mu }_i\right)}^T{\Sigma }_i^{-1}\left(x-{\mu }_i\right)-{\left(x-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x-{\mu }_j\right)\right]-\ln \frac{1}{2}\frac{\left|{\Sigma }_i\right|}{\left|{\Sigma }_j\right|}+\ln \frac{p\left(w_i\right)}{p\left(w_j\right)}=0\end{array}$$

二、工程实现

1、数据清洗

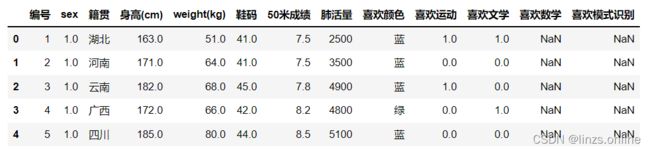
使用python中的pandas库导入原始数据，并简要查看具体内容，如下图1：

data = pd.read_excel('作业数据_2021合成.xls')
data.to_csv("data.csv",encoding="gbk")
data.head()

图 1 原始数据读取

使用 info( ) 函数查看原始数据基本属性，如下图2：

图 2 原始数据表格基本属性

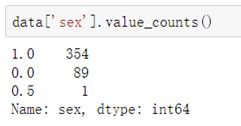
可以看到有些特征值是空的，所以要对数据进行清洗。首先查看男女性别这一列数据是否正常，如下图3：

图 3 男女性别统计

可以看到该列数据中有一个异常数据，可能是同学填写错误，下面使用随机森林的方法用“体重”和“身高”这两个特征去预测出该同学的性别，如下图4：

warnings.filterwarnings("ignore")
for i in range(len(data['sex'])):
    if( data.loc[:,'sex'].values[i] == 0.5):
        errorindex = i;
print("性别信息错误的同学所在的行序号为：",errorindex)
sexunknown = data.loc[errorindex,:]
sexknown = data.drop(labels=errorindex , axis = 0) #删除缺失数据的那一行
sexknown_x = sexknown.drop('sex',axis= 1)
sexknown_x = sexknown_x.loc[:,['weight(kg)','鞋码']]
sexknown_y = sexknown['sex']
sexunknown_x = sexunknown.drop(['sex'])
sexunknown_x=sexunknown_x.loc[['weight(kg)','鞋码']]
print("用随机森林的方法根据‘体重’‘鞋码’这两个特征预测该同学的性别")
from sklearn.ensemble import RandomForestRegressor
rfr=RandomForestRegressor(random_state=None,n_estimators=1000,n_jobs=-1)
rfr.fit(sexknown_x,sexknown_y)
print("训练得到的模型得分为：",rfr.score(sexknown_x,sexknown_y))
sexunknown_y = rfr.predict([sexunknown_x])
if sexunknown_y >= 0.5:
    sexunknown_y = 1
else:
    sexunknown_y = 0
print("用该模型预测得到该同学的性别值为：",sexunknown_y)
data.loc[errorindex,"sex"] = sexunknown_y
data['sex'].value_counts().plot.pie(autopct = '%1.2f%%',)
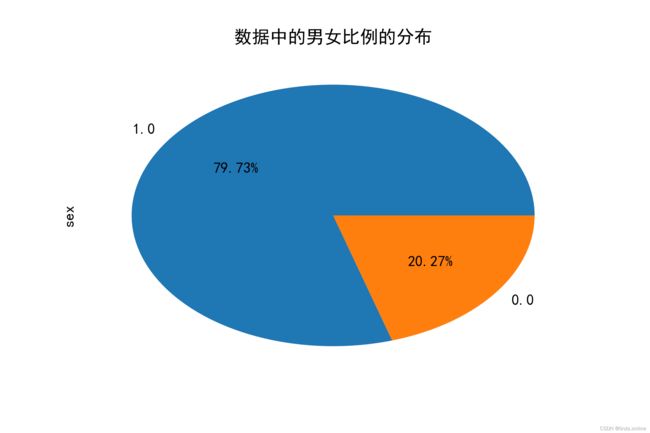
plt.title("数据中的男女比例的分布")

图 4 使用随机森林的预测结果替换异常数据

由上图4可知，我们通过随机森林的方法去预测出该异常数据可以知道该名同学的性别应该是女生，下面再次进行统计得到男女比例大概为4：1，如下图5：

图 5 数据中的男女生比例

同样地，我们在数据中发现在“肺活量”一列中也有三个异常数据，其中有两个是空值，有一个是字符输入，我们同样使用随机森林的方法，用“鞋码”“性别”这两个特征去预测出这三名同学的肺活量，结果如下图6所示：

图 6 肺活量异常数据处理

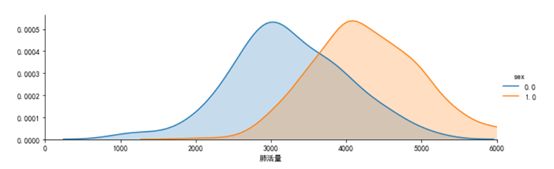
用预测值替换掉异常数据，之后绘制男女生的肺活量值分布如下图7所示：

图 7 男女生肺活量分布大致情况

由上图可以看到男女生的肺活量基本服从正态分布，而且男生的肺活量均值比女生的肺活量均值要高一些。

2、 直方图绘制

根据男女生的肺活量数据，直接绘制他们的直方图如下图8所示：

图 8 男女生肺活量直方图

由上图可以看到，男女生的肺活量值大致服从正态分布，男生肺活量的均值在4200左右，女生肺活量均值在3200左右。

3、 最大似然估计方法估计参数

根据上面的理论分析可以得知，最大似然估计方法去估计参数，对于正态分布来说，实际上最后的均值的估计值就是等于样本的均值，方差的估计值等于样本二阶中心矩
$$\begin{array}{rl}\hat{\mu }& =\frac{1}{N}\sum _{k=1}^N{x}_k\\ {\hat{\sigma }}^2& =\frac{1}{N}\sum _{k=1}^N{\left(x_k-\hat{\mu }\right)}^2\end{array}$$
下面展示python中集成函数的求解结果：

# 最大似然估计
girl_vcmean_mle, girl_vcstd_mle = norm.fit(Gir_vitalCapacity)
boy_vcmean_mle, boy_vcstd_mle = norm.fit(Boy_vitalCapacity)
print("最大似然估计男生的肺活量参数为：均值{},方差{}\n".format(boy_vcmean_mle,boy_vcstd_mle**2))
print("最大似然估计女生的肺活量参数为：均值{},方差{}\n".format(girl_vcmean_mle,girl_vcstd_mle**2))

图 9 python实现最大似然估计男女生肺活量分布参数

从估计结果可以看到男生肺活量均值为4310，女生肺活量均值为3235，符合我们的认知。

4、 贝叶斯估计方法估计参数

根据上面的理论分析可以得知，贝叶斯估计方法去估计参数，对于正态分布来说，实际上最后的均值的估计值就是等于样本的均值和我们的先验均值的一个加权求和，在本次实验中我们对 $\hat{\mu }$ 参数的先验估计为一个正态分布。男生的均值取4500，方差取500；女生的均值取300，方差取500；假设整体数据的方差为500000（和最大似然估计的基本在一个水平上即可）
$$\begin{array}{rl}\hat{\mu }& =\int \mu p(\mu \mid x)d\mu \\ & =\int \mu \frac{1}{\sqrt{2\pi }{\sigma }_N}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_N}{{\sigma }_N}\right)}^2\right]d\mu \\ & ={\mu }_N\\ & =\frac{N{\sigma }_0^2}{N{\sigma }_0^2+{\sigma }^2}{\overline{\mu }}_N+\frac{{\sigma }^2}{N{\sigma }_0^2+{\sigma }^2}{\mu }_0\end{array}$$
Python代码实现如下图10所示：

# 贝叶斯估计
def bayesmean(data,priormean,priorvar,variance):
    return int(priorvar*sum(data)+variance*priormean)/(len(data)*priorvar+variance) 
boy_vcmean_bayes = bayesmean(Boy_vitalCapacity,4500,500,500000)
girl_vcmean_bayes = bayesmean(Gir_vitalCapacity,3000,500,500000)
print("贝叶斯估计男生的肺活量均值为：{}\n(参数分布的先验均值取{}，先验方差取{}，假设数据分布方差为{})\n".format(boy_vcmean_bayes,4500,500,500000))
print("贝叶斯估计女生的肺活量均值为：{}\n(参数分布的先验均值取{}，先验方差取{}，假设数据分布方差为{})".format(girl_vcmean_bayes,3000,500,500000))

图 10 python实现贝叶斯估计分布参数

由上图10中的python实现对男女生肺活量分布的均值估计可知，男生的肺活量均值为4450，女生的肺活量均值为3019，可见与最大似然估计基本一致，**只是这里估计出来的值往我们的先验值方向更靠近一些，说明贝叶斯估计融合了先验知识，**可见实验结果符合认知。

图 11 估计分布与真实数据分布对比

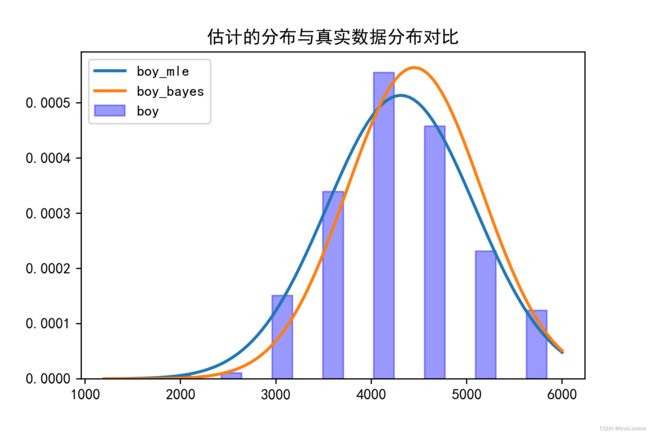
上图11是把男生的肺活量真实数据的分布（紫蓝色柱状图）与最大似然估计得到的分布（蓝色曲线）和贝叶斯估计得到的分布（橙色曲线）放在一起做一个对比，在图中可以看出三者基本一致，其中，最大似然估计得到的分布和原数据高度相似，这是因为从推导结果上来看，最大似然估计就是利用数据得到估计，没有融入任何先验知识，所以最大似然估计得到的结果就应该和原数据基本一致；而贝叶斯估计得到的分布没有和原数据高度相似，而是会贴近我们的先验估计，因为从推导结果表达式上来看，我们可以看到贝叶斯估计的参数实际上是样本的信息和先验的信息的一个加权组合，当我们的先验方差不大的时候估计得到的值就会更贴近先验值。

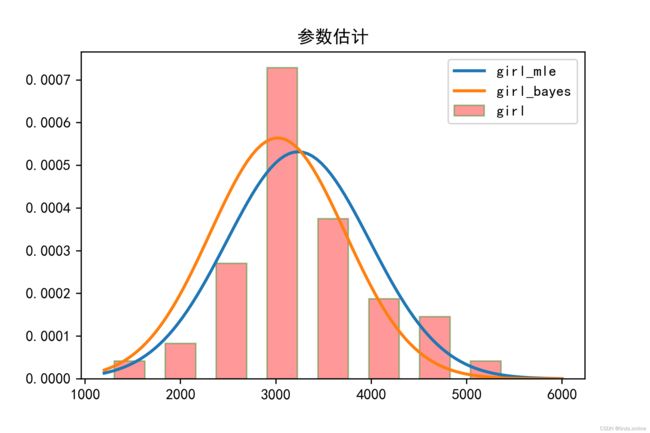
同样地，这里我们也画出女生的肺活量数据分布和估计得到的分布，如下图12:

图 12 女生肺活量数据分布与估计的分布对比

5、 决策面求解

在本题中利用“体重”“身高”这两个特征对样本中的同学性别进行分类，实际上抽象出来就是利用二维的特征向量数据对样本进行分类，对于决策面的求解，从上面的理论推导部分得到的推导结果就是方程： $g_i(x)-g_j(x)=0$ ，展开就是下面的式子：
$$g_i(x)-g_j(x)=-\frac{1}{2}\left[{\left(x-{\mu }_i\right)}^T{\Sigma }_i^{-1}\left(x-{\mu }_i\right)-{\left(x-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(x-{\mu }_j\right)\right]-\ln \frac{1}{2}\frac{\left|{\Sigma }_i\right|}{\left|{\Sigma }_j\right|}+\ln \frac{p\left(w_i\right)}{p\left(w_j\right)}=0$$
从上面的推导表达式来看，求得这样一个表达式我们需要得到样本中男生女生的“体重”和“身高”这两个特征的均值、男生女生的类概率以及他们的“体重”“身高”的协方差矩阵，因为这里的每个样本的特征向量都是二维的，所以协方差矩阵应该是 $2\times 2$ 的矩阵。下面表1中汇总了求解所需的信息。

表1 计算决策面所需信息

	男生	女生
特征均值$\left[{\mu }_{身高}，{\mu }_{体重}\right]$	$[174.31,67.59]$	$[163.13,51.21]$
类概率	0.80	0.20
特征向量的协方差矩阵	$\left[\begin{array}{cc}36.73& 42.27\\ 42.27& 154.15\end{array}\right]$	$\left[\begin{array}{cc}23.37& 14.28\\ 14.28& 35.95\end{array}\right]$

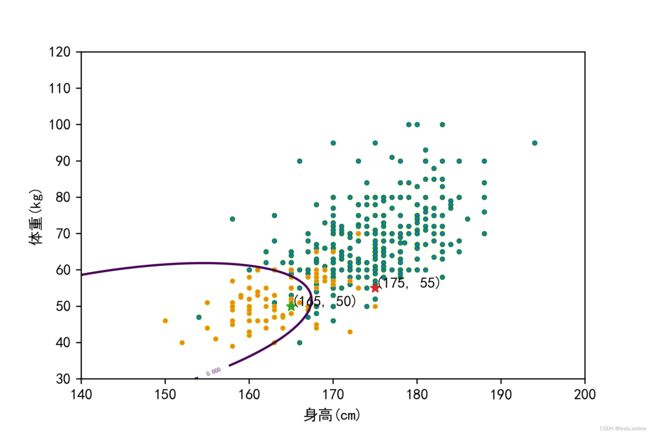
由求解到的决策面进行可视化得到如下图13：

图 13 男女生判别决策可视化

上图13中紫色曲线就是我们的决策方程，曲线下方的数据点就是样本数据中女生的“身高”“体重”样本点，曲线上方的数据点就是男生的“身高”“体重”样本点，由图可以看出我们计算出来的决策面基本可以正确划分男女类别，符合理论推导。