1.问题引入
从本周起正式进入cs61b的后半部分课程,数据结构,考虑一个问题:
现有一个有序数组,查找数组中是否有重复项算法1:逐项比较,比如A[0]分别与A[1],A[2],A[3]......A[n]比较,之后再从A[1]开始,与A[2],A[3]....A[n]比较,A[2]与A[3],A[4]....比较,以此类推。
显然算法1并未充分利用数组有序性的特点,因此算法2:
由于数组是有序的,因此我们只需要比较相邻两项即可,重复的元素一定位于相邻两项。
即A[0]与A[1]比较,A[1]与A[2]比较,A[2]与A[3]比较....A[n-1]与A[n]比较。
使用Java实现以上两种算法,分别是
//算法1
public static boolean dup1(int[] A) {
for (int i = 0; i < A.length; i += 1) {
for (int j = i + 1; j < A.length; j += 1) {
if (A[i] == A[j]) {
return true;
}
}
}
return false;
}
//算法2
public static boolean dup2(int[] A) {
for (int i = 0; i < A.length - 1; i += 1) {
if (A[i] == A[i + 1]) {
return true;
}
}
return false;
}
那么现在的问题是:算法1与算法2哪个更好?判断标准是什么?
2.运行时间测量
在Linux下使用命令time 可实现程序运行时间的测量。我们的main()函数主要是分别对dup1()和dup2()调用:
public static void main(String[] args) {
int N = Integer.parseInt(args[0]);
int[] A = makeArray(N);
dup1(A); // dup2(A);
}
上图是dup1(),下图是dup2(),当数组大小为200000 时,对比运行时间可知dup2()明显快很多,
当数组大小为1000000时,dup1()直接TLE了,dup2()依然可以很快得出结果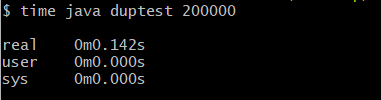
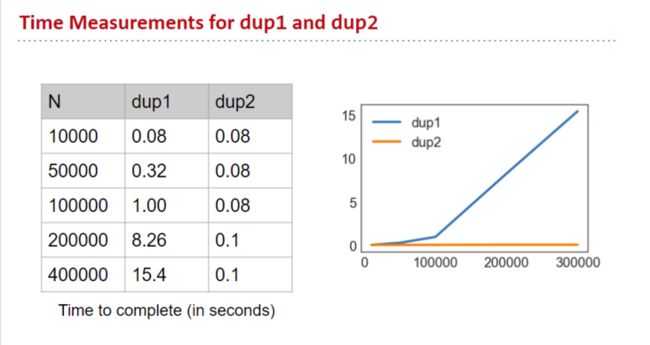
但是事实上仅凭运行时间得出的结果只是给人一种直观的感受,算法2更快,时间测量的方法必须基于同一台机器上,不同的电脑性能不同,运行时间也会不同,设想一下在超级计算机上运行dup1(),依然可以相对较快。
3.衡量计算成本
现在我们考虑以一种新的方式来衡量两种算法的运行时间,即分析程序的每一条代码操作的执行次数,为何这样考虑更优?是因为无论在哪台机器上运行这两个函数dup1()与dup2(),其代码执行次数是一定的,与机器性能优劣无关,更加科学。
算法1
显然,线性函数与抛物线相比,前者更优,以上执行次数公式是josh直接给出的,后续会有详细
介绍。
4.简化成本模型
事实上,在分析一个程序的计算成本时,不必考虑如此细致,可做以下简化:
Simplifications:
- 只考虑最坏情况
- 选择最具代表性的操作
- 忽略低阶函数和常数系数
算法处理规模十分重要!最坏的情况往往最具有代表性,当程序的任务处理量很少时,在现代计算机上,一秒能够执行1e8的任务量,此时无论你选择哪种算法都影响不大,但是当任务量极大时,算法的优劣则体现出来了,好的算法能够快速执行完程序并反馈给用户,而劣式算法会花费数以千计的时间。
让我们重新对dup1()进行估计:
- 选取最具代表性的操作,例如:
- 增量 +=1(其实并非最具代表性) 代码执行次数是 1 to \( (N^2+N)/2 \)
- 考虑最坏情况: \( (N^2+N)/2 \)
- 忽略常数系数与低阶函数: \( N^2 \)
5.精确得出代码执行次数
上面我们是直接给出的操作的执行次数,可能初学者不太理解如何得出,因此这次我们精确地给出数学公式的表达。
选取最具代表性操作:
$$ if (A[i] == A[j]) $$
即 == 操作,再一次对dup1()进行估计,可以分别列出i与j的取值方阵,寻找规律(也可以根据代码直接分析出来,如i = 0, j = 1,2,......N-1)
几何直观估计
在几何直观上,==的操作次数即蓝色区域三角形的面积: \(N^2/2\)
6.Big-Theta
定义:
$$ R(n)\in \Theta(f(n)) $$
表示存在两个数\(k_{1},k_{2}\),对所有\(N > N_{0}\) ,有:
$$ k_{1}\cdot f(n) \le R(n) \le k_{2}\cdot f(n) $$
即\(\Theta(f(N))\)的含义是\(R(N)\)属于\(f(N)\)的函数簇
Example:
\( 40 sin(N) + 4N^2 ∈ Θ(N^2) \)
\( R(N) = 40 sin(N) + 4N^2 \)
\( f(N) = N^2 \)
k1 = 3
k2 = 5
7.Big-O
定义:
$$ R(n)\in O(f(n)) $$
表示存在\(k_{2}\),对所有\(N > N_{0}\) ,有:
$$ R(n) \le k_{2}\cdot f(n) $$
即\(O(f(N))\)的含义是\(k_{2} \cdot f(N)\)是\(R(N)\)上界
Example:
\( 40 sin(N) + 4N^2 ∈ O(N^4) \)
\( R(N) = 40 sin(N) + 4N^2 \)
\( f(N) = N^4 \)
k2 = 1




