在时域频域的信号分析的过程中,一个常见的说法叫:频域数据补零会让时域数据内插。
意思是在频域数据中多补几个零,再做ifft(逆傅里叶变换)后的时域数据,会变得更加“细腻”,分辨率会更高。
关于频域补零让时域内插,我有一点朴素的理解:
- 频域数据已经包含了所有正弦波的信息,IFFT解出的时域数据是否细腻,只能看时域数据的点数是否够多。
- 做FFT/IFFT运算前后时域和频域的数据的点数是一样多的。
哦,是两点,基于这两点,我们只能把频域数据中原本不存在的高频信息中加上0,再转成时域信号,这样点数就够多呀。频域补零会让时域采样点增加。
基于这样朴素的认知,看看下面两张傅里叶级数的图:
补两个零:
以上,整个正弦波的周期时间没变,但是采样点多了,也就更"细腻"了。
这个网页的的源码在https://gist.github.com/kazad/8bb682da198db597558c
对于学习频域时域的直观感受有很强的帮助。但是因为众所周知的原因,里面的个别js脚本访问不了。我已经将其下载好,放在github地址: https://github.com/Binfun/fourier_transform
如果补的零再增加的话,那么这些点数就慢慢趋近于一个正常的正弦波了:
通过以上示例,仅仅是直观地理解频域补零->时域插值是没有问题的。
但是上面的例子还是有点儿“问题”
在FFT的世界中,上图的描述不准确,而是下图:
在实践过程中,对FFT后的频域结果,如果要补零则是补在中间(高频补零),再进行IFFT(逆傅里叶变换)转成时域。 知道这句话则足够了,以下内容,则是我对于这个现象的朴素的解释。
这个时候我们又不得不拿出那个之前聊过的概念:负频率。
在上两图中,四个点的频域数据,2HZ和-2Hz是一回事,3Hz和-1Hz也是一回事。
就像观察一座山,3Hz是顺时针,沿着东南西北方向去观察,-1Hz是逆时针,分别从东北西南方向去看。但是3Hz每次转换方向时,步进是三个方向,一开始是东,顺时针转动三个方向变成了北,再转动三次变成了西,最后变成了南,最后也是东北西南四个方向观察,那么-1Hz是逆时针步进一个方向,也是东北西南。
在DFT/FFT计算3Hz时,根据DFT的公式,会计算相位点(数字都会乘以2pi,为方便显示,以下省略2pi):
[0,-3/4, -6/4, -9/4]。该序列可以看作是,顺时针依次递增3/4个2pi。所以它可以看做是3Hz。
将序列[0,-3/4, -6/4, -9/4]中的整数去掉,一个整数就代表一个2pi,一个2pi就代表转动了一圈回到原点。
会得到[0,-3/4, -2/4, -1/4]。这样看序列的话,逆时针依次增加1/4个2pi,所以它可以看做是 -1Hz 。
如果频域数据的点数是N,假设任意一个点的正频率表示为A,那么其负频率表示就是A-N。
那么为什么FFT之后的频域数据,前半部分是以正频率表示,后半部分以负频率表示呢?
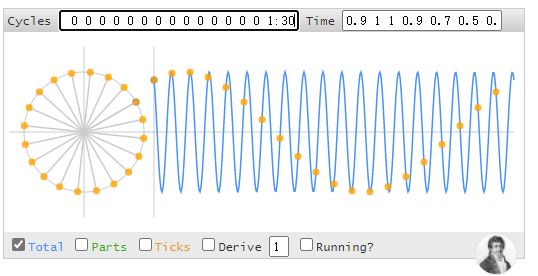
我们对1Hz的频点取个30度的初始相位(以1:30表示),然后在后面补零,此刻它是1Hz的正弦波:
我们对序列[0 1:30]中间插18个0,即数字1在序列的最后一位,此时序列有20个频点,最后一个频点正频率的角度是19Hz,负频率的角度是-1Hz。我们现在观察下图黄点连成的线,此刻它是一个 -1Hz的正弦波,并且也是30度的初始相位,而并非是19Hz。
可以把上面两张图结合起来看:
最后基于以上的实验,我朴素地再理解一下,在FFT的世界中,无法支撑起大于等于总点数一半的正频率,所以前半部分是正频率,后半部分是负频率。而高频的判断标准是其绝对值,所以高频在中间。