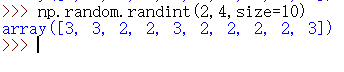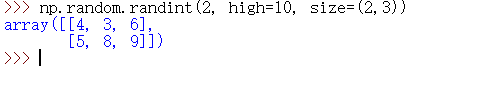遗传算法&代码小讲解
文章目录
- 前言
- 遗传算法
-
- 繁殖
- 交叉
- 变异
- 选择
- 代码编写
-
- “开挂的API”
-
- numpy.random.randint()
- 元素替换
- np.random.choice
- 代码结构
- 完整代码
- 总结
本博文优先在掘金社区发布!
前言
明天就除夕了,该过年了,所以明天就不更新博文了。那么本博文呢,是我无意中逛B站,然后发现这个UP主的一个关于遗传算法的视频的讲解(莫烦python),然后看了看他写的代码,然后对比了一下我的代码发现我的代码有不少可以优化的点。同时也是做一个小记录,细说一下实现遗传算法的步骤,以及一些在python当中可以直接开挂的写法(我先前写的代码是直接使用list实现的在很多部分的代码实现都在造轮子,淦~),然后代码也是以那个UP主的代码进行讲解,说明,优化。
那么首先我们要了解什么是遗传算法
遗传算法
遗传算法其实是在用计算机模拟我们的物种进化。其实更加通俗的说法是筛选,这个就和我们袁隆平老爷爷种植水稻一样。有些个体发育良好,有些个体发育不好,那么我就先筛选出发育好的,然后让他们去繁衍后代,然后再筛选,最后得到高产水稻。其实也和我们社会一样,不努力就木有女朋友就不能保留自己的基因,然后剩下的人就是那些优秀的人和富二代的基因,这就是现实呀。所以得好好学习,天天向上!
那么回到主题,我们的遗传算法就是在模拟这一个过程,模拟一个物竞天择的过程。
所以在我们的算法里面也是分为几大块
繁殖
首先我们的种群需要先繁殖。这样才能不断产生优良基于,那么对应我们的算法,假设我们需要求取
Y = np.sin(10 * x) * x + np.cos(2 * x) * x
的最大值(在一个范围内)那么我们的个体就是一组(X1)的解。好的个体就会被保留,不好的就会被pass,选择标准就是我们的函数 Y 。那么问题来了如何模拟这个过程?我们都知道在繁殖后代的时候我们是通过DNA来保留我们的基因信息,在这个过程当中,父母的DNA交互,并且在这个过程当中会产生变异,这样一来,父母双方的优秀基于会被保存,并且产生的变异有可能诞生更加优秀的后代。
所以接下来我们需要模拟我们的DNA,进行交叉和变异。
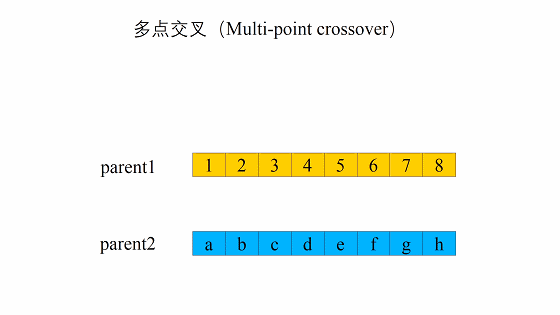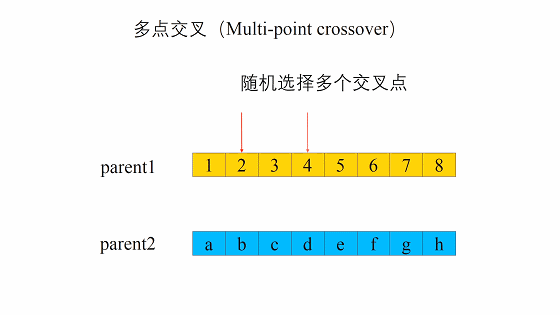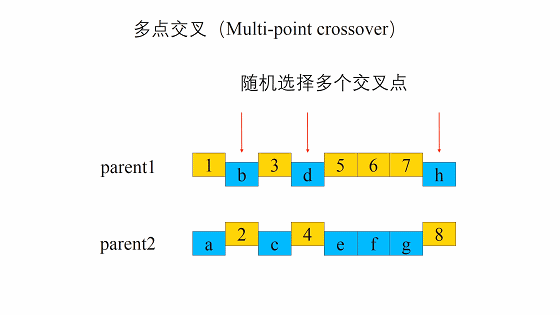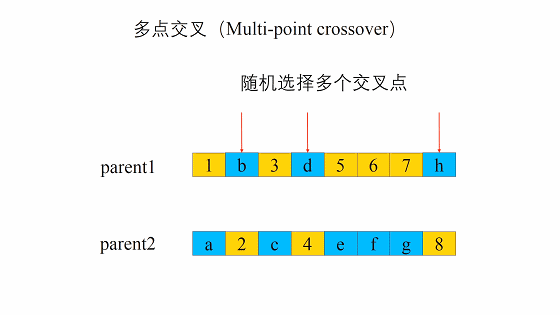
交叉
这个交叉过程和我们的生物其实很像,当然我们在我们的计算机里面对于数字我们可以将其转化为二进制,当做我们的DNA
变异
那这个在我们这里就更加简单了
我们只需要在交叉之后,再随机选择几个位置进行改变值就可以了。当然变异的概率是很小的,并且是随机的,这一点要注意。并且由于变异是随机的,所以不排除生成比原来还更加糟糕的个体。
选择
最后我们按照一定的规则去筛选这个些个体就可以了,然后淘汰原来的个体。那么在我们的计算机里面是使用了两个东西,首先我们要把原来二进制的玩意,给转化为我们原来的十进制然后带入我们的函数运算,然后保存起来,之后再每一轮统一筛选一下就好了。
代码编写
“开挂的API”
在开始编写我们的代码之前,我们必须要介绍几个API,这几个numpy的API简直就是开挂,同时也真是这几个API导致我们最难编写的部分变得相当简单。同时也正是这几个API导致不少人读不懂代码,因为代码没有解释,甚至在源码里面的解释也不清楚。
numpy.random.randint()
这个API的用法没有我先前说的那么简单。它的用法相当巧妙。
low: int
生成的数值最低要大于等于low。
(hign = None时,生成的数值要在[0, low)区间内)
high: int (可选)
如果使用这个值,则生成的数值在[low, high)区间。
size: int or tuple of ints(可选)
输出随机数的尺寸,比如size = (m * n k)则输出同规模即m * n k个随机数。默认是None的,仅仅返回满足要求的单一随机数。
dtype: dtype(可选):
想要输出的格式。如int64、int等等
输出:
out: int or ndarray of ints
返回一个随机数或随机数数组**
元素替换
这个其实主要是和numpy有关,这玩意支持布尔运算。
也就是这样。

所以如果我们想要交换我们两个arry数组的元素的话可以直接这样干
这里注意一下维度就行了


这样一来是不是直接完成了元素交换,也就是DNA交叉。
np.random.choice
这个也是开挂的玩意,我们先前说了我们要筛选也就是select。直接使用这个函数,就帮助我们搞定了。
首先是最基本的用法。
np.random.choice(5)#从[0, 5)中随机输出一个随机数
L = [1, 2, 3, 4, 5]#list列表
np.random.choice(L, 5)
>>>array([4, 3, 5, 3, 3])
L = [1, 2, 3, 4, 5]#list列表
np.random.choice(L, 5, replace=True)#可以看到有相同元素
权重
接下来就是我们的重点了

所以接下来怎么选择元素一目了然了吧。
当然我们这边其实选择的目的是去除不好的个体,那么其实就是选择好的个体。具体的看代码喽。
代码结构
好了废话了那么多,我们终于可以开始编码了。
这里其实也是分几块,就是我们前面的那几块。
完整代码
里面都有注释就不在说明了
import numpy as np
import matplotlib.pyplot as plt
Population_Size = 100
Iteration_Number = 200
Cross_Rate = 0.8
Mutation_Rate = 0.003
Dna_Size = 10
X_Range=[0,5]
def F(x):
'''
目标函数,需要被优化的函数
:param x:
:return:
'''
return np.sin(10 * x) * x + np.cos(2 * x) * x
def CrossOver(Parent,PopSpace):
'''
交叉DNA,我们直接在种群里面选择一个交配
然后就生出孩子了
:param parent:
:param PopSpace:
:return:
'''
if(np.random.rand()) < Cross_Rate:
cross_place = np.random.randint(0, 2, size=Dna_Size).astype(np.bool)
cross_one = np.random.randint(0, Population_Size, size=1) #选择一位男/女士交配
Parent[cross_place] = PopSpace[cross_one,cross_place]
return Parent
def Mutate(Child):
'''
变异
:param Child:
:return:
'''
for point in range(Dna_Size):
if np.random.rand() < Mutation_Rate:
Child[point] = 1 if Child[point] == 0 else 0
return Child
def TranslateDNA(PopSpace):
'''
把二进制转化为十进制方便计算
:param PopSpace:
:return:
'''
return PopSpace.dot(2 ** np.arange(Dna_Size)[::-1]) / float(2 ** Dna_Size - 1) * X_Range[1]
def Fitness(pred):
'''
这个其实是对我们得到的F(x)进行换算,其实就是选择的时候
的概率,我们需要处理负数,因为概率不能为负数呀
pred 这是一个二维矩阵
:param pred:
:return:
'''
return pred + 1e-3 - np.min(pred)
def Select(PopSpace,Fitness):
'''
选择
:param PopSpace:
:param Fitness:
:return:
'''
'''
这里注意的是,我们先按照权重去选择我们的优良个体,所以我们这里选择的时候允许重复的元素出现
之后我们就可以去掉这些重复的元素,这样才能实现保留良种去除劣种。100--》70(假设有30个重复)
如果不允许重复的话,那你相当于没有筛选
'''
Better_Ones = np.random.choice(np.arange(Population_Size), size=Population_Size, replace=True,
p=Fitness / Fitness.sum())
# np.unique(Better_Ones) #这个是我后面加的
return PopSpace[Better_Ones]
if __name__ == '__main__':
PopSpace = np.random.randint(2, size=(Population_Size, Dna_Size)) # initialize the PopSpace DNA
plt.ion()
x = np.linspace(X_Range, 200)
# plt.plot(x, F(x))
plt.xticks([0,10])
plt.yticks([0,10])
for _ in range(Iteration_Number):
F_values = F(TranslateDNA(PopSpace))
# something about plotting
if 'sca' in globals():
sca.remove()
sca = plt.scatter(TranslateDNA(PopSpace), F_values, s=200, lw=0, c='red', alpha=0.5)
plt.pause(0.05)
# GA part (evolution)
fitness = Fitness(F_values)
print("Most fitted DNA: ", PopSpace[np.argmax(fitness)])
PopSpace = Select(PopSpace, fitness)
PopSpace_copy = PopSpace.copy()
for parent in PopSpace:
child = CrossOver(parent, PopSpace_copy)
child = Mutate(child)
parent[:] = child
plt.ioff()
plt.show()
总结
遗传算法的优点:
- 与问题领域无关切快速随机的搜索能力。
- 搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较,robust.
- 搜索使用评价函数启发,过程简单
- 使用概率机制进行迭代,具有随机性。
- 具有可扩展性,容易与其他算法结合。
遗传算法的缺点:
遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码- 另外三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验.
- 没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢,要得要较精确的解需要较多的训练时间。
- 算法对初始种群的选择有一定的依赖性,能够结合一些启发算法进行改进。
- 算法的并行机制的潜在能力没有得到充分的利用,这也是当前遗传算法的一个研究热点方向。
在现在的工作中,遗传算法(1972年提出)已经不能很好的解决大规模计算量问题,它很容易陷入“早熟”。常用混合遗传算法,合作型协同进化算法等来替代,这些算法都是GA的衍生算法。
遗传算法具有良好的全局搜索能力,可以快速地将解空间中的全体解搜索出,而不会陷入局部最优解的快速下降陷阱;并且利用它的内在并行性,可以方便地进行分布式计算,加快求解速度。但是遗传算法的局部搜索能力较差,导致单纯的遗传算法比较费时,在进化后期搜索效率较低。在实际应用中,遗传算法容易产生早熟收敛的问题。采用何种选择方法既要使优良个体得以保留,又要维持群体的多样性,一直是遗传算法中较难解决的问题。
说人话就是
首先为了保证全局搜索性,这个收敛慢(没那么快找到点),为了提高速度,让这个算法跑快一点就容易跑太快(某一时刻富二代太多了都是富二代基因陷入局部最优)。也就是这个参数不好设置
你不注释,种群个数没变,在一定程度上有更多的可能变异。
你注释了,个数减少可能降低。当然100个不明显。
你可以试试,如果是100个个体结果是不一样的,但是相差不大,如果是10000个那结果都是一样的。
此外包括你的变异率,交换率都有影响。