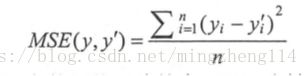tensorflow实战google深度学习框架阅读笔记——激活函数和损失函数篇
最近在阅读《tensorflow实战google深度学习框架》,对里面讲到的内容,重点部分做下摘抄和笔记,以备后面查阅。部分内容为本人个人理解,如果错误,请指正,如果侵权,请联系删除,谢谢。转载请注明出处,谢谢。
激活函数
概念,理解
在线性模型中,模型的输出为输入的线性加权和:
即 y=∑iwixi+b,而一个线性模型的最大特点就是任意线性模型的组合仍然还是线性模型,也就是说,它只可以用直线来划分数据
激活函数的作用,就是去线性化,原理:将每个神经元(也就是神经网络中的节点)的输出通过一个非线性函数,那么整个神经网络模型也就不再是线性的了,这个非线性函数就是激活函数。
高级用户也可以自己创建自己的激活函数,评价激活函数是否有用的主要因素参看如下几点:
1)该函数是单调的,随着输入的增加增加减小减小,从而利用梯度下降法找到局部极值点成为可能。
2)该函数是可微分的,以保证函数定义域内的任意一点上导数都存在,从而使得梯度下降法能够正常使用来自这类激活函数的输出。
下面介绍几个常用激活函数:
1.tf.nn.relu(features, name=None)
Computes rectified linear: max(features, 0).
· features: A Tensor. Must be one of the followingtypes: float32, float64, int32, int64,uint8, int16, int8.
· name: A name for the operation (optional).
注:
优点在于不受‘梯度消失’的影响,取值范围为[0,+∞]。
缺点在于当使用了较大的学习速率时,易受到饱和的神经元的影响。
2.tf.sigmoid(x, name=None)
Computes sigmoid of x element-wise.
Specifically, y = 1 / (1 + exp(-x)).
· x: A Tensor with type float, double, int32, complex64, int64, or qint32.
· name: A name for the operation (optional).
注:
优点在于sigmoid函数在样本训练的神经网络中可以将输出保持在[0.0,1.0]内部的能力非常有用。
缺点在于当输出接近饱和或剧烈变化时,对输出范围的这种缩减往往会带来一些不利影响。

3.tf.tanh(x, name=None)
Computes hyperbolic tangent of x element-wise.
· x: A Tensor with type float, double, int32, complex64, int64, or qint32.
· name: A name for the operation (optional).
注:
优点在于双曲正切函数和sigmoid函数比较相似,tanh拥有sigmoid的优点,用时tanh具有输出负值的能力,tanh的值域为[-1.0,1.0].
激活函数在tensorflow中的用法:
以Relu函数为例:
import tensorflow as tf
# 默认Tensorflow会话
sess = tf.InteractiveSession()
# Relu函数处理负数
print("anwser 1:",tf.nn.relu(-2.9).eval())
# Relu函数处理正数
print("anwser 2:",tf.nn.relu(3.4).eval())
# 产生一个4x4的矩阵,满足均值为0,标准差为1的正态分布
a = tf.Variable(tf.random_normal([4,4],mean=0.0, stddev=1.0))
# 对所有变量进行初始化,这里对a进行初始化
tf.global_variables_initializer().run()
# 输出原始的a的值
print("原始矩阵:\n",a.eval())
# 对a使用Relu函数进行激活处理,将结果保存到b中
b = tf.nn.relu(a)
# 输出处理后的a,即b的值
print("Relu函数激活后的矩阵:\n",b.eval())
结果如下:(由于不同的机器,运行结果会有不同)
anwser 1: 0.0
anwser 2: 3.4
原始矩阵:
[[-0.42271236 0.70626765 0.4220579 -1.19738662]
[-0.09090481 1.20085275 -1.37331688 -0.28922254]
[-0.63343877 0.04532439 -0.98322827 -0.01032094]
[0.364104 1.00423157 0.23247592 -1.13028443]]
Relu函数激活后的矩阵:
[[ 0. 0.70626765 0.4220579 0. ]
[0. 1.20085275 0. 0. ]
[0. 0.04532439 0. 0. ]
[0.364104 1.00423157 0.23247592 0. ]]
可以发现,对于输入是一个数字来说,输出满足公式。对于输入参数是一个矩阵的情况,relu函数对矩阵中的每一个数字均使用了Relu函数进行处理,负数直接变为0.0,正数保持不变。
其他的激活函数亦是如此。
损失函数
交叉熵
交叉熵刻画的是两个概率分布之间的距离,概率分布刻画了不同事件发生的概率,当事件总数总是有限的情况下,概率分布p(X = x)满足:
通过tensorflow实现交叉熵
通过tensorflow实现交叉熵,代码如下:
均方误差(MSE)
它的定义如下: