nn.LayerNorm的实现及原理
LayerNorm
在transformer中一般采用LayerNorm,LayerNorm也是归一化的一种方法,与BatchNorm不同的是它是对每单个batch进行的归一化,而batchnorm是对所有batch一起进行归一化的
y = x − E ( x ) V a r ( x ) + ϵ ∗ γ + β y = \frac{x-E(x)}{\sqrt{Var(x)+\epsilon}}*\gamma+\beta y=Var(x)+ϵx−E(x)∗γ+β
nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)
- normalized_shape:归一化的维度,int(最后一维)list(list里面的维度)
- eps:加在方差上的数字,避免分母为0
- elementwise_affine:bool,True的话会有一个默认的affine参数
elementwise_affine就是公式中的 γ \gamma γ和 β \beta β,前者开始为1,后者为0,二者均可学习随着训练过程而变化
举例
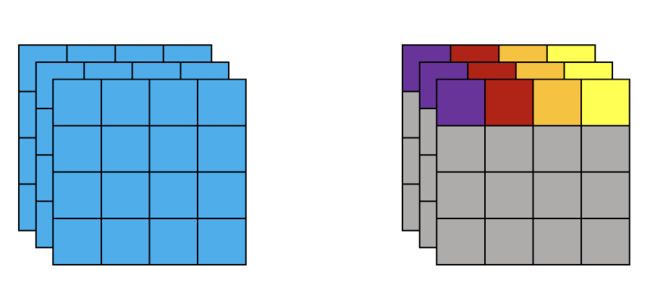
假设我们的输入为(1, 3, 5, 5)的变量,并对其进行LayerNorm,一般来说有两种归一化的方式。如下图所示,左边为第一种归一化方法,对所有channel所有像素计算;右边为第二种归一化方法,对所有channel的每个像素分别计算
- 计算一个batch中所有channel中所有参数的均值和方差,然后进行归一化,即(3, 5, 5)
- 计算一个batch中所有channel中的每一个参数的均值和方差进行归一化,即(3, 1, 1),计算25次
第一种
直接给出计算代码
注意:输入为(1, 3, 5, 5),layernorm的normalized_shape为[3, 5, 5],也就是说对后三维度进行归一化操作
from torch import nn
import numpy as np
import torch.nn as nn
from torchvision.transforms import Compose, ToTensor
import torch
def transform():
return Compose([
ToTensor(),
])
arr1 = np.arange(1,26).reshape(5, 5)
arr2 = np.arange(11, 36).reshape(5, 5)
arr3 = np.arange(31, 56).reshape(5, 5)
arr = np.dstack((arr1, arr2, arr3))
arr = np.reshape(arr,[5,5,3])
arr = arr.astype(np.float32)
# print(arr.shape) # [5, 5, 3]
arr = transform()(arr)
# print(arr.size()) # [3, 5, 5]
arr = arr.unsqueeze(0)
# print(arr.size()) # [1, 3, 5, 5]
''' 直接使用nn.LayerNorm函数计算 '''
norm = nn.LayerNorm([3, 5, 5])
print(norm(arr))
''' 手动计算 '''
u = arr.mean()
s = (arr-u).pow(2).mean()
x = (arr-u)/torch.sqrt(s+1e-5)
print(x)
'''
tensor([[[[-1.7584, -1.6890, -1.6196, -1.5502, -1.4808],
[-1.4114, -1.3420, -1.2725, -1.2031, -1.1337],
[-1.0643, -0.9949, -0.9255, -0.8561, -0.7867],
[-0.7173, -0.6478, -0.5784, -0.5090, -0.4396],
[-0.3702, -0.3008, -0.2314, -0.1620, -0.0925]],
...
[[ 0.3239, 0.3933, 0.4627, 0.5322, 0.6016],
[ 0.6710, 0.7404, 0.8098, 0.8792, 0.9486],
[ 1.0180, 1.0875, 1.1569, 1.2263, 1.2957],
[ 1.3651, 1.4345, 1.5039, 1.5733, 1.6427],
[ 1.7122, 1.7816, 1.8510, 1.9204, 1.9898]]]],
grad_fn=)
tensor([[[[-1.7584, -1.6890, -1.6196, -1.5502, -1.4808],
[-1.4114, -1.3420, -1.2725, -1.2031, -1.1337],
[-1.0643, -0.9949, -0.9255, -0.8561, -0.7867],
[-0.7173, -0.6478, -0.5784, -0.5090, -0.4396],
[-0.3702, -0.3008, -0.2314, -0.1620, -0.0925]],
...
[[ 0.3239, 0.3933, 0.4627, 0.5322, 0.6016],
[ 0.6710, 0.7404, 0.8098, 0.8792, 0.9486],
[ 1.0180, 1.0875, 1.1569, 1.2263, 1.2957],
[ 1.3651, 1.4345, 1.5039, 1.5733, 1.6427],
[ 1.7122, 1.7816, 1.8510, 1.9204, 1.9898]]]])
'''
第二种
直接给出计算代码
注意:我们的输入是(1, 3, 5, 5),如果要完成第二种方法,我们layernorm只需要提供一个参数,即norm = nn.LayerNorm(3),但是如果只提供一个参数,默认为对最后一维进行归一化,所以我们需要将输入进行变化,即变为(1, 5, 5, 3)。
特别的在transformer中我们的数据维度一般在最后一维,也就是(1, 5, 5, 3)的形式,所以可以直接用layernorm函数进行归一化,如果是普通的卷积层,形式为(1, 3, 5, 5)需要手动实现,下面分别实现了这两种方法
from torch import nn
import numpy as np
import torch.nn as nn
from torchvision.transforms import Compose, ToTensor
import torch
def transform():
return Compose([
ToTensor(),
])
''' 数据初始化 '''
arr1 = np.arange(1,26).reshape(5, 5)
arr2 = np.arange(11, 36).reshape(5, 5)
arr3 = np.arange(31, 56).reshape(5, 5)
arr = np.dstack((arr1, arr2, arr3))
arr = np.reshape(arr,[5,5,3])
arr = arr.astype(np.float32)
arr = transform()(arr)
arr = arr.unsqueeze(0) # [1, 3, 5, 5]
''' [1, 3, 5, 5] -> [1, 5, 5, 3] '''
arr = arr.permute(0, 2, 3, 1).contiguous()
print(arr.size()) # [1, 5, 5, 3]
''' LayerNorm函数计算 '''
norm = nn.LayerNorm(3)
print(norm(arr))
''' [1, 5, 5, 3] -> [1, 3, 5, 5] '''
arr = arr.permute(0, 3, 1, 2)
print(arr.size()) # [1, 3, 5, 5]
''' 手动计算 '''
# 1. 归一化
u = arr.mean(dim=1, keepdim=True) # mean # [1, 1, 5, 5]
s = (arr - u).pow(2) # sigma^2 # [1, 3, 5, 5]
s = s.mean(1, keepdim=True) # [1, 1, 5, 5]
x = (arr - u) / torch.sqrt(s + 1e-6) # layer norm
print(x)
# 2. 加上affine
weight = nn.Parameter(torch.ones(3)) # [1, 3]
bias = nn.Parameter(torch.zeros(3))
print(weight)
print(weight[:, None, None], weight[:, None, None].size()) # [3, 1, 1]
x = weight[:, None, None]*x + bias[:, None, None]
'''
torch.Size([1, 5, 5, 3])
tensor([[[[-1.0690, -0.2673, 1.3363],
[-1.0690, -0.2673, 1.3363],
[-1.0690, -0.2673, 1.3363],
[-1.0690, -0.2673, 1.3363],
[-1.0690, -0.2673, 1.3363]],
...
[[-1.0690, -0.2673, 1.3363],
[-1.0690, -0.2673, 1.3363],
[-1.0690, -0.2673, 1.3363],
[-1.0690, -0.2673, 1.3363],
[-1.0690, -0.2673, 1.3363]]]], grad_fn=)
torch.Size([1, 3, 5, 5])
tensor([[[[-1.0690, -1.0690, -1.0690, -1.0690, -1.0690],
[-1.0690, -1.0690, -1.0690, -1.0690, -1.0690],
[-1.0690, -1.0690, -1.0690, -1.0690, -1.0690],
[-1.0690, -1.0690, -1.0690, -1.0690, -1.0690],
[-1.0690, -1.0690, -1.0690, -1.0690, -1.0690]],
...
[[ 1.3363, 1.3363, 1.3363, 1.3363, 1.3363],
[ 1.3363, 1.3363, 1.3363, 1.3363, 1.3363],
[ 1.3363, 1.3363, 1.3363, 1.3363, 1.3363],
[ 1.3363, 1.3363, 1.3363, 1.3363, 1.3363],
[ 1.3363, 1.3363, 1.3363, 1.3363, 1.3363]]]])
'''