玩谁是卧底吗?用C语言帮你盘逻辑
前言
读完这篇博客你可以收获什么?
①巧妙的递归。
②磨炼逻辑推导能力。
③锻炼将人脑思考过程转化为计算机语言的能力。
④如何在时间复杂度为 O(n!) 内生成下排列组合数。
话不多说说,侦探们我们这就开始推理。️♂️
作者概况: 就读南京邮电大学努力学习的大一小伙
联系方式:2879377052(QQ小号)
资源推荐:C语言从入门到进阶
今日书籍分享: 《深入理解计算机系统》 三十天有效
目录
案件一:谁是凶手?
案件二:谁打碎了花瓶
案件三:确定比赛名次
四、后记
案件一:谁是凶手?
日本某地发生了一件谋杀案,警察通过排查确定杀人凶手必为4个嫌疑犯的一个。
以下为4个嫌疑犯的供词:
A说:不是我。
B说:是C。
C说:是D。
D说:C在胡说
已知3个人说了真话,1个人说的是假话。
现在请根据这些信息,写一个程序来确定到底谁是凶手。
【思路】
①对于计算机而言,最好的推理办法就是枚举法,因为只要答案唯一,我们就一定可以得出真相。 所以我们要做的就是枚举所有的情况。
②再判断所枚举的情况是否满足三个人说真话,三个人说假话的条件
③我们怎么实现判断说真话的数量呢?很简单,根据逻辑判断符,为真则表达式的值为1,为假表达式的值为0,所以我们只要使得最终各个表达式的值相加为3即可得出真相。
【办案】
int main()
{
char killer;
for (killer = 'A'; killer <= 'D'; killer++)
{
int cnt = 0;
if (killer != 'A')
cnt++;
if (killer == 'C')
cnt++;
if (killer == 'D')
cnt++;
if (killer != 'D')
cnt++;
if (cnt == 3)
{
printf("killer = %c", killer);
break;
}
}
return 0;
}【破案了】
案件二:谁打碎了花瓶
家里有A,B,C,D四个孩子,其中一个孩子把花瓶打碎了。
A说:我没有打破花瓶。
B说:是我打破的。
C说:不是A打破的。
D说:不是B打破的。
已知,打破花瓶的孩子一定在撒谎,但是其他人不确定。那么,是谁打破了花瓶?
【思路】同案件二的分析,基本思路是枚举法,所给的条件是打破花瓶的孩子一定在撒谎。但这题其实还有点小技巧,因为没打破花瓶的人说的话可真可假,所以他们说的话本身没有意义。
【办案】
int main()
{
char killer = 0;
for (killer = 'A'; killer <= 'D'; killer++)
{
int ans[4] = { 1,1,1,1 };//默认都说真话
ans[killer - 'A'] = 0;//凶手说假话
switch (killer)
{
case 'A':
if (ans[killer - 'A'] == (killer != 'A'))//相等说明没有矛盾,根据答案唯一可知谁是凶手
{
printf("killer = %c", killer);
goto over;
}
break;
case 'B':
if (ans[killer - 'A'] == (killer == 'B'))
{
printf("killer = %c", killer);
goto over;
}
break;
case 'C':
if (ans[killer - 'A'] == (killer != 'A'))
{
printf("killer = %c", killer);
goto over;
}
break;
case 'D':
if (ans[killer - 'A'] == (killer != 'B'))
{
printf("killer = %c", killer);
goto over;
}
break;
}
}
over:
return 0;
}【破案了】
案件三:确定比赛名次
前两道案件都是开胃菜,用脑子空想都能想出来。但下面这个案件就要复杂的多了
5位运动员参加了10米台跳水比赛,有人让他们预测比赛结果:
A选手说:B第二,我第三;
B选手说:我第二,E第四;
C选手说:我第一,D第二;
D选手说:C最后,我第三;
E选手说:我第四,A第一;
比赛结束后,每位选手都说对了一半,请编程确定比赛的名次。
【思路】虽然题目复杂了很多,但我们依然可以延续案件一的枚举思想:管他这么多,枚举就完事了。只要能保证条件——只说对一般即可。
【注意点】枚举过程中需要注意的一个问题是,名次不能重复,所以在每次枚举的时候我们首先要保证名次没有重复,否则continue。
【办案】
int main()
{
int f[6] = {0};
int a = 0, b = 0, c = 0, d = 0, e = 0;
for (a = 1; a <= 5; a++)
{
f[a] = 1;
for (b = 1; b <= 5; b++)
{
if (f[b])
continue;
f[b] = 1;
for (c = 1; c <= 5; c++)
{
if (f[c])
continue;
f[c] = 1;
for(d = 1; d <= 5; d++)
{
if (f[d])
continue;
f[d] = 1;
for (e = 1; e <= 5; e++)
{
if (f[e])
continue;
if ((b == 2) + (a == 3) == 1 && //B第二,我第三
(b == 2) + (e == 4) == 1 && //我第二,E第四
(c == 1) + (d == 2) == 1 && //我第一,D第二
(c == 5) + (d == 3) == 1 && //C最后,我第三
(e == 4) + (a == 1) == 1) //我第四,A第一
{
printf("a = %d, b = %d, c = %d, d = %d, e= %d",a,b,c,d,e);
goto over;//跳出多重循环用goto最好
}
f[e] = 0;
break;
}
f[d] = 0;
}
f[c] = 0;
}
f[b] = 0;
}
f[a] = 0;
}
over:
return 0;
}
【破案了】
案子虽然是结了,但上面的代码写的也太矬了,怎么能体现出优秀程序员的深厚功底呢?我们来试着改进一下。
【改进①】
上面判断是否重复的过程实际是哈希表思想的运用,即数组下标与元素一一映射,不太会,看看这篇博客【跟着英雄学算法第⑤天】计数法——附Leetcode刷题题解(C语言实现)。
但是,我们注意到判断是否重复只有两种情况,用01即可一反映,没必要用一个数组去存储。因此我们可以联想二进制,用一个数的二进制某一位为0还是1反映是否重复。这里运用到哈希中的位图。将原来需要一个数组的空间压缩到只需要一个int即可。
(我们这里封装一个函数来实现,每次判断时调用函数即可)
int check_data(int*p)
{
int tmp = 0;
for (int i = 0; i < 5; i++)
{
tmp |= 1 << (p[i] - 1);
}
return tmp == 0B11111;
//tmp每次或上一位1,p[i]如果是1~5都有,则1<<1到1<<5都或上的结果将会是00111110,如果有并列,则一定会至少却其中一个1,结果就不会是00111110,所以可以判断tmp最终的结果是不是这个数字来判断有没有重复。
}
【改进②】
上面循环的代码看起来很冗长,但其实本质上有很多的代码都是重复的,因此我们可以使用递归思想来减少代码。
int check_data(int*p)
{
int tmp = 0;
for (int i = 0; i < 5; i++)
{
tmp |= 1 << (p[i] - 1);
}
return tmp == 0B11111;
}
void diveRank(int* p, int n)
{
if (n >= 5)
{
if (!check_data(p))
return;
if ((p[1] == 2) + (p[0] == 3) == 1 &&
(p[1] == 2) + (p[4] == 4) == 1 &&
(p[2] == 1) + (p[3] == 2) == 1 &&
(p[2] == 5) + (p[3] == 3) == 1 &&
(p[4] == 4) + (p[0] == 1) == 1)
{
for (int i = 0; i < 5; i++)
{
printf("%d ", p[i]);
}
putchar('\n');
}
return;
}
for (p[n] = 1; p[n] <= 5; p[n]++)
{
diveRank(p,n + 1);
}
}
int main()
{
int p[5] = {0};
diveRank(p, 0);
return 0;
}【理解】
递归时一层一层理解。首先生成p[0],p[0]有1~5五种取法,对于每一种取法p[1]也有5种取法,依次类推,实现【办案】中的循环效果。
【究极改进】
递归虽然使得代码行数看起来更少,但是时间复杂度仍然是O(n^n),那如何降低到O(n!)呢?我们可以进一步优化遍历方式,每次直接生成1~5的全排列数
先上代码,可能有点难理解。
void swapArgs(int* a, int* b) //交换函数
{
int tmp;
tmp = *a;
*a = *b;
*b = tmp;
}
void diveRank(int* p, int n)
{
if (n >= 5) //此时的n也是用来控制循环层数的。
{
if ((p[1] == 2) + (p[0] == 3) == 1 && //B第二,我第三
(p[1] == 2) + (p[4] == 4) == 1 && //我第二,E第四
(p[2] == 1) + (p[3] == 2) == 1 && //我第一,D第二
(p[2] == 5) + (p[3] == 3) == 1 && //C最后,我第三
(p[4] == 4) + (p[0] == 1) == 1) //我第四,A第一
//由于此时是执行的全排列,所以查重也省了。
{
for (int i = 0; i < 5; i++)
{
printf("%d ", p[i]);
}
putchar('\n');
}
return;
}
int i;
for (i = n; i < 5; i++) //这个递归方式就完成了对1~5的全排列,方法是从后向前不停的执行交换。可以参考改进二和原代码,将这个递归程序写回成循环后,可以更好的理解。
{
swapArgs(p + i, p + n);
diveRank(p, n + 1);
swapArgs(p + i, p + n);
}
}
int main()
{
int p[5] = { 1, 2, 3, 4, 5 }; //当然由于是全排列,所以初值必须给好。
diveRank(p, 0);
return 0;
}【理解】
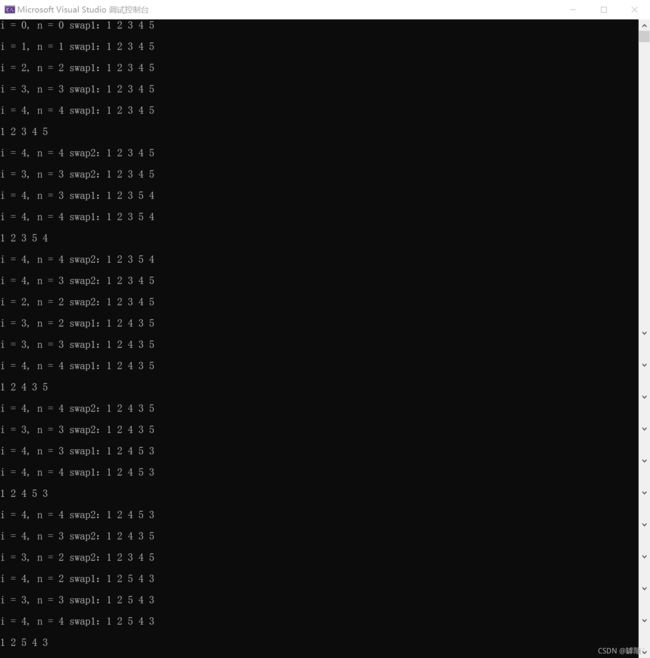
在核心代码处我分别打印交换时的i,n的值,第一次交换后第二次的序列,以及每次 n >= 5时进入判断语句参与判断的序列。
【分析】
我们首先来分析如何生成组合数。
给我们两个数字1 2,显然组合只有两种情况 :1 2 和 2 1;
给我们三个数字1 2 3,显然组合有六种情况:1 2 3 ,1 3 2,2 1 3,2 3 1, 3 1 2, 3 2 1
给我们四个数字1 2 3 4,组合情况怎么看呢:
当我们确定第一个数字为1 ,后面三个数字的排列方式不是和 1 2 3模式相同吗,依次类推,就产生了我们的递推思想。
在这里n控制着循环的层数。
(1)从n = 0到n = 4,我们一口气进入了第五层循环,由于 i = n = 4 相当于给我们五个数字,确定前四个数字,排列的方式显然是惟一的为1 2 3 4 5。
(2)当从第四层循环回到第三层循环时,i = n = 3,,相当于先确定前面三个数字,那么 4 5互换产生了新的排列方式
(3)最后分析第三层循环回到第二层循环时,i = n = 2,相当于确定前面的两个数字,那么 3 4 5之间是可以互换的。而3 4 5之间的互换与(2)中的互换方式是一致的
相信讲到这里大家理解了互换的模式。
【问】为什么要执行这两条效果相反的语句呢?
【答】每次从循环中出来时排列都会被还原为 1 2 3 4 5,这样就不会对下一次的递归产生影响,所以说每一次的序列肯定都是独一无二的,因为都是从一个炉子里以不同的方式捏出来的。
四、后记
有同学肯定会说,写完这段代码游戏早就结束了,你这么一说,好像是诶,但学习到知识才是我们的初心(强行解释),难道不是吗?