算法设计技巧: 深度优先搜索(DFS)

前文介绍了用广度优先搜索(Breadth-First-Search)的方法遍历一个图$G=(V,E)$. 本文介绍另一种常用的方法: 深度优先搜索(Depth-First-Search). DFS与BFS相比, 它的主要特点是遍历顶点的顺序满足一定的规律, 利用这些规律可以对顶点和边进行分类, 从而应用与其它问题的求解(例如计算拓扑排序和强连同分支, 参考下文).

深度优先搜索

给定图$G=(V,E)$和初始点$u\in V$. 从$u$开始递归地搜索与$u$邻接的(且未被搜索的)顶点$v$. 伪代码如下：

DFS(G, u):
    label u as discovered
    for each v that is adjacent to u 
        if v is not discovered then
            DFS(G, v)

DFS除了遍历所有顶点, 我们对其搜索过程有如下观察:

1. 记录顶点的访问顺序得到有向的搜索树.

• 初始时间为0, 所有顶点标记为白色
• 发现时间: 顶点$u$被发现的时间(标记为灰色）
• 结束时间: 顶点$u$及其所有邻接点$v$被发现的时间 (标记为黑色)

考虑$(u,v)\in E$, 如果$u$的发现时间早于$v$的发现时间, 则$u$是$v$的父节点. 如下图所示, $d[u],f[u]$分别代表发现时间和结束时间.

2. DFS对边进行分类.

根据(有向)搜索树, 我们把边分成如下几类:

• 树边(Tree Edge): DFS得到的搜索森林 (蓝色)
• 前向边(Forward Edge): 搜索树中祖先节点指向后继节点的边 (绿色)
• 反向边(Backward Edge): 搜索树中后继节点指向祖先节点的边 (红色)
• 交叉边(Cross Edge): 用$(u,v)$代表它, 那么$u,v$没有前后继关系, 或$u,v$在不同的搜索树中 (灰色)
  

Python实现

class DFS(object):
    """ Depth First Search
    """

    def __init__(self, G):
        """
        :param G: Graph, 数据结构为邻接表:
            key = node index, value = list of adjacent node indices, e.g.,
        {
            0: [...]  # node 0
            1: [...]  # node 1
            ...
        }
        """
        self._G = G
        # colors
        # white-未被发现
        # gray-发现但未发现它所有邻接点
        # black-发现它以及所有的邻接点
        self._c = {v: 'white' for v in self._G.keys()}
        self._time = 0
        # discovering time
        self._d = {v: 0 for v in self._G.keys()}
        # finishing time
        self._f = {v: 0 for v in self._G.keys()}
        # 记录搜索森林
        # list of dict: key = node, value = parent
        self._forest = []

    def _traverse(self, u, p):
        """ DFS.
        :param u: 搜索的初始顶点编号, int
        :param p: 用来记录搜索树, dict, key = node, value = parent
        注意: 如果搜索树只是一个孤立点, 结果不会保存在p中.
        """
        self._time += 1
        self._c[u] = 'gray'  # 发现u, 标记为灰色
        self._d[u] = self._time  # 记录发现时间
        for v in self._G[u]:  # 考虑所有(u,v)
            if self._c[v] == 'white':
                p[v] = u
                self._traverse(v, p)
        self._time += 1
        self._c[u] = 'black'  # 结束u, 标记为黑色
        self._f[u] = self._time  # 记录结束时间
        # 孤立点
        if not p:
            p[u] = None

    def run(self, vertices=None):
        """
        :param vertices: list, 按照列表中顶点的顺序执行DFS.
        """
        if not vertices:
            vertices = self._G.keys()
        for u in vertices:
            p = {}
            if self._c[u] == 'white':
                self._traverse(u, p)
            if p:
                self._forest.append(p)
        return self

完整代码

拓扑排序

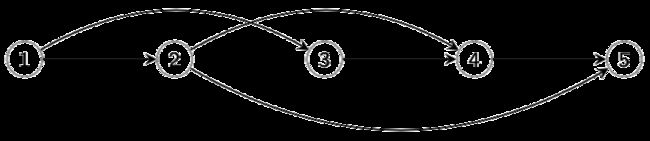
给定一个有向无环图$G=(V,A)$, 其中$V$代表顶点的集合, $A$代表有向边(Arc)的集合. 我们要对顶点进行拓扑排序(Topological Sort), 即找到映射$\pi :V\to \{1,2,\dots ,|V|\}$, 使得$\forall (u,v)\in A$, 我们有$\pi (u)<\pi (v)$. 换句话说, 我们对顶点进行编号, 使得所有的边是从左到右的(如下图所示).

算法思路

用DFS遍历$G$并记录每个顶点的完成时间, 按完成时间的先后对顶点从大到小编号.

正确性¹

用DFS对有向无环图的边进行分类, 用反证法证明两点(省略):

1. 单个搜索树中无反向边.
2. 搜索树之间无反向边.

Python实现

from dfs import DFS  # 引用前面写好的DFS类


class TopologicalSort(object):
    """ Apply depth-first-search to topological sort.
    """

    def __init__(self, G):
        """
        :param G: Graph, 数据结构为邻接表:
            key = node index, value = list of adjacent node indices, e.g.,
        {
            0: [...]  # node 0
            1: [...]  # node 1
            ...
        }
        """
        self._G = G
        self._G1 = {}  # 拓扑排序结果

    def run(self):
        d = DFS(self._G).run()
        f = d.get_finishing_times()
        # 把顶点按finishing time排序(降序)
        items_sorted = list(sorted(f.items(), key=lambda x: x[1], reverse=True))
        # 顶点到编号的映射
        m = {items_sorted[i][0]: i for i in range(len(items_sorted))}
        # 拓扑排序
        for u, edges in self._G.items():
            self._G1[m[u]] = [m[v] for v in edges]
        return self

完整代码

强连通分支

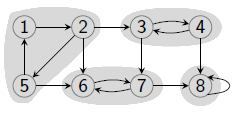
给定一个图$G=(V,E)$和集合$C\subseteq V$. 称$C$是一个 强连通分支(Strongly Connected Component) 当$C$是中任意两点连通且$C$的元素个数最大(Maximal). (注意: 这里Maximal指的是不存在更大的集合$C^{\prime }\supset C$满足$C^{\prime }$中任意两点连通.)

算法

1. 对$G$执行DFS. 按结束时间(Finishing Time)从大到小对顶点排序.
2. 把$G$中的边反向得到它的转置图$G^T$, 按照第一步得到的顶点顺序对$G^T$执行DFS.

正确性¹

1. $G^T$和$G$的强连通分支是相同的. 分别对$G$和$G^T$执行DFS后得到的搜索森林保证了每棵树的顶点之间是连通的.
2. 证明每个连通的顶点集合是Maximal(证明略).

from dfs import DFS  # 引用前面写好的DFS类


class SCC(object):
    """
    Compute strongly connected components (SCC).
    """

    def __init__(self, G):
        """
        :param G: Graph, 数据结构为邻接表:
            key = node index, value = list of adjacent node indices, e.g.,
        {
            0: [...]  # node 0
            1: [...]  # node 1
            ...
        }
        """
        self._G = G
        self._scc = None  # 计算结果

    @staticmethod
    def _transpose(G):
        """ 计算G的转置(Transpose graph)
        """
        G_t = {v: [] for v in G.keys()}
        for u, edges in G.items():
            for v in edges:
                G_t[v].append(u)
        return G_t

    def run(self):
        # step1: Apply DFS to G
        d1 = DFS(self._G).run()
        f = d1.get_finishing_times()
        # 把顶点按finishing time排序(降序)
        items_sorted = sorted(f.items(), key=lambda x: x[1], reverse=True)
        # step2: Apply DFS to the transpose of G
        vertices = [item[0] for item in items_sorted]
        d2 = DFS(self._transpose(self._G)).run(vertices)
        # format result
        forest = d2.get_search_forest()
        self._scc = self._format_scc(forest)
        return self

    @staticmethod
    def _format_scc(forest):
    	""" 计算搜索森林中每颗树的顶点集合
    	"""
        scc = []
        for tree in forest:
            tree_vertices = set({})
            for k, v in tree.items():
                tree_vertices.add(k)
                if v:
                    tree_vertices.add(v)
            scc.append(tree_vertices)

        return scc

完整代码

参考文献

---

1. T.H. Cormen, C. E. Leiserson, R.L. Rivest and C. Stein. Introduction to Algorithms. Third edition. The MIT Press, 2009. ↩︎ ↩︎