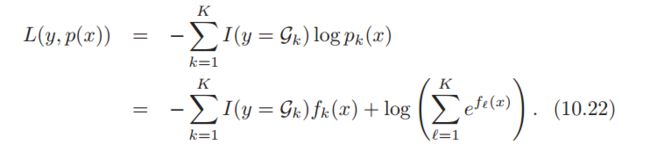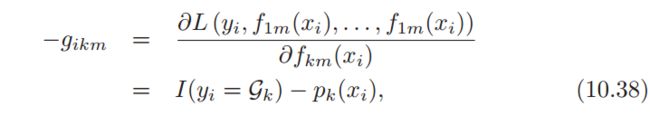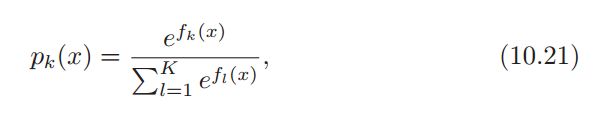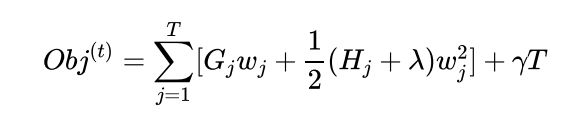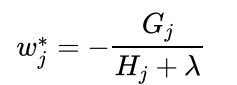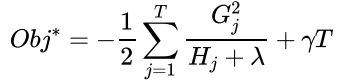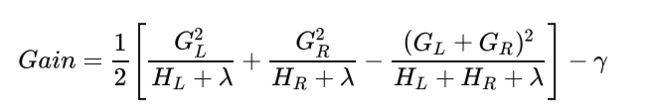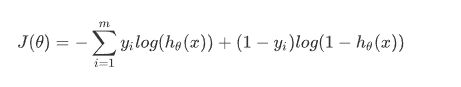Q
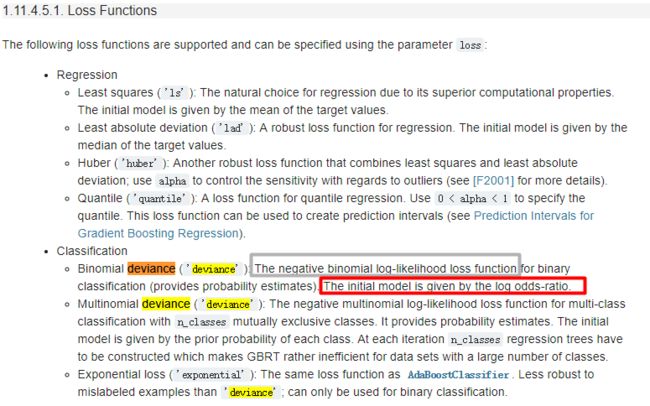
GBDT是一种基于前向策略的加法模型, 每阶段使用一个基模型去拟合上一阶段基模型的残差. 残差是连续值, 因此用到的是回归树. 为什么当GBDT用作分类任务时可以选择deviance loss和exponential loss, 而这两个损失函数的$y^{(i)}$取值都为0-1标量, 如何计算残差?
A
在梯度提升做二分类任务时, $y^{(i)}$不再是标量, 而是概率(为正的概率); 另一方面, deviance loss(二分类就是交叉熵损失)和exponential loss都是评价预测(概率)与真实(概率)之间的差距, 也就是残差, 是一个连续值, 从而是一个回归问题.
GBDT如何做分类任务?
若选择deviance loss为分类任务的损失函数:
求损失函数对当前模型的负梯度:
作为残差的近似(就是梯度下降求解Logistics回归参数的式子, 就是残差, 惊人的联系)
其中概率$p_k(x)$的计算:
- 概率来自$f_k(x)$, 也就是叶节点的输出(输出为对数几率, 后转换为概率), 其中$f_k(x) \geq 0$, $\sum_{k=1}^{K} p_k(x) = 1$
也就是说, GBDT做分类任务时, 提升的是关于概率的近似残差
决策树的两个参数
损失函数的负梯度仅仅是用来作为
目标(残差的近似)使用
最小二乘法计算树结构(决策树参数一)-
使用
目标(残差的近似)计算叶子节点权值(决策树参数二)(这里可以和XGBoost进行比较, XGBoost使用最小化损失函数计算树结构, 使用二阶梯度作为残差的近似)
再看梯度提升算法
注意:
- 在训练过程中并不是求的与上一棵树结果的残差, 而是求的与前面所有树和的残差! 在预测过程中, 可分别计算每棵树, 求和即为最后的结果
- 在做分类任务时, 当树构建完成后
- 计算每个叶节点的权值(这里的权值是对数几率)
- 把对数几率转换为概率值(二分类就是logistics函数, 多分类用上面的概率公式)
- 得到提升的概率值
- 对与(c)计算叶权重时, 使用均方误差就是均值, 其他函数需要带入计算最优权值
GBDT与XGBoost在算法上的比较
XGBoost的每一阶段的损失函数(经验损失 + 结构损失):
其中, $w$是叶节点权值, 也是模型需要提升的值, 相当于GBDT中损失函数的负梯度:
- 叶节点权值是如何得来的? 使用牛顿法计算的增量$\Delta \theta = -\frac{G}{H}$作为梯度值的近似
- 这里用到了二阶导信息, 更加接近于真实值, 所以收敛速度更快
- 分母加上了对结构损失的惩罚(如果结构复杂, 就少下降一点, 降低影响)
每个叶子是相互独立的, 因此可以直接带入到损失函数中:
GBDT的损失函数仅用在了计算目标值(进而计算叶节点的值), 而XGBoost不仅仅是计算叶节点的值, 进一步把损失函数用在了计算树结构:
- 选择划分后损失降低最多的特征作为分裂特征
- 为什么GBDT不这么做呢? 可能是直接使用的CART的原因吧!
- 为什么XGBoost要这么做呢? $G, H$都求出来了, 又不和叶子节点相关, 很完美呀!(XGBoost完全基于$G, H$求解)
- 求每个样本的近似残差(一阶梯度 vs 二阶梯度)
- 计算树结构(最小二乘法 vs 损失函数)
- 计算叶子权值(落在叶子节点上的样本取平均)
GBDT与XGBoost算法上区别的总结
-
GBDT使用一阶梯度作为残差的近似, XGBoost使用二阶梯度作为残差的近似
- 更加接近真实值, 收敛更快
GBDT的损失函数没有考虑到树的复杂度, 而XGBoost添加了正则项对复杂度进行了惩罚
-
GBDT是用的最小二乘法计算树结构(CART), 而XGBoost使用的是损失函数来计算树的结构
(注: 这里的区别仅仅是算法上的, XGBoost在并行上, 过拟合上, 适用范围上还有改进)
另外, XGBoost的剪枝是基于最小增益Gamma的. 需要注意的是, 预剪枝的效果没有后剪枝好(容易出现下潜不足), 因此XGBoost选择了同一层所有节点都做分裂, 后剪枝的方法.
XGBoost: Introduction to Boosted Trees
GBDT vs 离散特征(Categorical Features)
- GBDT在处理离散特征时, 会默认特征是有序的
- 如果排序后的特征对应的标记为为[0, 1, ..., 0, 1]交叉型, 则不能很好的分类
- 如果使用one-hot, 对于高基数离散特征, 会生成不平衡的树, 且每次划分带来的增益较少
- 解决办法: 计算每个特征取值的熵, 通过熵的大小对特征进行有序重编码
- LightGBM vs 离散特征
- 根据标签的关联性对特征进行重排序, 特别的, 使用加速值(
sum_gradient / sum_hessian)度量标签与特征取值的关联性 - catboost同样是把离散值转化为连续值来处理类别特征
- 根据标签的关联性对特征进行重排序, 特别的, 使用加速值(
LightGBM: Optimal Split for Categorical Features
LightGBM: Categorical feature support
GBDT vs LR vs DNN
GBDT损失函数的负梯度作为残差的近似 与 LR求损失函数的负梯度去更新参数是一个性质吗?
对于logloss:
$$
J(\theta) = - \sum_{i=1}^{m} y_i log(h_{\theta}(x)) + (1 - y_i)log(1 - h_{\theta}(x))
$$
不同在于GBDT的变量为模型$h_{\theta}(x)$
- 对$h_{\theta}(x)$求偏导, 来作为残差的近似. ($h_{\theta}(x)$虽然为一个函数, 但在这里视为为变量)
而LR的变量进一步为每个参数$\theta_j$
- 对$\theta_j$求偏导. (因此$\theta_j$需要归一化, 这个过程是通过对特征的归一化实现的)
总结
GBDT 和 梯度下降的LR 都可以认作是在拟合残差(一步一步向目标值的迭代迈进), 不同在于一个是对模型求导, 作为的残差的近似(其实也是提升模型的一个方向). 一个是对参数求导, 作为提升模型的方向. 同样, DNN也可以这么想, 每一次更新参数为了更接近目标.
一个把梯度作为拟合的目标, 一个使用梯度下降来更新参数
logloss vs cross entropy
logloss 用来评价预测结果为概率的分类器的性能
cross entropy 是损失函数, 衡量的是样本的不确定性
其实就是一样的(ps: wikipedia会把logloss指向cross entropy)
Quora: What is an intuitive explanation for the log loss function?
Wikipedia: cross entropy
附录1: GBDT分类任务源码解析
sklearn GBDT 文档
在每个阶段, 使用回归树去拟合
交叉熵损失的负梯度
http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html
另外的一个文档
- 使用的是负的对数似然函数作为损失
- 使用对数几率初始化模型(叶节点的值为对数几率)
- 需要注意的一点, 使用deviance输出的是
概率, 所以有可能评价的是概率上的损失
http://scikit-learn.org/stable/modules/ensemble.html#classification
查看源代码
- 确实是拟合的交叉熵损失的负梯度
- 基模型使用的回归树!
其中的残差的计算
numpy.ravel(): 把多维数组转换为一维数组(两个类别连接起来)
scipy.expit(): logistic function, expit(x) = 1/(1+exp(-x)), logistic 变换, 把对数几率转为概率
负梯度的值(残差的近似)就是残差(使用梯度下降求解的Logistic回归相同)
https://github.com/scikit-learn/scikit-learn/blob/a24c8b46/sklearn/ensemble/gradient_boosting.py#L1225
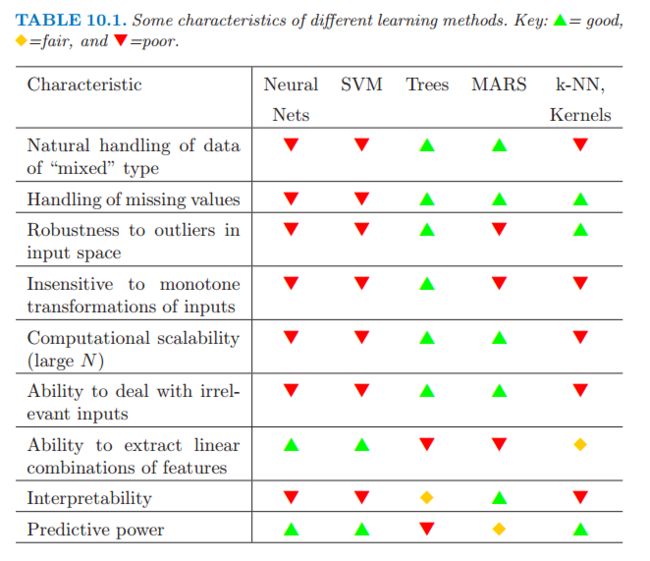
附录2: 树模型与其他模型的比较
- 树模型是不能提取特征的线性组合信息的
- SVM的好处就是就是泛化能力强和能处理特征间的线性组合问题
其他参考:
The Elements of Statistical Learning
Scikit Binomial Deviance Loss Function