dp第三弹~数位统计类dp，状压dp，树形dp

计数dp

dp最难的就是想出来状态表示和分情况讨论

计数问题
类似小学数奥问题，最重要的就是分情况讨论

我们这里首先实现一个count(n， x)函数，这个函数的作用就是，求出来1到n中x出现的次数，一般x是0~9
对于本题，答案就是count（b， x）- count（a-1， x）

举个例子，1~n， x = 1
然后有abcdefg七位，求出来1在每一位上出现的次数，然后累加就是总次数
解释一下上图
1 <= abc1efg <= abcdefg
分成两种情况，
一种是abc任取 000~abc-1 这时候efg可任取，由于一直d是x（这里就是1） 然后这时候数量就是abc*1000：理解为abc种，每一种有1000种
第二种就是abc就 等于abc，这时候再次细分成三种情况，
1.一种是d < x(这里为1) 这时候，显然不可能存在可取的情况
2.d ==x， 这时候efg可取000~efg 一共efg+1种
3.d > x 这时候efg可任取000~999共1000种情况

然后将两种情况数相加就OK了
边界情况：
 当1出现在最高位的时候，第一种情况不存在
 当枚举0的时候，第一种情况就变成了1~abc-1因为数字不能有前导0
 

#include 
#include 
#include 

using namespace std;

const int N = 10;

/*

001~abc-1, 999

abc
    1. num[i] < x, 0
    2. num[i] == x, 0~efg
    3. num[i] > x, 0~999

*/

int get(vector<int> num, int l, int r)//这个函数是用来求第一种情况的 
{
/*
就是求一下数，也就是样例中第一种情况的abc，或者之后 i==x的情况，求一下后边的数 
*/
    int res = 0;
    for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
    return res;
}

int power10(int x)//求一下10的i次方 
{
    int res = 1;
    while (x -- ) res *= 10;
    return res;
}

int count(int n, int x)
{
    if (!n) return 0;

    vector<int> num;
    while (n)
    {
        num.push_back(n % 10);
        n /= 10;
    }
    n = num.size();

    int res = 0;
    for (int i = n - 1 - !x; i >= 0; i -- )//从最高位开始枚举，因为用到了vector，所以从第n-1到0 
    {
        if (i < n - 1)//如果是枚举最高位，第一类情况不存在，只有枚举的不是最高位，这种情况才存在 
        {
            res += get(num, n - 1, i + 1) * power10(i);
            if (!x) res -= power10(i);//也就是前导不能为 0，从00...01开始枚举，也就是减去00...0 
        }

        if (num[i] == x) res += get(num, i - 1, 0) + 1;//+1是因为可以都为0 
        else if (num[i] > x) res += power10(i);// >x的时候，后边可从00..0 ~ 99...9 
    }

    return res;
}

int main()
{
    int a, b;
    while (cin >> a >> b , a)
    {
        if (a > b) swap(a, b);

        for (int i = 0; i <= 9; i ++ )
            cout << count(b, i) - count(a - 1, i) << ' ';
        cout << endl;
    }

    return 0;
}

状态压缩dp

例题
解析引用一遍不错的博客
状压dp：状态压缩动态规划，指把利用二进制表示的集合当作状态，在此基础上进行dp

状态压缩就一个思想，就是用一个整数来表示某一个状态，整数的话，先把他当成一个二进制数，然后二进制数里面的每一个位是0是1表示两种不同情况

状态压缩的题目有一个特点，由于我们要把所有的不同的状态压缩到一个整数里面，所以不同的状态个数应该不会很多，一般n==20就是极限了，$2^{20}$就1e6了，所以很有特点，就看n比较小的时候能不能用状态压缩

也就是我们的状态虽然是一个整数，但是我们却需要把它看作一个二进制数，二进制数里面的每一位，是0是1表示不同的情况，一般不是很难，但是需要一些时间，来接受状态转移的方式和状态定义的方式
，思维难度比不上其他dp，理解套路就好

此题核心：先放横着的，再放竖着的，然后统计一下如果我们只放横着的小方块的话，合理的放法有多少种

当我们把横向小方格放完的时候，纵向一定只有一种方法，也就是，总方案数跟我们横向小方格摆放的方法一致
接着，开始求一下横向摆放小方格的方案数，这个可以按列来求，我们每一列用一个f[i,j]来表示
f[i,j]表示我现在要摆第i列，上一列中，横向摆放的小方格，压到第i列的个数为j个的情况下（如图这种，也就是，上一列中，哪些列伸出来了这样的一个小方格）的方案数，图中就是10000，

这里j是一个二进制的数，如图，图中j就是一个有五位（5行）的二进制数，可以表示0~31

对题目情况举个例子

第一个要注意的地方就是，不能冲突，从第i-1伸到第i列的 与 第i-2到i-1列的不能冲突，这个可以用位运算来判断，就是j&k是不是等于0，等于0就是没有冲突
第二个就是，所有剩余的连续格子一定得是偶数，也就是j|k不存在连续奇数个0，这个可以先预处理出来

只要满足这两个条件我们就可以把它们转移过来，就可以对应到我们的一种方案
然后遍历所有的k，看看是不是满足条件，加起来就行

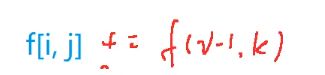
时间复杂度：状态数是11*$2^{11}$，转移状态的话，每一次需要计算$2^{11}$，一共4e7左右

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a) 
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define LL long long
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 12, M = 1<<N;
int n, m;//n和m表示行数和列数 
int f[N][M];//状态转移的方程
bool st[M]; 
signed main()
{
	fast;
	while (cin >> n >> m, n || m)//读入n和m，并且不是两个0即合法输入就继续读入
    {
    	//第一部分：预处理1
        //对于每种状态，先预处理每列不能有奇数个连续的0
        for (int i = 0; i < 1 << n; i ++ )
        {
            int cnt = 0;//记录连续的0的个数
            st[i] = true;// 假设它是成立的，没有奇数个连续的0则标记为true
            for (int j = 0; j < n; j ++ )//看每一行 ，也就是给了每一个状态比如1100..1然后看看每一行啥情况 
                if (i >> j & 1) //i（i在此处是一种状态）的二进制数的第j位； &1为判断该位是否为1，是1表示一个连续的0段结束了 
                {
                    if (cnt & 1) st[i] = false;//如果连续段里面0的个数是奇数，就不合法 
                    cnt = 0;//进入下一段 
                }
                else cnt ++ ;
            if (cnt & 1) st[i] = false;
        }
		//dp部分
		 
        memset(f, 0, sizeof f);
        f[0][0] = 1;//最一开始的时候，小方块里面还什么都没有放，第0列的时候，从前边捅过来是0的方案是唯一一种 
        for (int i = 1; i <= m; i ++ )//枚举一下所有的列 
            for (int j = 0; j < 1 << n; j ++ )//枚举一下所有的状态 
                for (int k = 0; k < 1 << n; k ++ )//枚举第i-1列的所有状态 
                    if ((j & k) == 0 && st[j | k])//判断一下两个条件 
                        f[i][j] += f[i - 1][k];
		//枚举到第m列的时候，应该凸出来的是0，才是合法方案
		//我的理解是，它是数的从0到m-1行，算是它的答案行，然后最多就是捅到m-1当然不会到m 
        cout << f[m][0] << endl;
    }
	return 0;
} 

例题2哈密顿
如果暴力的话，我们就应该找一个序列，就是访问的顺序
可以全排列一下，看一下路径长度，这个时间复杂度很高，不可取

状压dp：跟上一个思路类似，用一个整数表示状态
集合：所有从0号点走到j号点，走过的所有点是i的路径，i是二进制数，每一位就表示该点走没走过
状态计算：这里根据倒数第二个点是哪个点来分类，假设倒数第二个点是k，状态方程就得到了

然后对所有的k取一个min就行

#include 
#include 
#include 

using namespace std;

const int N = 20, M = 1 << N;

int n;
int w[N][N];//路径权值 
int f[M][N];

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            cin >> w[i][j];

    memset(f, 0x3f, sizeof f);
    f[1][0] = 0;//从0走到0，也就是00...1也就是1，终点是0，也就是f[1][0] 

    for (int i = 0; i < 1 << n; i ++ )
        for (int j = 0; j < n; j ++ )
            if (i >> j & 1)//走过的点里面必须要有j这个点才有意义 
                for (int k = 0; k < n; k ++ )
                    if (i >> k & 1)//表示走过这个点，而且倒数第二个点可以是这个点 
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);

    cout << f[(1 << n) - 1][n - 1];

    return 0;
}

树形dp

来个例题

集合f[u, 0]指的是所有以u为根的子树中选择，并且不选u这个点的方案， f[u, 1]指的是所有从以u为根的子树中选择，并且选u这个点的方案

求树形dp的时候，是从根节点开始递归求，递归到u这个点的时候，先把u的儿子处理好，也就是先算出来下面四个，算完之后再算f[u,0]；这里不选u这个点，所以最大值就是两个子树的最大值，得到状态表达式

时间复杂度：一共有2n个状态，每个状态枚举的时候需要枚举它每个儿子，所有节点儿子的数量加到一起就是边的数量，也就是n-1，所以计算所有的状态，我们枚举的次数一共是O（n），也就是时间复杂度O（n）
由于本题没有给根节点，所以需要自己求，没有父节点的点就是根节点

#include 
#include 
#include 

using namespace std;

const int N = 6010;

int n;
int h[N], e[N], ne[N], idx;
int happy[N];
int f[N][2];
bool has_fa[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u)
{
    f[u][1] = happy[u];

    for (int i = h[u]; ~i; i = ne[i])//~i等同于i!=-1 
    {
        int j = e[i];
        dfs(j);

        f[u][1] += f[j][0];
        f[u][0] += max(f[j][0], f[j][1]);
    }
}

int main()
{
    scanf("%d", &n);

    for (int i = 1; i <= n; i ++ ) scanf("%d", &happy[i]);

    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(b, a);//b是a的父节点 
        has_fa[a] = true;
    }

    int root = 1;
    while (has_fa[root]) root ++ ;//找父节点 

    dfs(root);

    printf("%d\n", max(f[root][0], f[root][1]));

    return 0;
}