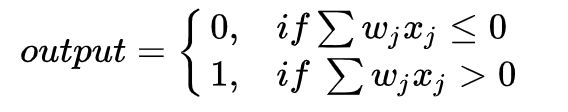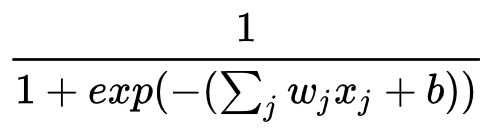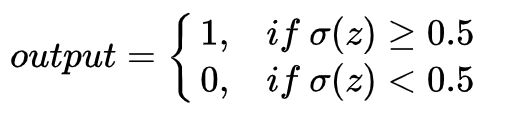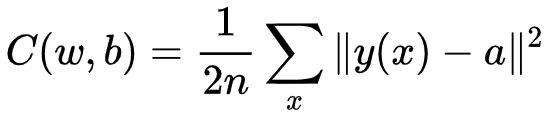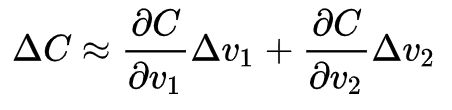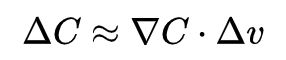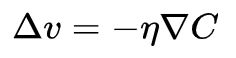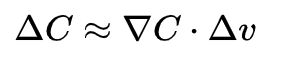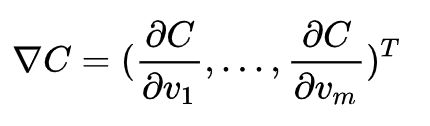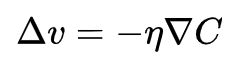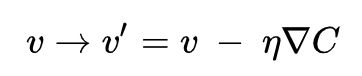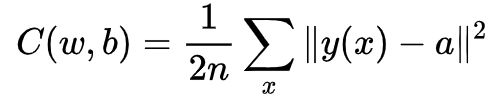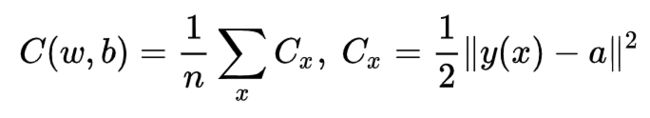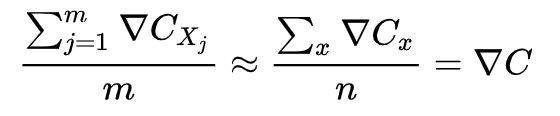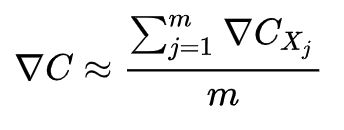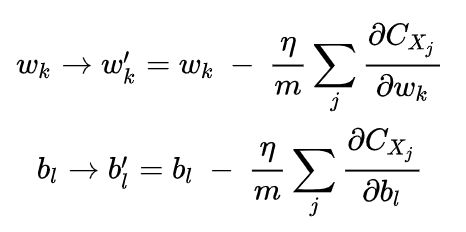简介
本文的目的是不借助任何深度学习算法库实现一个简单的3层全连接神经网络(FCN),并将其用于MNIST手写数字识别任务。
文章将依次介绍感知器模型、S型神经元、全连接神经网络结构、梯度下降等内容,并在最后给出完整代码。为了避免打击读者的信心,这里可以提前告诉大家,最后的代码除掉注释在100行之内。是不是觉得很兴奋?我们不借助其他神经网络库,仅仅使用少于100行的代码就可以实现一个简单的全连接神经网络,并且它在MNIST数据集上的识别正确率可以达到96%以上。
接下来就让我们开始进入正题吧!
神经网络概览
我们要设计的全连接神经网络的具体功能是,给定一张手写数字图片,神经网络要能识别出来这个数字是几。
听起来像很简单的任务是吗?但是如果使用传统的计算机程序来识别诸如上图中的数字,就会明显感受到视觉模式识别的困难。因为以往我们编写的计算机程序往往擅长处理各种提前制定好的规则。比如要读取一张图片,我们会先判断图片的格式,根据具体的格式解码出图像内容再显示出来。而对于数字识别这个任务,规则变得十分模糊与复杂,如果我们试着让这些识别规则变得越发精准的时候,就会很快陷入各种混乱的场景和异常情况中,这并不是一条可行的道路。
传统的方式行不通,那我们如何来解决这个问题呢?首先回想一下小时候我们是怎么学习认数字的,老师会把数字0~9挨个给我们看,然后告诉我们它们分别是几。如果我们不小心认错了,老师会即时纠正我们,经过一段时间的练习和记忆之后,我们就可以认得数字了。
神经网络也有异曲同工之妙,其思想是首先获取大量的手写数字去建立一个训练数据集,然后开发一个可以从这些训练数据中进行学习的系统,接着使用训练数据集去训练这个系统,最后系统便能够识别手写数字了。换言之,神经网络使用训练样本来自动推断出识别手写数字的规则。
根据上面的描述,可以归纳出构成全连接网络的几个要素:
- 训练数据集(MNIST)
- 可以从训练样本中自学习的系统(全连接网络结构)
- 训练系统的方法(梯度下降+反向传播)
接下来会分别从这几个方面来介绍。
MNIST
MNIST是一个手写数字集合,包含了60000张测试图片和10000张测试图片,每张图片分辨率为28x28,像素点数值取值范围0~255。MNIST 的名字来源于NIST——美国国家标准与技术研究所——收集的两个数据集改进后的子集,关于MNIST数据集更多信息可以自行搜索。
MNIST数据集在机器学习、深度学习领域的地位类似于各类编程语言里学的”Hello World“程序。
我们设计的神经网络并不会直接使用原始图像,而是会将其转换成向量的形式,即每张原始图像可以看做是一个28x28=784维的向量,向量中的每一维分别代表原始图像中对应像素点的灰度值。
全连接网络结构
感知器模型
在介绍全连接网络结构之前,我们先了解一下感知器模型。虽然我们最后的神经网络中并不包含这个模型,但是下面要介绍到的S型神经元是由感知器模型演变过去的,因此值得花点时间来理解下感知器。
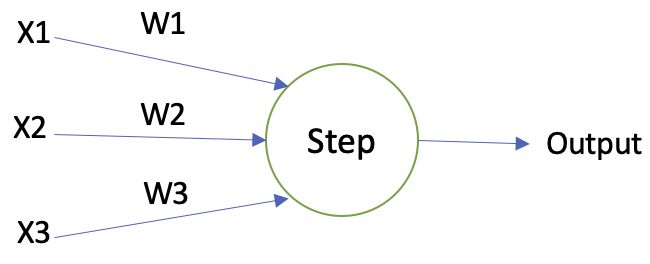
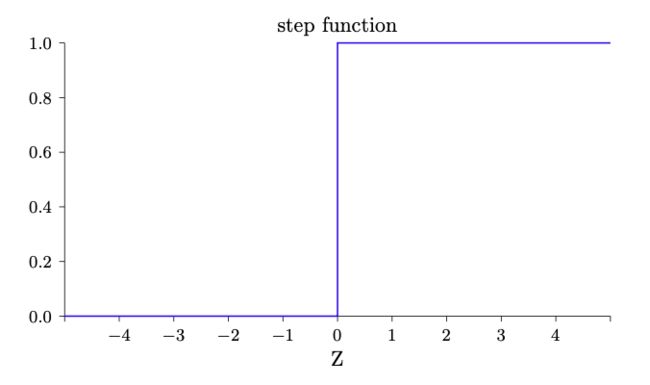
上图中的感知器有3个输入,。通常可以有更多或者更少输入。紧挨着的3条边分别代表3个权重,。圆圈里面是一个Step函数,Step函数的图像如下:
因此整个感知器模型的代数定义如下:直观地解释就是,对于每一个输入,将其乘上对应的权值,再累加起来得到一个中间结果,再将通过一个阶跃函数,如果大于0,则输出1;反之,输出0。这就是一个感知器所要做的全部事情。
这是一个基本的数学模型,你可以将感知器看做是一种可以根据权重来做出决定的机器。我们可以通过手动改变模型中的权重以及圆圈中的函数来得到不同的感知器模型,它们对同一输入可以做出不同的决策。
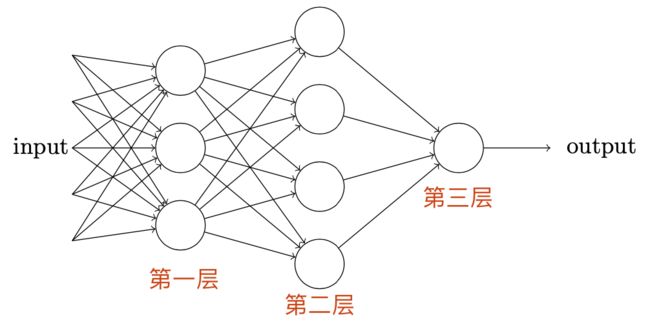
我们将上述的简单感知器进行组合,得到下面稍微复杂点的多层感知器模型:
在这个网络中,第一列感知器——我们称其为第一层感知器——通过权衡输入依据做出三个非常简单的决定。那第二层的感知器呢?每一个都在权衡第一层的决策结果并做出决定。以这种方式,一个第二层中的感知器可以比第一层中的做出更复杂和抽象的决策。在第三层中的感知器甚至能进行更复杂的决策。以这种方式,一个多层的感知器网络可以从事复杂巧妙的决策。
那这个模型跟我们的手写数字识别有什么关系呢?
换个角度来思考这个问题,既然感知器的输出是0或者1,那是不是意味着我们其实就可以用它来做单一手写数字图像分类呢?比如判断一张图像中的数字是不是”9“。如果图片显示的是“9”,就输出1,否则输出0。很显然,我们的感知器一开始并不知道如何判断图像是不是包含”9“,但是别忘了,我们可以修改权值和圆圈中的激活函数来让感知器做出正确的分类。
S型神经元
如果我们对权值或者激活函数中的偏置做出的微小改动就能够引起输出的微小变化,那我们就可以利用这一事实来修改权值和激活函数,让网络能够表现得像我们想要的那样。假设网络错误地把一个“9”的图像分类为“8”,我们能够计算出怎么对权重和偏置做些小的改动,这样网络能够接近于把图像分类为“9”。然后我们要重复这个工作,反复改动权重和偏置来产生更好的输出,此时网络其实就是在自我学习。
但是我们目前的感知器网络无法做到这一点。因为感知器的输出要么是0,要么是1。对权重和偏置的微小改动可能会让感知器的输出发生大反转,比如从0变成1。在多层感知器模型里面,这样的反转可能使得与此感知器连接的其余网络的行为完全改变。因此,也许”9“可以被正确分类,网络在其它图像上的行为很可能以一些很难控制的方式被完全改变。这使得逐步修改权重和偏置来 让网络接近期望行为变得困难。
因此我们引入一种称为S型神经元的新的人工神经元来克服这个问题,它与感知器类似,但是对权值和激活函数的偏置的微小改动只会引起输出的微笑改变,而不会像感知器那样完全反转。
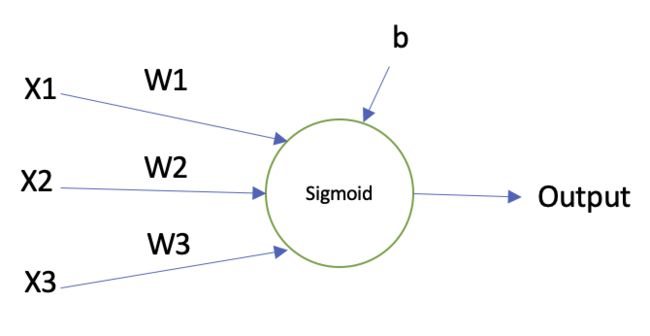
可以看到它与感知器模型非常类似,S 型神经元有多个输入,。这些输入可以是0和1中的任意值。同样S型神经元对每个输入都有权重,,和一个总的偏置b。但是它的输出不再是0或者1,而是,这里的也写成,的定义如下:
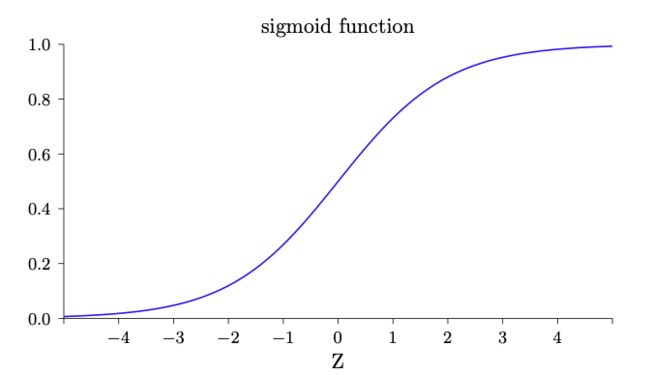
故上述模型的最终输出为:函数的图像如下:
为了理解和感知器模型的相似性,假设 是一个很大的正数,那么 , 而 。即当 很大并且为正,S 型神经元的输出近似为 1,正好和感知器一样。 相反地,假设 是一个很大的负数。那么 。所以当 是一个很大的负数,S 型神经元的行为也非常近似一个感知器。只有在 取中间值时,和感知器模型有比较大的偏离。 我们应该如何解释一个S型神经元的输出呢? 很明显感知器和 S 型神经元之间一个很大的不同是S型神经元不仅仅输出0或1,它可以输出0和1之间的任何实数。假设我们希望网络的输出是表示”输入图像是一个9“或”输入图像不是一个9“的话,此时网络输出0或者1会更容易表示这种情况。此时我们可以采用以下约定,即以0.5为分界点,将S型神经元的输出转换成0或者1,具体表述如下:
一个简单的分类手写数字的网络
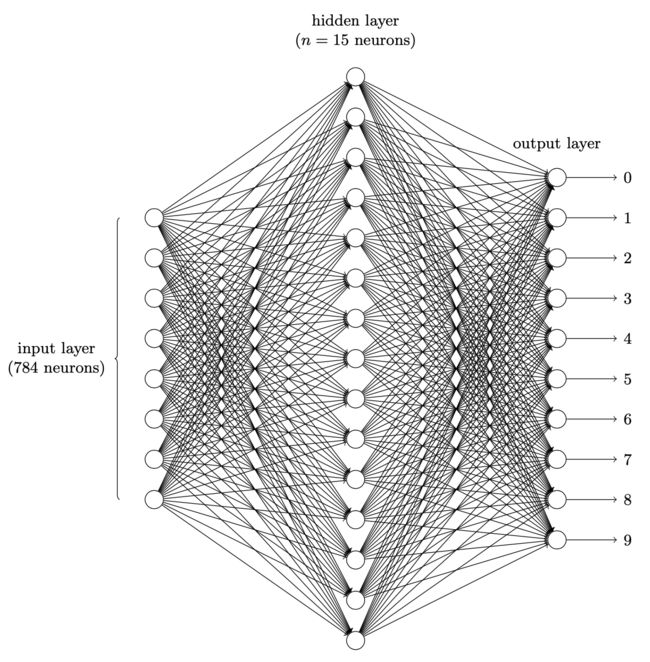
在理解基础神经元模型之后,我们就可以构建较为复杂的神经网络。本文中我们将使用一个3层的神经网络来识别单个数字,网络结构如下:网络的第一层是输入层,由于我们的输入数据是28x28的图像,将其摊平成28x28=784维的向量,所以输入层包含有784个神经元。为了简化,上图中忽略了 784 中大部分的输入神经元。输入像素是灰度级的, 值为 0.0 表示白色,值为 1.0 表示黑色,中间数值表示逐渐暗淡的灰色。
网络的第二层是一个隐藏层,仅仅包含了15个神经元,当然我们其实可以根据需要动态调整这个参数以观察不同隐藏层神经元个数对最终结果的影响。
网络的第三层是输出层,包含有 10 个神经元。如果第一个神经元激活,即输出 ≈ 1,那么表明网络认为数字是一个”0“。如果第二个神经元激活,就表明网络认为数字是一个”1“。依此类推。更确切地说, 我们把输出神经元的输出赋予编号 0 到 9,并计算出哪个神经元有最高的激活值。比如,如果编号为 6 的神经元激活,那么我们的网络会猜到输入的数字是”6“,其它神经元相同。
梯度下降
有了训练数据集和定义好的神经网络结构之后,它将怎样学习识别数字呢?
对于上图中的神经网络结构,假设我们随机初始化各个神经元的权值,并且将手写数字图片”9“传入到网络中,那么可以预见网络大概率并不会得到正确答案,但是我们可以通过不断调整权值来让它输出正确的结果。对于简单的模型也许这样做是可行的,因为毕竟可以调整的权重数据很少,但是对于我们定义的网络,它其中包含了784x15+15x10+15+10 = 11935个参数,手动修改简直是一场噩梦。
这里的代表的是网络中所有权重的集合,是所有的偏置,是训练输入数据的个数,是输入对应的标签,是表示当输入为时神经网络输出的向量,求和则是在总的训练输入上进行的。
我们把称之为二次代价函数,也称均方误差或者MSE。
通过观察可以发现,损失函数的值是非负的,因为求和公式中的每一项都是非负的。如果代价函数 的值相当小,即 ,那么意味着,对于所有的训练输入, 接近于神经网络输出。相反, 当很大时就不怎么好了,那意味着对于大量地输入,与输出相差很大。因此我们的训练算法的目的,是要最小化代价函数,使。
现在我们忘掉之前讲过的各种神经元、网络结构、MNIST等等,把注意力集中在一个问题上,那就是如何最小化一个给定的多元函数?我们使用一种被称之为梯度下降的技术来解决这样的最小化问题。
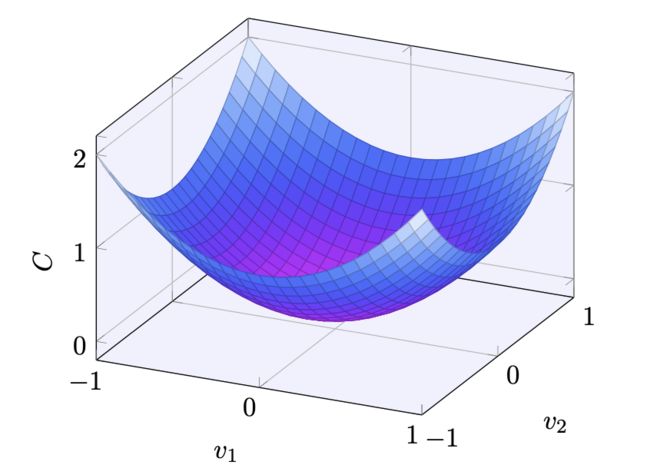
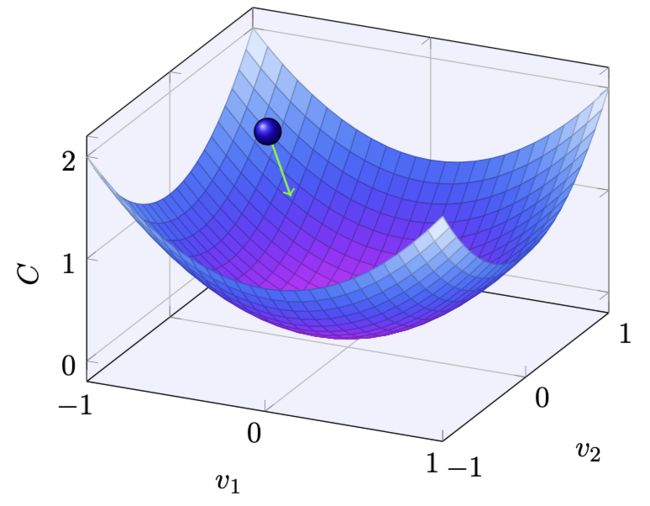
假设我们要最小化某些函数,如。它可以是任意的多元实值函数,。 注意我们用 代替了 和 以强调它可能是任意的函数,这里我们以只有两个变量,的二元函数举例,图像如下:
这里你也许会问为什么拿二元函数举例,主要原因是因为可以将其可视化,如果包含两个自变量以上的话,我们就无法画出它对应的图像了。
从图中可以一眼看到 的最小值在(0,0)处取得,但是通常函数 是一个复杂的多元函数,远不止2个自变量,因此看一眼就能找到最小值是不太现实的,此时梯度下降法就可以发挥用处了。
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的,而是需要一个复杂的工具来测量,同时,这个人此时正好拥有测量出最陡峭方向的能力。所以,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率,来确保下山的方向不错误,同时又不至于耗时太多!
关于梯度下降法的详细解释可以参考这篇博客,写的非常详细,强烈推荐。
回到我们的问题中来,首先把我们的函数想象成一个山谷,现在有一个人被困在了山上的某一处。现在我们让这个人沿着和方向移动一个很小的量,即和,微积分告诉我们函数将会有如下变化:
为了使往更小的方向变化,我们需要寻找一种选择和的方法使得为负,即让小人往下山的方向走。为了弄明白如何选择,需要定义为的变化的向量,即是转置符号。我们也定义的梯度为偏导数的向量,。我们使用来表示梯度向量,即:
有了这些定义,的表达式可以被重写成:
这个表达式解释了为什么 被称为梯度向量: 把 的变化关联为 的变化,正如我们期望的用梯度来表示,但是这个方程真正让我们兴奋的是它让我们看到了如何选取 才能让 变为负数。假设我们选取:
这里的是一个很小的数,称之为学习率。那么。由于,这就可以保证,即如果我们按照上式的规则去改变自变量,那么就会一直减小,即小人会一直往下山的方向移动。我们令代表改变后的新的自变量,将上式展开得到:
由此我们得到了自变量的更新方式,可以使用它来计算下一次的移动方向和距离。如果我们反复这么做,那么我们将持续减小,正如我们希望的,得到一个全局的最小值。
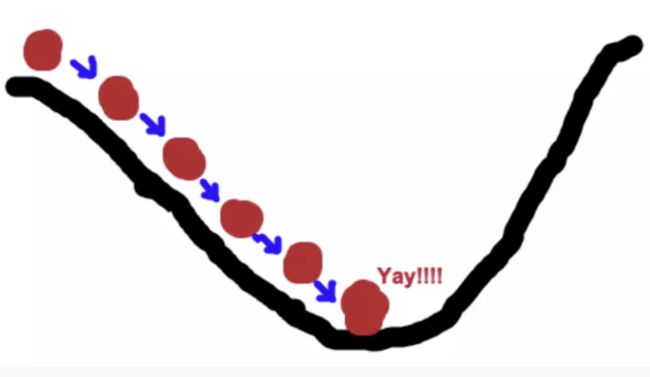
总结一下,梯度下降算法工作的方式就是重复计算梯度 ,然后沿着相反的方向移动。我们可以想象它像这样:
这里需要介绍一下上面提到的学习率,可以看到它的主要功能是用来控制小人每次移动的步长。如果太大,那么每次的变化很剧烈,即小人每次迈的步子很大,那么当小人很快就要到谷底的时候,结果因为步子迈得太大,错过了最低点,这肯定不是我们希望看到的。同理,我们也不希望太小,那意味着每次变化很小,即小人迈的步子很小,行动缓慢,这就导致需要花很长时间才能到达谷底。因此在真正的实现中,通常是变化的。比如我们希望在一开始比较大,而快到谷底的时候稍微变小点,即小人最开始大步往山下走,当快到谷底的时候,小心翼翼地挪动步伐,防止错过谷底。
我们解释了只有两个自变量的函数的梯度下降算法,但事实上,即使是一个具有多个变量的函数时,梯度下降算法也能很好地工作。假设是一个具有m个变量的多元函数。那么对中的自变量的变化,会变成:
这里的梯度是向量:
正如两个自变量的情况,我们可以选取:自变量的更新规则为:
至此,梯度下降算法就介绍完毕了。
随机梯度下降算法
我们怎么在神经网络中使用梯度下降算法去学习呢?其思想就是利用梯度下降算法寻找使得我们的全连接神经网络的损失函数取得最小值时的权重和。我估计你肯定忘了我们的损失函数是什么了,我将其重新写在下面:
相比之前的函数,这里相当于把原先的自变量和换成了和,而梯度向量则变成了 和。用这些分量来写梯度下降的更新规则,可以得到:
注意不要认为我们的损失函数也是只有两个变量和哦
你可能注意到了这一节的标题叫做随机梯度下降,既然上一节已经有了梯度下降,怎么又来个随机梯度下降?
其中代表的是一个训练样本的损失函数,也就是是总体的损失函数是对每一个训练样本的损失函数的值累加之后再求平均。故为了计算梯度,我们需要遍历整个训练数据集,对每一个训练样本都计算梯度,然后累加之后求平均值。这样导致的最直接的问题就是当好训练集很大的时候,训练速度会非常的慢。
为了加速训练过程,在实际使用中,我们会采用随机梯度下降的算法。它的原理也非常朴素,就是我们不采用整个数据集,而是随机选取小量训练样本来计算梯度,进而估算实际梯度。通过计算少量样本的平均值我们就可以快速得到一个对于实际梯度很好的估算,这有助于加速梯度下降,进而加快训练过程。
再用小人下山的例子来对比一下梯度下降算法和随机梯度下降算法。假设小人使用梯度下降算法下山,那意味着小人每走一步之前,都需要经过精确的计算以便找到最陡峭的方向,然后沿着这个方向迈出一步,毕竟按照这个方向下山肯定是最快的。而如果小人使用随机梯度算法下山的话,他并不会花那么长的时间去找到最陡峭的方向,而是找到一个大概的方向就行了,然后就快速地迈出一步。毕竟只要方向基本不错,最终肯定也能到达谷底。
随机梯度下降通过随机选取小量的 m 个训练样本来工作。我们将这些随机的训练样本标记为 ,并把它们称为一个小批量数据(mini-batch)。假设样本数量 m 足够大,我们期望 的平均值大致相等于整个 的平均值,即:
交换两边我们得到:证实了我们可以仅仅计算随机选取的小批量数据的梯度来估算整体梯度。
为了明确地和神经网络的学习联系起来,假设和表示我们神经网络中的权重和偏置,随机梯度下降通过随机地选取小批量的训练样本来工作,因此我们可以更改一下梯度下降的更新规则:
其中两个求和符号是在当前小批量数据中的所有训练样本 上进行的。我们随机挑选若干个小批量数据集,然后以此用这些小批量数据集去训练网络,当用完了全部的小批量数据集之后,这被称为完成了一次迭代周期(epoch),然后开始新一轮的训练迭代周期。
反向传播
限于篇幅,略过,详情请看这篇博客。
代码实践
本文采用的代码来自Github,但是原作者是基于Python2.7写的,我用python3将其改写了一遍,并且加上了很多注释。
代码链接在https://github.com/HeartbreakSurvivor/ClassicNetworks/tree/master/FCN
总共包含3个文件,分别是"mnist_loader.py"、"fc.py"、"mnist.pkl.gz"。
下面展示实现了神经网络的fc.py的内容:
import random
import numpy as np
import mnist_loader
def sigmoid(z):
"""
Sigmoid激活函数定义
"""
return 1.0/(1.0 + np.exp(-z))
def sigmoid_prime(z):
"""
Sigmoid函数的导数,关于Sigmoid函数的求导可以自行搜索。
"""
return sigmoid(z)*(1-sigmoid(z))
class FCN(object):
"""
全连接网络的纯手工实现
"""
def __init__(self, sizes):
"""
:param sizes: 是一个列表,其中包含了神经网络每一层的神经元的个数,列表的长度就是神经网络的层数。
举个例子,假如列表为[784,30,10],那么意味着它是一个3层的神经网络,第一层包含784个神经元,第二层30个,最后一层10个。
注意,神经网络的权重和偏置是随机生成的,使用一个均值为0,方差为1的高斯分布。
注意第一层被认为是输入层,它是没有偏置向量b和权重向量w的。因为偏置只是用来计算第二层之后的输出
"""
self._num_layers = len(sizes) # 记录神经网络的层数
# 为隐藏层和输出层生成偏置向量b,还是以[784,30,10]为例,那么一共会生成2个偏置向量b,分别属于隐藏层和输出层,大小分别为30x1,10x1。
self._biases = [np.random.randn(y, 1) for y in sizes[1:]]
# 为隐藏层和输出层生成权重向量W, 以[784,30,10]为例,这里会生成2个权重向量w,分别属于隐藏层和输出层,大小分别是30x784, 10x30。
self._weights = [np.random.randn(y, x) for x,y in zip(sizes[:-1], sizes[1:])]
# print(self._biases[0].shape)
# print(self._biases[1].shape)
# print(self._weights[0].shape)
# print(self._weights[1].shape)
def feedforward(self, a):
"""
前向计算,返回神经网络的输出。公式如下:
output = sigmoid(w*x+b)
以[784,30,10]为例,权重向量大小分别为[30x784, 10x30],偏置向量大小分别为[30x1, 10x1]
输入向量为 784x1.
矩阵的计算过程为:
30x784 * 784x1 = 30x1
30x1 + 30x1 = 30x1
10x30 * 30x1 = 10x1
10x1 + 10x1 = 10x1
故最后的输出是10x1的向量,即代表了10个数字。
:param a: 神经网络的输入
"""
for b, w in zip(self._biases, self._weights):
a = sigmoid(np.dot(w, a) + b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None):
"""
使用小批量随机梯度下降来训练网络
:param training_data: training data 是一个元素为(x, y)元祖形式的列表,代表了训练数据的输入和输出。
:param epochs: 训练轮次
:param mini_batch_size: 小批量训练样本数据集大小
:param eta: 学习率
:param test_data: 如果test_data被指定,那么在每一轮迭代完成之后,都对测试数据集进行评估,计算有多少样本被正确识别了。但是这会拖慢训练速度。
:return:
"""
if test_data: n_test = len(test_data)
n = len(training_data)
for j in range(epochs):
# 在每一次迭代之前,都将训练数据集进行随机打乱,然后每次随机选取若干个小批量训练数据集
random.shuffle(training_data)
mini_batches = [training_data[k:k+mini_batch_size] for k in range(0, n, mini_batch_size)]
# 每次训练迭代周期中要使用完全部的小批量训练数据集
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
# 如果test_data被指定,那么在每一轮迭代完成之后,都对测试数据集进行评估,计算有多少样本被正确识别了
if test_data:
print("Epoch %d: accuracy rate: %.2f%%" % (j, self.evaluate(test_data)/n_test*100))
else:
print("Epoch {0} complete".format(j))
def update_mini_batch(self, mini_batch, eta):
"""
通过小批量随机梯度下降以及反向传播来更新神经网络的权重和偏置向量
:param mini_batch: 随机选择的小批量
:param eta: 学习率
"""
nabla_b = [np.zeros(b.shape) for b in self._biases]
nabla_w = [np.zeros(w.shape) for w in self._weights]
for x,y in mini_batch:
# 反向传播算法,运用链式法则求得对b和w的偏导
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
# 对小批量训练数据集中的每一个求得的偏导数进行累加
nabla_b = [nb + dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw + dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
# 使用梯度下降得出的规则来更新权重和偏置向量
self._weights = [w - (eta / len(mini_batch)) * nw
for w, nw in zip(self._weights, nabla_w)]
self._biases = [b - (eta / len(mini_batch)) * nb
for b, nb in zip(self._biases, nabla_b)]
def backprop(self, x, y):
"""
反向传播算法,计算损失对w和b的梯度
:param x: 训练数据x
:param y: 训练数据x对应的标签
:return: Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``.
"""
nabla_b = [np.zeros(b.shape) for b in self._biases]
nabla_w = [np.zeros(w.shape) for w in self._weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self._biases, self._weights):
# z = wt*x+b note that the shape of z is the same as the bias
z = np.dot(w, activation) + b
zs.append(z)
activation = sigmoid(z) #pass the result z to activator function --> a = sigmoid(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
for l in range(2, self._num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self._weights[-l + 1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l - 1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
"""
返回神经网络对测试数据test_data的预测结果,并且计算其中识别正确的个数
因为神经网络的输出是一个10x1的向量,我们需要知道哪一个神经元被激活的程度最大,
因此使用了argmax函数以获取激活值最大的神经元的下标,那就是网络输出的最终结果。
"""
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""
返回损失函数对a的的偏导数,损失函数定义 C = 1/2*||y(x)-a||^2
求导的结果为:
C' = y(x) - a
"""
return (output_activations - y)
if __name__ == "__main__":
# 获取MNIST训练数据集、验证数据集、测试数据集
training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
# 定义一个3层全连接网络,输入层有784个神经元,隐藏层30个神经元,输出层10个神经元
fc = FCN([784, 30, 10])
# 设置迭代次数30次,mini-batch大小为10,学习率为3,并且设置测试集,即每一轮训练完成之后,都对模型进行一次评估。
# 这里的参数可以根据实际情况进行修改
fc.SGD(training_data, 30, 10, 3.0, test_data=test_data)
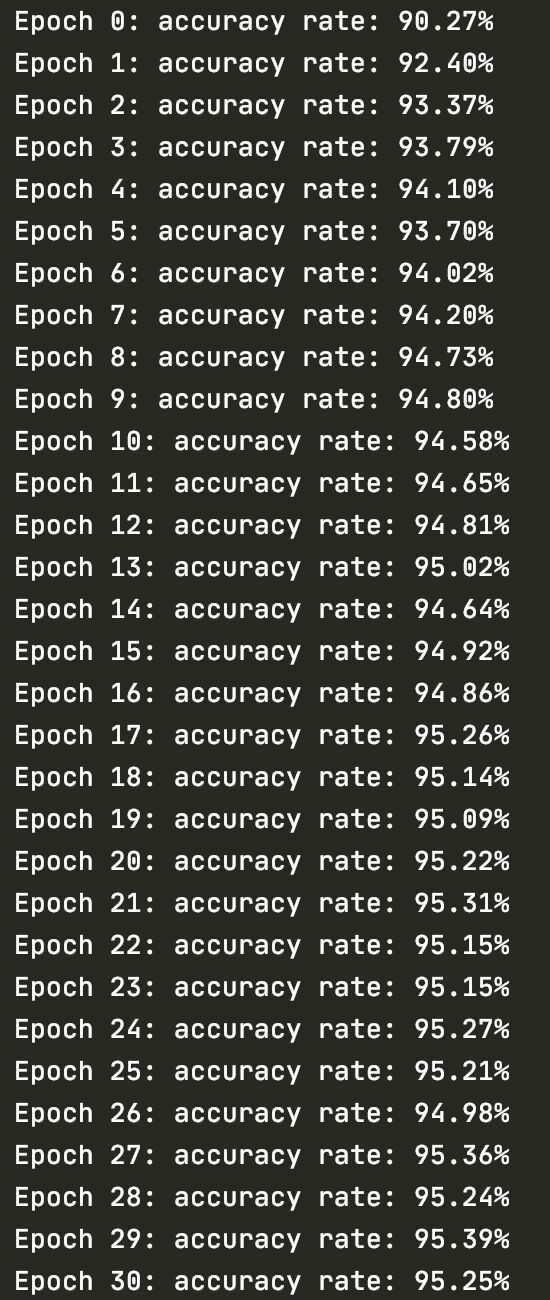
上述代码定义了一个3层的全连接神经网络,每层包含的神经元个数分别为784、30、10。训练迭代周期为30,小批量数据集个数为10,学习率为3.0。并且设置了测试数据集,即每完成一个训练迭代周期之后,都会将测试数据集运用在神经网络上用来计算手写数字识别准确率,经过30次的迭代周期之后,最终达到了95.25%的识别正确率。
因为神经网络的权重和偏置是随机生成的,故每次试验结果并不一样。感兴趣的读者可以在自己的电脑上跑一下代码,并且可以修改一下隐藏层神经元数量、迭代周期、学习率、小批量训练集的数量等,观察一下神经网络计算出来的正确率会发生什么变化。
总结
本文篇幅很长,但是若能仔细阅读并且对文中提及的公式都手动推导一遍,再结合代码调试一下的话,相信会对全连接神经网络的原理和训练优化过程有较为深刻的理解。
后记
本文是自己学习《神经网络与深度学习》第一章内容时做的笔记。原文讲解的非常详细生动,但是篇幅也很长,我提炼了出其中最主要的部分记录下来,方便自己查阅以及他人学习。
个人觉得这本书写的非常不错,以非常浅显的语言与生动的图例解释清楚了全连接神经网络的构成、训练、优化、调参等。GitHub上有对应的中文版,感兴趣的读者也可以看这本。不过还是非常推荐阅读英文原版,因为原文是基于网页的,有很多形象的插图、动画以及在线程序演示等,可以使读者加深对全连接网络的印象。
参考
- 《神经网络与深度学习》
- https://github.com/mnielsen/neural-networks-and-deep-learning
- https://www.jianshu.com/p/c7e642877b0e
- https://www.jianshu.com/p/25f0139637b7
- https://www.zybuluo.com/codeep/note/163962#5%E5%BE%AE%E7%A7%AF%E5%88%86%E8%BF%90%E7%AE%97%E7%AC%A6