机器学习——决策树算法之代码+数学实例解析

1、文章简介

       写该文章，主要借阅的资料有：
       ①《python机器学习基础教程》
       ②《机器学习基础：从入门到求职》
       ③以及学习一些网上的资料案例整理
       需要安装的环境：
       ①安装绘图工具 Graphviz：https://www.cnblogs.com/shuodehaoa/p/8667045.html
       ②安装机器学习本篇必需的库：matplotlib，scikit-learn。（本篇外一般还会安装numpy，scipy，pandas等）

2、决策树简单概述

       决策树（Decision Tree）是一种树状结构模型，可以进行基本的分类与回归。
       决策树常听到的名词有：ID3决策树、C4.5决策树、CART决策树。其中采用的核心思想如下：
       ①ID3决策树采用信息增益来进行计算；
       ②C4.5决策树采用信息增益比(率)进行计算；
       ③CART决策树采用基尼系数进行计算。
       本文涉及到的决策树是CART决策树，由于文章篇幅问题，将不对ID3决策树、C4.5决策树进行讲解，网上也有很多资料，由于CART决策树已经是上面两种决策树的升级版，所以推荐数学实例学习资料(先学学公式)：
       ①ID3决策树：https://www.cnblogs.com/gfgwxw/p/9439482.html；
       ②C4.5决策树：https://blog.csdn.net/qq_28697571/article/details/84679852；

3、决策树代码实例讲解

（1）实例

       针对14位路人的年龄特征（age）、收入情况（income）、是否英俊（handsome）、性格特点（character），以及是否拥有爱情构造一颗CART决策树。（注意：本例由于数据是自己造的，且样本较少，没有分为训练集和测试集，也就没有对数据的精度进行验证，14条数据全部作为训练集进行模型训练，最终直接将训练后的模型对新数据进行预测。）

（2）模型结果

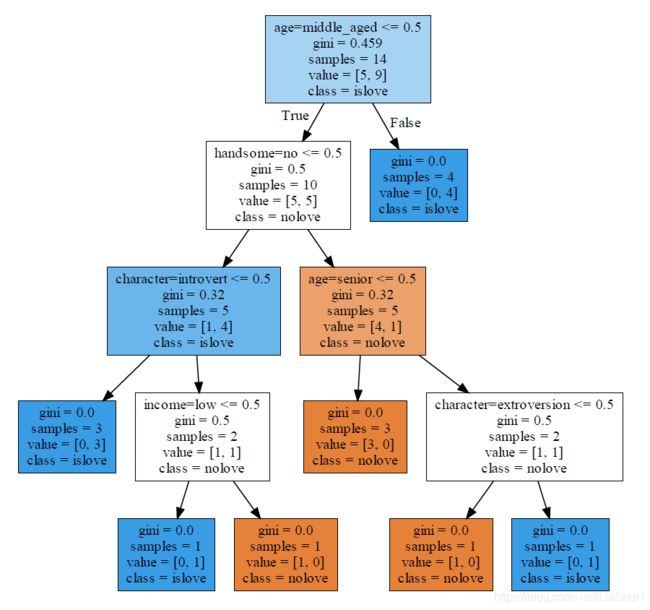
       由上图可知：gini=0.459代表基尼系数为0.459，sample=14说明有14个样本，value=[5,9]说明样本有两类，一类有5个样本为nolove，另一类为9个样本为islove。class=islove说明islove的样本数较多。

（3）准备数据

       这里将数据写入到csv(逗号分隔)文件love.csv，具体数据如下：

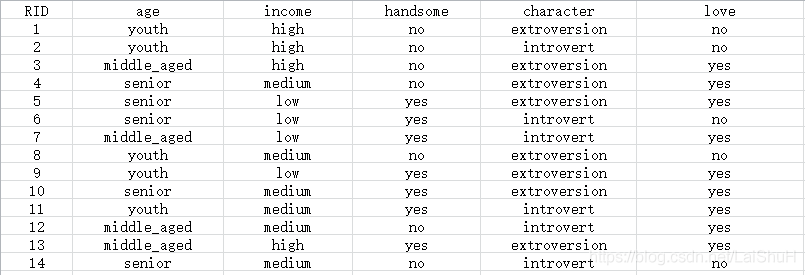
       其中，第一行为字段名称，第1列为序号，其他为数据内容。

（4）代码实现

import graphviz
import matplotlib
from sklearn import datasets, tree
# 导入可视化包
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.feature_extraction import DictVectorizer
from sklearn import preprocessing
from sklearn.tree import DecisionTreeClassifier

if __name__ == '__main__':
	getLove()  # 是否拥有爱情

# 是否拥有爱情
def getLove():
    loveData = open('D:\Python\Project\love.csv', 'r')
    reader = csv.reader(loveData)
    header = next(reader)
    featureList = []  # 存放每一行数据，每一行数据为一个字典，如一行数据：{'age': 'youth', 'income': 'high', 'handsome': 'no', 'character': 'extroversion'}
    labelList = []  # 存放历史数据的结果，即数据的最后一列
    for row in reader:
        labelList.append(row[len(row) - 1])  # 最后一列,存放样本的结果列
        rowDict = {}  # 存放字典，如{"age" : "youth"}
        for i in range(1, len(row) - 1):
            rowDict[header[i]] = row[i]
        featureList.append(rowDict)
    print(featureList)
    print(labelList)  # 输出是：['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']

    # 特征向量化、字典特征提取
    # 将一个数据集表示成一种只包含有数值型数据的一个list,然后就可以用于机器学习的计算
    vec = DictVectorizer()
    dummyX = vec.fit_transform(featureList).toarray()  # vec.fit_transform(featureList)返回的类型是scipy.sparse.csr.csr_matrix，可以和ndarray互转
    print(str(dummyX))
    print(vec.get_feature_names())

    # 标签二值化,可以把yes和no转化为0和1,将最后一列分类进行转化
    lb = preprocessing.LabelBinarizer()
    dummyY = lb.fit_transform(labelList)
    print(labelList)  # ['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
    print(str(dummyY))  # [[0][0][1][1][1][0][1][0][1][1][1][1][1][0]]
    
    # 构造CART树,使用基尼系数
    clf = tree.DecisionTreeClassifier(criterion='gini')  # criterion='entropy'代表信息熵
    clf.fit(dummyX, dummyY)
    
    # 将训练结果写入文件
    tree.export_graphviz(clf, class_names=["nolove", "islove"], feature_names=vec.feature_names_, out_file="clf.dot", filled=True)

    # 将训练结果读出展示
    with open("clf.dot", "r") as f:
        dot_graph = f.read()
    dot = graphviz.Source(dot_graph)
    dot.view()

    # predict 预测，利用训练数据的向量化规则对预测数据进行特征向量化
    predict = [{'age': 'middle_aged', 'income': 'high', 'handsome': 'no', 'character': 'extroversion'}]
    X_predict = vec.transform(predict)  # 如果使用fit_transform相当于重新将特征重新放入新的列表，使用transform是按照训练集的特征模板进行特征向量转化。
    print("X_X_predict:" + str(X_predict))
    y_X_predict = clf.predict(X_predict)
    print("y_X_predict:" + str(y_X_predict)  # y_X_predict:[1]
	print(lb.inverse_transform(y_X_predict))  # 标签你过程，输出['yes']
	#最终预测该位幸运儿拥有爱情！

（5）代码片段讲解

       ① 特征向量化、字典特征提取，该代码块主要将特征转换成计算机计算的0，1数字。会将所有特征放进一个列表，如：[‘age=middle_aged’, ‘age=senior’, ‘age=youth’, ‘character=extroversion’, ‘character=introvert’, ‘handsome=no’, ‘handsome=yes’, ‘income=high’, ‘income=low’, ‘income=medium’]无序，此时再将每一行数据根据该列表进行0，1赋值形成矩阵。如：第一行[0. 0. 1. 1. 0. 1. 0. 1. 0. 0.]表示：[youth,extroversion,no, high]。对于dummyY同理。

# 特征向量化、字典特征提取
# 将一个数据集表示成一种只包含有数值型数据的一个list,然后就可以用于机器学习的计算
vec = DictVectorizer()
dummyX = vec.fit_transform(
    featureList).toarray()  # vec.fit_transform(featureList)返回的类型是scipy.sparse.csr.csr_matrix，可以和ndarray互转
print(vec.get_feature_names())
# 输出：
# ['age=middle_aged', 'age=senior', 'age=youth', 'character=extroversion', 'character=introvert', 'handsome=no', 'handsome=yes', 'income=high', 'income=low', 'income=medium']
print(str(dummyX))
# 输出：
# [[0. 0. 1. 1. 0. 1. 0. 1. 0. 0.]
#  [0. 0. 1. 0. 1. 1. 0. 1. 0. 0.]
#  [1. 0. 0. 1. 0. 1. 0. 1. 0. 0.]
#  [0. 1. 0. 1. 0. 1. 0. 0. 0. 1.]
#  [0. 1. 0. 1. 0. 0. 1. 0. 1. 0.]
#  [0. 1. 0. 0. 1. 0. 1. 0. 1. 0.]
#  [1. 0. 0. 0. 1. 0. 1. 0. 1. 0.]
#  [0. 0. 1. 1. 0. 1. 0. 0. 0. 1.]
#  [0. 0. 1. 1. 0. 0. 1. 0. 1. 0.]
#  [0. 1. 0. 1. 0. 0. 1. 0. 0. 1.]
#  [0. 0. 1. 0. 1. 0. 1. 0. 0. 1.]
#  [1. 0. 0. 0. 1. 1. 0. 0. 0. 1.]
#  [1. 0. 0. 1. 0. 0. 1. 1. 0. 0.]
#  [0. 1. 0. 0. 1. 1. 0. 0. 0. 1.]]

       ② 画图，并展示：此处为了让树的图形更容易看，将结果分类的名字用[“nolove”, “islove”]来表示，对于tree.export_graphviz的用法以及参数、graphviz的用法这里不做详解，有兴趣的小伙伴可以查看相关文档资料进行学习。

 # 将训练结果写入文件
tree.export_graphviz(clf, class_names=["nolove", "islove"], feature_names=vec.feature_names_, out_file="clf.dot", filled=True)

# 将训练结果读出展示
with open("clf.dot", "r") as f:
    dot_graph = f.read()
dot = graphviz.Source(dot_graph)
dot.view()

4、决策树数学实例讲解

       看完上述代码跟树图是否还是很疑惑？这颗树是怎么出来的呢？使用机器学习的库是挺爽的，不用知道具体细节实现，但是就是不知道这棵树是怎么出来的，难受。没事，下面就告诉你，这颗树是怎么生成的。

（1）基尼系数简介

       a.概念：基尼系数（Gini）可以用来度量任何不均匀分布，且介于0~1之间的数（0指完全相等，1指完全不相等）。分类度量时，总体包含的类别越杂乱，基尼系数就越大（与熵的概念相似）。
       b.特点：基尼指数主要用来度量数据集的不纯度。基尼指数越小，表明样本只属于同一类的概率越高，即样本的纯净度越高。在计算出数据集某个特征所有取值的基尼指数后，就可以得到利用该特征进行样本划分产生的基尼指数增加值（GiniGain）；决策树模型在生成的过程中就是递归选择GiniGain 最小的节点作为分叉点，直至子数据集都属于同一类或者所有特征用光。
       c.公式：在分类问题中，假设有K个类别c1,c2,…,cK，样本点属于第k类的概率为pk，则该概率分布的基尼系数定义为:
                                                 
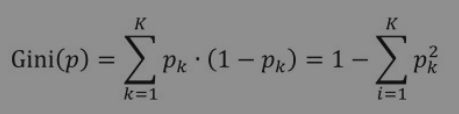
       对于给定的样本集合D，其基尼系数为:
                                                  

       对于只有两种类别的数据集，其基尼系数为:
                                         

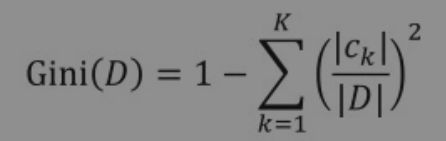
（2）求解上述实例

       第一步：
       首先计算各个特征的基尼系数。分别以A1, A2, A3, A4代表age,income,handsome,character情况的4个特征，并以1,2,3表示age的值为：youth,middle_age,senior；以1,2,3表示income的值为：high,medium,low；以1,2表示handsome的no,yes；以1,2表示character的extroversion,introvert。数据样本如下：

RID	 age	    income	handsome	 character	    love
 1	youth	     high	   no	    extroversion	 no
 2	youth	     high	   no	    introvert	     no
 3	middle_aged	 high	   no	    extroversion	 yes
 4	senior	    medium	   no	    extroversion	 yes
 5	senior	     low	   yes	    extroversion	 yes
 6	senior	     low	   yes	    introvert	     no
 7	middle_aged	 low	   yes	    introvert	     yes
 8	youth	    medium	   no	    extroversion	 no
 9	youth	     low	   yes	    extroversion	 yes
 10	senior	    medium	   yes	    extroversion	 yes
 11	youth	    medium	   yes	    introvert	     yes
 12	middle_aged	medium	   no	    introvert	     yes
 13	middle_aged	 high	   yes	    extroversion	 yes
 14	senior	    medium	   no	    introvert	     no

       ①计算整体数据的基尼系数：因为有9人拥有爱情，5人没有拥有爱情，所以p(k) = 9/14。所以求解如下，此系数为树中根节点的gini=0.459
            
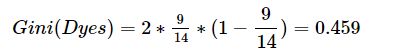
       ②求特征A1的基尼系数：因为A1=1=youth，所以将数据分为两类。一类A1=1，另一类A1=2、A1=3。其中A1=1类有5条数据，有2条拥有爱情；A1=2、A1=3类9条数据，有7条拥有爱情，所以计算如下（A1=2,A1=3的计算与A1=1原理一致）：
       ③求特征A2的基尼系数：因为A2=1=high，所以将数据分为两类。一类A2=1，另一类A2=2、A2=3。其中A2=1类有4条数据，有2条拥有爱情；A2=2、A2=3类10条数据，有7条拥有爱情，所以计算如下（A2=2,A2=3的计算与A2=1原理一致）：

       ④求特征A3的基尼系数：原理同上。

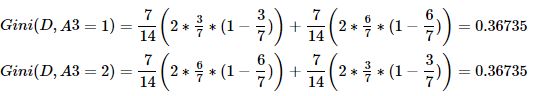
       ⑤求特征A4的基尼系数：原理同上。

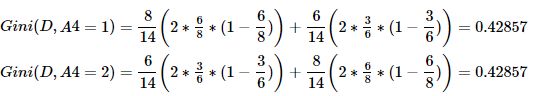
       综上，Gini(D,A1=2)=0.35714 最小，所以选择特征A1为最优特征，A1=2=middle_age为最优切分点（即根节点）。由于Gini(A1=2)=0,所以该子节点为纯叶子节点。另一节点继续使用上述方法求基尼系数。下面为两个结点的数据：

#Gini(A1=2)=0,所以该子节点为纯叶子节点
RID	 age	    income	handsome	 character	    love
 3	middle_aged	 high	   no	    extroversion	 yes
 7	middle_aged	 low	   yes	    introvert	     yes
 12	middle_aged	medium	   no	    introvert	     yes
 13	middle_aged	 high	   yes	    extroversion	 yes

#另一不纯结点继续使用上述方法求基尼系数
RID	 age	    income	handsome	 character	    love
 1	youth	     high	   no	    extroversion	 no
 2	youth	     high	   no	    introvert	     no
 4	senior	    medium	   no	    extroversion	 yes
 5	senior	     low	   yes	    extroversion	 yes
 6	senior	     low	   yes	    introvert	     no
 8	youth	    medium	   no	    extroversion	 no
 9	youth	     low	   yes	    extroversion	 yes
 10	senior	    medium	   yes	    extroversion	 yes
 11	youth	    medium	   yes	    introvert	     yes
 14	senior	    medium	   no	    introvert	     no

       第二步：计算剩下数据的基尼系数。
       ①计算整体数据的基尼系数：因为有5人拥有爱情，5人没有拥有爱情，所以p(k) = 5/10。所以求解如下，此系数为树中该分支根节点的gini=0.5。

       ②求特征A1的基尼系数：原理同上。

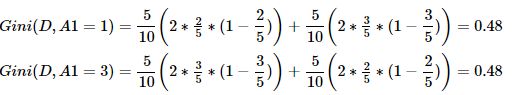
       ③求特征A2的基尼系数：原理同上。

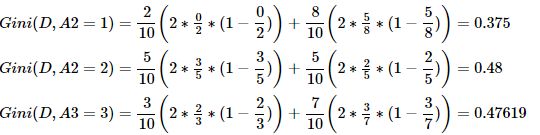
       ④求特征A3的基尼系数：原理同上，由于A3特征只有2个类别，所以Gini系数是相等的（其实上面也一样，只要是只有yes和on的都是相等的），所以用以下写法简写。

       ⑤求特征A4的基尼系数：原理同上。

       综上，Gini(D,A3=1,2)=0.32 最小，所以选择特征A3为最优特征，A3=1=no为最优切分点（即子树根节点）。由于Gini(A3=1)=0.32,所以该根节点的两个子节点都不纯，继续使用上述方法求基尼系数。下面为两个结点的数据：

# 左子树数据
RID	 age	    income	handsome	 character	    love
 5	senior	     low	   yes	    extroversion	 yes
 6	senior	     low	   yes	    introvert	     no
 9	youth	     low	   yes	    extroversion	 yes
 10	senior	    medium	   yes	    extroversion	 yes
 11	youth	    medium	   yes	    introvert	     yes

# 右子树数据
RID	 age	    income	handsome	 character	    love
 1	youth	     high	   no	    extroversion	 no
 2	youth	     high	   no	    introvert	     no
 4	senior	    medium	   no	    extroversion	 yes
 8	youth	    medium	   no	    extroversion	 no
 14	senior	    medium	   no	    introvert	     no

       第三步：计算剩下数据的基尼系数。
       ①计算左子树整体数据的基尼系数：因为有5人，其中4人拥有爱情，1人没有拥有爱情，所以p(k) = 4/5。所以求解如下，此系数为树中该分支根节点的gini==0.32。所以左右子树的基尼系数均为0.32。

       ②求特征A1的基尼系数：原理同上。

       ②求特征A2的基尼系数：原理同上。

       ②求特征A4的基尼系数：原理同上。

       综上，Gini(D,A4=1,2)=0.2 最小，所以选择特征A4为最优特征，A4=1=extroversion为最优切分点（即子树根节点）。由于Gini(A4=1)=0,所以该子节点为纯叶子节点。另一节点继续使用上述方法求基尼系数。下面为两个结点的数据：

# 纯叶子结点
RID	 age	    income	handsome	 character	    love
 5	senior	     low	   yes	    extroversion	 yes
 9	youth	     low	   yes	    extroversion	 yes
 10	senior	    medium	   yes	    extroversion	 yes

RID	 age	    income	handsome	 character	    love
 6	senior	     low	   yes	    introvert	     no
 11	youth	    medium	   yes	    introvert	     yes

       第四步：计算剩下数据的基尼系数。
       ①计算左子树整体数据的基尼系数：该分支根节点的基尼系数为：
             gini=2*（1/2）*（1-1/2）=0.5。
       ②求特征A1的基尼系数：原理同上。

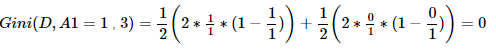
       ②求特征A2的基尼系数：原理同上。

       综上，。由于Gini(A1,A2)=0,所以两个子节点为纯叶子节点。至此左子树分类完毕。右子树的分类跟左子树一样，这里就不再详细写出了。最终结果如下：