机器学习经典算法决策树原理详解（简单易懂）

↑ 点击上方【计算机视觉联盟】关注我们

最经典的决策树算法有ID3、C4.5、CART，其中ID3算法是最早被提出的，它可以处理离散属性样本的分类，C4.5和CART算法则可以处理更加复杂的分类问题，本文重点介绍ID3算法。

1、决策树基本流程

决策树 (decision tree) 是一类常见的机器学习方法。它是对给定的数据集学到一个模型对新示例进行分类的过程。下图所示为一个流程图的决策树，长方形代表判断模块（decision block），椭圆形代表终止模块（terminating block），表示已经得出结论，可以终止运行。从判断模块引出的左右箭头称作分支（branch），可以达到另一个判断模块或终止模块。

决策过程是基于树结构来进行决策的。如下图，首先检查邮件域名地址，如果地址为myEmployer.com，则将其分类为“无聊时需要阅读的邮件”。否则，则检查邮件内容里是否包含单词“曲棍球”，如果包含则归类为“需要及时处理的朋友邮件”，如果不包含则归类到“无需阅读的垃圾邮件”

流程图形式的决策树

显然，决策过程的最终结论对应了我们所希望的判定结果，例如"需要阅读"或"不需要阅读”。

决策过程中提出的每个判定问题都是对某个属性的"测试"，如邮件地址域名为？是否包含“曲棍球”？

每个测试的结果或是导出最终结论，或是导出进一步的判定问题，其考虑范围是在上次决策结果的限定范围之内，例如若邮件地址域名不是myEmployer.com之后再判断是否包含“曲棍球”。

一般的，决策树包含一个根节点、若干个内部节点和若干个叶节点。根节点包含样本全集；叶节点对应于决策结果，例如“无聊时需要阅读的邮件”。其他每个结点则对应于一个属性测试；每个节点包含的样本集合根据属性测试的结果被划分到子结点中。

决策树学习基本算法

显然，决策树的生成是一个递归过程.在决策树基本算法中，有三种情形会导致递归返回: (1)当前结点包含的样本全属于同一类别，无需划分; (2)当前属性集为空，或是所有样本在所有属性上取值相同，无法划分; (3)当前结点包含的样本集合为空，不能划分。

2、划分选择

决策树算法的关键是如何选择最优划分属性。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的"纯度" (purity)越来越高。

（1）信息增益

信息熵

"信息熵" (information entropy)是度量样本集合纯度最常用的一种指标，定义为信息的期望。假定当前样本集合 D 中第 k 类样本所占的比例为

 ,则 D 的信息熵定义为：

                                                                             
H(D)的值越小，则D的纯度越高。信息增益

                                                                 
一般而言，信息增益越大，则意味着使周属性 来进行划分所获得的"纯度提升"越大。因此，我们可用信息增益来进行决策树的划分属性选择，信息增益越大，属性划分越好。

---

以西瓜书中表 4.1 中的西瓜数据集 2.0 为例，该数据集包含17个训练样例，用以学习一棵能预测设剖开的是不是好瓜的决策树.显然，。

在决策树学习开始时，根结点包含 D 中的所有样例，其中正例占 ，反例占 

信息熵计算为：

我们要计算出当前属性集合{色泽，根蒂，敲声，纹理，脐部，触感}中每个属性的信息增益。以属性"色泽"为例，它有 3 个可能的取值: {青绿，乌黑，浅自}。若使用该属性对 D 进行划分，则可得到 3 个子集，分别记为：D1 (色泽=青绿)， D2 (色泽2=乌黑)， D3 (色泽=浅白)。

子集 D1 包含编号为 {1，4，6，10，13，17} 的 6 个样例，其中正例占 p1=3/6 ，反例占p2=3/6； 

D2 包含编号为 {2，3，7，8， 9，15} 的 6 个样例，其中正例占 p1=4/6 ，反例占p2=2/6； 

D3 包含编号为 {5，11，12，14，16} 的 5 个样例，其中正例占 p1=1/5 ，反例占p2=4/5；

根据信息熵公式可以计算出用“色泽”划分之后所获得的3个分支点的信息熵为：

                                                            

根据信息增益公式计算出属性“色泽”的信息增益为（Ent表示信息熵）：

类似的，可以计算出其他属性的信息增益：

显然，属性"纹理"的信息增益最大，于是它被选为划分属性。图 4.3 给出了基于"纹理"对根结点进行划分的结果，各分支结点所包含的样例子集显示在结点中。

然后，决策树学习算法将对每个分支结点做进一步划分。以图 4.3 中第一个分支结点( "纹理=清晰" )为例，该结点包含的样例集合 D 1 中有编号为 {1, 2, 3, 4, 5, 6, 8, 10, 15} 的 9 个样例，可用属性集合为{色泽，根蒂，敲声，脐部 ，触感}。基于 D1计算出各属性的信息增益：

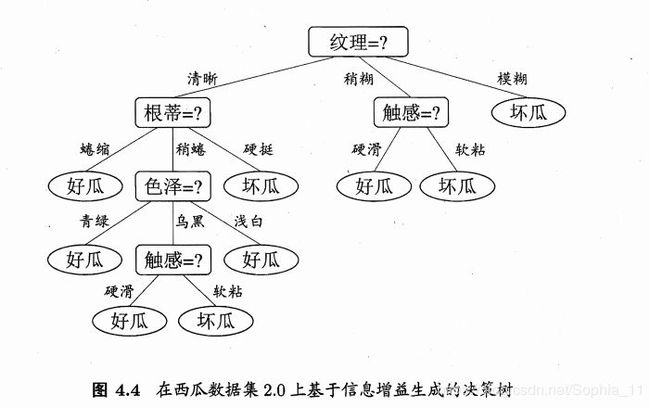
"根蒂"、 "脐部"、 "触感" 3 个属性均取得了最大的信息增益，可任选其中之一作为划分属性.类似的，对每个分支结点进行上述操作，最终得到的决策树如圈 4.4 所示。

3、剪枝处理

剪枝 (pruning)是决策树学习算法对付"过拟合"的主要手段。决策树剪枝的基本策略有"预剪枝" (prepruning)和"后剪枝 "(post"
pruning) [Quinlan, 1993]。

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划
分并将当前结点标记为叶结点；

后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

往期回顾

● 带你详细了解机器视觉竞赛—ILSVRC竞赛

● 到底什么是“机器学习”？机器学习有哪些基本概念？（简单易懂）

● 带你自学Python系列（一）：变量和简单数据类型（附思维导图）

● 带你自学Python系列（二）：Python列表总结-思维导图

● 2018年度最强的30个机器学习项目！

● 斯坦福李飞飞高徒Johnson博士论文: 组成式计算机视觉智能（附195页PDF）

● 一文详解计算机视觉的广泛应用：网络压缩、视觉问答、可视化、风格迁移