常见不等式考察(一)——Jensen不等式
- 常见不等式考察(一)——Jensen不等式
- 0. 引言
- 1. Jensen不等式定义
- 2. Jensen不等式证明
- 3. Jensen不等式的常见形式
- 1. 具体凸函数下的Jesen不等式
- 1. 幂函数
- 2. 对数函数
- 3. 指数函数
- 4. 三角函数
- 2. 连续形式下的Jensen不等式
- 3. 概率论中的Jensen不等式
- 1. 具体凸函数下的Jesen不等式
- 4. 参考链接
0. 引言
这两天在看文献的时候,突然注意到文献中使用了Jensen不等式,然后猛地发现似乎太久不看这些东西,都已经忘得差不多了,是时候得好好复习一下这些东西了……
1. Jensen不等式定义
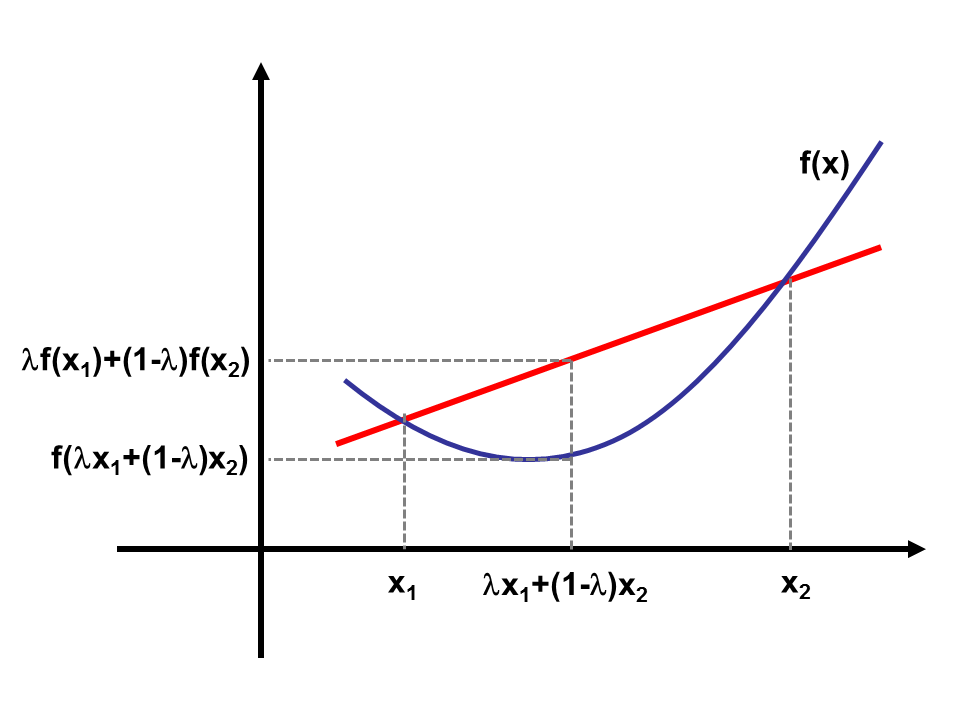
Jensen不等式是针对凸函数的一个常用的不等式,其定义如下:
f ( λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ) ≤ λ ⋅ f ( x 1 ) + ( 1 − λ ) ⋅ f ( x 2 ) f(\lambda \cdot x_1 + (1-\lambda)\cdot x_2) \leq \lambda \cdot f(x_1) + (1-\lambda)\cdot f(x_2) f(λ⋅x1+(1−λ)⋅x2)≤λ⋅f(x1)+(1−λ)⋅f(x2)
上述不等式可以由凸函数的定义快速地得到,我们可以将其推广至一般的情况,即下述表达式:
f ( ∑ i = 1 n λ i x i ) ≤ ∑ i = 1 n λ i f ( x i ) f(\sum_{i=1}^{n} \lambda_i x_i) \leq \sum_{i=1}^{n} \lambda_i f(x_i) f(i=1∑nλixi)≤i=1∑nλif(xi)
其中, ∑ i = 1 n λ i = 1 \sum_{i=1}^{n} \lambda_i = 1 ∑i=1nλi=1。
而如果函数为严格的凹函数,则上述Jensen不等式同样可以成立,但是符号需要反向,即修改为:
f ( ∑ i = 1 n λ i x i ) ≥ ∑ i = 1 n λ i f ( x i ) f(\sum_{i=1}^{n} \lambda_i x_i) \geq \sum_{i=1}^{n} \lambda_i f(x_i) f(i=1∑nλixi)≥i=1∑nλif(xi)
2. Jensen不等式证明
关于Jensen不等式的证明方法,其实网上已经有了不少的解答,不过基本都是基于数学归纳法的解答。
这里,我们来仿照网上的一些解法来自行进行一下推导。
显然,对于 n ≤ 2 n \leq 2 n≤2的情况,又凸函数的定义,上述不等式是易得的。
下面,我们假设在 n = k n=k n=k的情况下,不等式成立,则我们考虑 n = k + 1 n = k+1 n=k+1时的情况。
f ( ∑ i = 1 k + 1 λ i ⋅ x i ) = f ( ∑ i = 1 k λ i ⋅ x i + λ k + 1 ⋅ x k + 1 ) = f ( ( 1 − λ k + 1 ) ⋅ ( ∑ i = 1 k λ i 1 − λ k + 1 ⋅ x i ) + λ k + 1 ⋅ x k + 1 ) ≤ ( 1 − λ k + 1 ) ⋅ f ( ∑ i = 1 k λ i 1 − λ k + 1 ⋅ x i ) + λ k + 1 ⋅ f ( x k + 1 ) ≤ ( 1 − λ k + 1 ) ⋅ ( ∑ i = 1 k λ i 1 − λ k + 1 ⋅ f ( x i ) ) + λ k + 1 ⋅ f ( x k + 1 ) = ∑ i = 1 k λ i ⋅ f ( x i ) + λ k + 1 ⋅ f ( x k + 1 ) = ∑ i = 1 k + 1 λ i ⋅ f ( x i ) \begin{aligned} f(\sum_{i=1}^{k+1} \lambda_i \cdot x_i) & = f(\sum_{i=1}^{k} \lambda_i \cdot x_i + \lambda_{k+1} \cdot x_{k+1}) \\ & = f((1-\lambda_{k+1})\cdot (\sum_{i=1}^{k} \frac{\lambda_i}{1-\lambda_{k+1}} \cdot x_i) + \lambda_{k+1} \cdot x_{k+1}) \\ & \leq (1-\lambda_{k+1})\cdot f(\sum_{i=1}^{k}\frac{\lambda_i}{1-\lambda_{k+1}} \cdot x_i) + \lambda_{k+1} \cdot f(x_{k+1}) \\ & \leq (1-\lambda_{k+1}) \cdot (\sum_{i=1}^{k}\frac{\lambda_i}{1-\lambda_{k+1}} \cdot f(x_i)) + \lambda_{k+1} \cdot f(x_{k+1}) \\ & = \sum_{i=1}^{k} \lambda_i \cdot f(x_i) + \lambda_{k+1} \cdot f(x_{k+1}) \\ & = \sum_{i=1}^{k+1} \lambda_i \cdot f(x_i) \end{aligned} f(i=1∑k+1λi⋅xi)=f(i=1∑kλi⋅xi+λk+1⋅xk+1)=f((1−λk+1)⋅(i=1∑k1−λk+1λi⋅xi)+λk+1⋅xk+1)≤(1−λk+1)⋅f(i=1∑k1−λk+1λi⋅xi)+λk+1⋅f(xk+1)≤(1−λk+1)⋅(i=1∑k1−λk+1λi⋅f(xi))+λk+1⋅f(xk+1)=i=1∑kλi⋅f(xi)+λk+1⋅f(xk+1)=i=1∑k+1λi⋅f(xi)
由此可见,不等式成立。
综上,一般情况下的Jensen不等式即可证明完毕。
而同理,对于凹函数情况下的Jensen不等式,我们只需要完全仿照上述的解法即可证明。
3. Jensen不等式的常见形式
下面,我们来看一下Jensen不等式在不同场景下的一些引申表达方式以及应用。
1. 具体凸函数下的Jesen不等式
1. 幂函数
对于幂函数 f ( x ) = x k f(x) = x^k f(x)=xk,我们有:
( ∑ i = 1 n λ i ⋅ x i ) k ≤ ∑ i = 1 n λ i ⋅ x i k (\sum_{i=1}^{n} \lambda_i \cdot x_i)^k \leq \sum_{i=1}^{n}\lambda_i \cdot x_i^k (i=1∑nλi⋅xi)k≤i=1∑nλi⋅xik
特别的,当所有的系数都相同时,我们即有:
( ∑ i = 1 n x i n ) k ≤ ∑ i = 1 n x i k n (\frac{\sum_{i=1}^{n} x_i}{n})^k \leq \frac{\sum_{i=1}^{n}x_i^k}{n} (n∑i=1nxi)k≤n∑i=1nxik
2. 对数函数
对于对数函数,我们可以写出对应的Jensen不等式如下:
l o g ( ∑ i = 1 n λ i ⋅ x i ) ≤ ∑ i = 1 n λ i ⋅ l o g ( x i ) log(\sum_{i=1}^{n} \lambda_i \cdot x_i) \leq \sum_{i=1}^{n} \lambda_i \cdot log(x_i) log(i=1∑nλi⋅xi)≤i=1∑nλi⋅log(xi)
特别地,当所有的系数都相同时,即有:
l o g ( ∑ i = 1 n x i n ) ≤ 1 n ⋅ ∑ i = 1 n l o g ( x i ) log(\frac{\sum_{i=1}^{n}x_i}{n}) \leq \frac{1}{n} \cdot \sum_{i=1}^{n} log(x_i) log(n∑i=1nxi)≤n1⋅i=1∑nlog(xi)
3. 指数函数
对于指数函数,我们可以写出对应的Jensen不等式如下:
e x p ( ∑ i = 1 n λ i ⋅ x i ) ≤ ∑ i = 1 n λ i ⋅ e x i exp(\sum_{i=1}^{n} \lambda_i \cdot x_i) \leq \sum_{i=1}^{n} \lambda_i \cdot e^{x_i} exp(i=1∑nλi⋅xi)≤i=1∑nλi⋅exi
特别地,当所有的系数都相同时,即有:
e x p ( ∑ i = 1 n x i n ) ≤ 1 n ⋅ ∑ i = 1 n e x i exp(\frac{\sum_{i=1}^{n}x_i}{n}) \leq \frac{1}{n} \cdot \sum_{i=1}^{n} e^{x_i} exp(n∑i=1nxi)≤n1⋅i=1∑nexi
4. 三角函数
对于三角函数(我们以 s i n sin sin为例,其在 [ 0 , π ] [0, \pi] [0,π]范围内为凹函数),我们可以写出对应的Jensen不等式如下:
s i n ( ∑ i = 1 n λ i ⋅ θ i ) ≥ ∑ i = 1 n λ i ⋅ s i n θ i sin(\sum_{i=1}^{n} \lambda_i \cdot \theta_i) \geq \sum_{i=1}^{n} \lambda_i \cdot sin\theta_i sin(i=1∑nλi⋅θi)≥i=1∑nλi⋅sinθi
特别地,当所有的系数都相同时,即有:
s i n ( ∑ i = 1 n θ i n ) ≥ 1 n ⋅ ∑ i = 1 n s i n θ i sin(\frac{\sum_{i=1}^{n}\theta_i}{n}) \geq \frac{1}{n} \cdot \sum_{i=1}^{n} sin\theta_i sin(n∑i=1nθi)≥n1⋅i=1∑nsinθi
特别的,对于三角形的三个内角,我们有:
1 3 ( s i n A + s i n B + s i n C ) ≤ s i n ( π 3 ) \frac{1}{3}(sinA + sinB + sinC) \leq sin(\frac{\pi}{3}) 31(sinA+sinB+sinC)≤sin(3π)
即:
s i n A + s i n B + s i n C ≤ 3 3 2 sinA + sinB + sinC \leq \frac{3\sqrt{3}}{2} sinA+sinB+sinC≤233
2. 连续形式下的Jensen不等式
已知 g ( x ) > 0 g(x) > 0 g(x)>0, ∫ x g ( x ) d x = 1 \int_{x}g(x)dx = 1 ∫xg(x)dx=1,且函数 f ( x ) f(x) f(x)为凸函数,则有:
f ( ∫ x g ( x ) ⋅ x d x ) ≤ ∫ x g ( x ) ⋅ f ( x ) d x f(\int_x g(x) \cdot x dx) \leq \int_x g(x) \cdot f(x) dx f(∫xg(x)⋅xdx)≤∫xg(x)⋅f(x)dx
3. 概率论中的Jensen不等式
特别的,我们将上述2中的连续形式下的 g ( x ) g(x) g(x)函数表示为概率分布函数,那么我们就可以很简单地导出概率论当中常见的Jensen不等式的表达式:
f ( E ˉ ( x ) ) ≤ E ˉ ( f ( x ) ) f(\bar{E}(x)) \leq \bar{E}(f(x)) f(Eˉ(x))≤Eˉ(f(x))
4. 参考链接
- https://en.wikipedia.org/wiki/Jensen%27s_inequality
- https://zhuanlan.zhihu.com/p/39315786
- https://zhuanlan.zhihu.com/p/279442299