融合随机反向学习的黏菌与算术混合优化算法
文章目录
- 一、理论基础
-
- 1、黏菌算法
- 2、算术优化算法
- 3、随机反向学习策略
- 4、融合随机反向学习的黏菌与算术混合优化算法
-
- (1)改进混合算法理论分析
- (2)HSMAAOA伪代码
- 二、实验仿真与分析
- 三、参考文献
一、理论基础
1、黏菌算法
请参考这里。
2、算术优化算法
请参考这里。
3、随机反向学习策略
反向学习策略(Opposition-based Learning, OBL)是Tizhoosh H R等人于2005年提出的群智能领域中的一种改进策略,其思想是:在种群寻优的过程中,根据当前解产生一个反向解,比较当前解与反向解的目标函数值,择优进入下一次迭代。
反向解定义:存在 n n n维坐标系内一点 X X X,同时满足 X ∈ [ L B , U B ] X\in[LB,UB] X∈[LB,UB],则反向解计算公式如下: X ~ = L B + U B − X (1) \widetilde X=LB+UB-X\tag{1} X =LB+UB−X(1)其中, X X X为当前解, X ~ \widetilde X X 为反向解。
由于反向学习策略生成的反向解与当前解距离为一定值,缺乏随机性,无法有效增强搜索空间内种群多样性。因此,Long W等人提出了改进的随机反向学习策略(Random Opposition-based Learning, ROBL),进一步增强种群多样性,提高种群避免局部最优的能力,计算公式如下: X r a n d = L B + U B − r × X (2) X_{rand}=LB+UB-r×X\tag{2} Xrand=LB+UB−r×X(2)其中, X r a n d X_{rand} Xrand表示随机反向解, r r r表示0到1之间的随机数。
4、融合随机反向学习的黏菌与算术混合优化算法
(1)改进混合算法理论分析
本文将SMA和AOA进行了有机融合,提出一种新的混合算法(HSMAAOA)。混合算法分别保留了SMA与AOA的优势特性,首先保留了SMA根据 z z z值进行随机初始化的部分,当 r a n d < z rand
(2)HSMAAOA伪代码
begin
设置种群数量 N,当前迭代 t,最大迭代次数 T,惯性权重 w,
初始化种群位置
while t ≤ T
计算适应度值,幵选出最佳个体与最差个体
通过式(4)更新惯性权重W
for i = 1 to N
if rand < z
通过式(6)计算种群位置
else
更新参数 vb,vc,p
if r1 < p
通过式(6)计算种群位置
else
if r4 < 0.5
通过式(8)计算种群位置
else
通过式(8)计算种群位置
end if
end if
end if
通过式(12)生成随机反向解
end for
end while
end
注:公式编号以文献[1]为准。
二、实验仿真与分析
为了更好的验证HSMAAOA算法性能,选取了7种算法进行对比:SMA、AOA、HHO、WOA、SSA、GWO和PSO,这些算法被证实具有良好的寻优性能。为了更准确的验证所提算法与对比算法的优劣性,设定种群规模 N = 30 N=30 N=30,维度 D = 30 D=30 D=30,最大迭代次数500次,各算法独立运行30次,各算法参数设置如表1所示。选取最优值、最差值、平均值与标准差作为评价指标。其中,平均值与标准差越小,则证明算法的性能越佳。以F1、F3、F5(单峰函数)、F8、F10、F12(多峰函数)、F15、F20、F23(固定维多峰函数)为例。
结果显示如下:
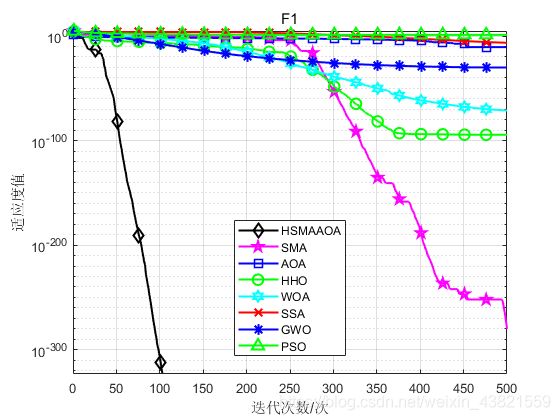
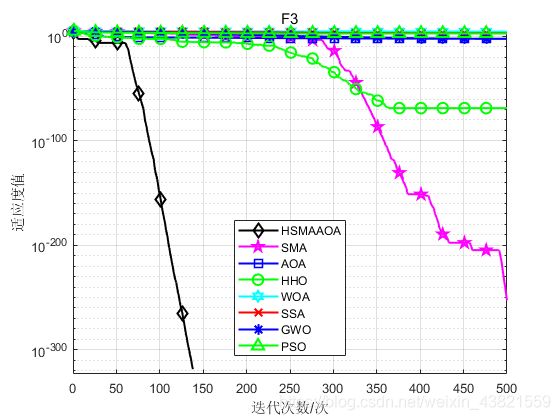
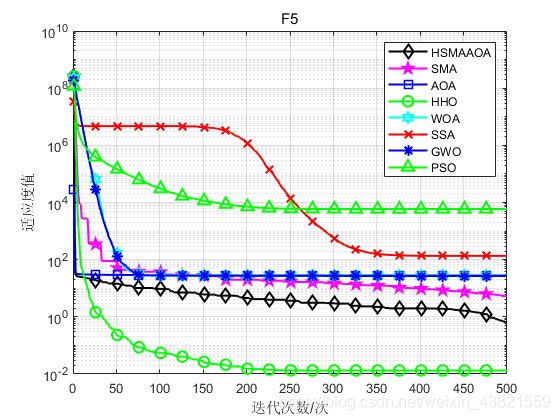
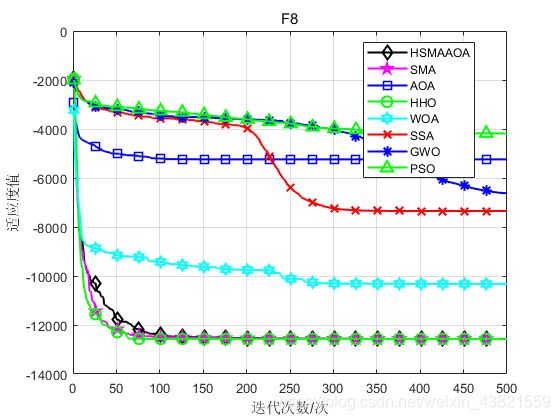


函数:F1
HSMAAOA:Best: 0,Worst:0,Mean:0,Sstd:0
SMA:Best: 0,Worst:2.2963e-279,Mean:7.6543e-281,Std:0
AOA:Best: 1.4098e-155,Worst:7.6368e-10,Mean:2.5456e-11,Std:1.3943e-10
HHO:Best: 7.4441e-114,Wworst:9.5091e-94,Mean:3.391e-95,Std:1.736e-94
WOA:Best: 7.8606e-85,Worst:1.6945e-70,Mean:6.3586e-72,Std:3.0957e-71
SSA:Best: 3.9325e-08,Worst:5.8885e-06,Mean:4.0201e-07,Std:1.0721e-06
GWO:Best: 4.2705e-32,Worst:6.9072e-30,Mean:8.2783e-31,Std:1.2886e-30
PSO:Best: 5.1581,Worst:30.9431,Mean:13.7722,Std:6.6556
函数:F3
HSMAAOA:Best: 0,Worst:0,Mean:0,Sstd:0
SMA:Best: 0,Worst:4.9289e-252,Mean:1.643e-253,Std:0
AOA:Best: 1.3391e-156,Worst:0.10241,Mean:0.0061081,Std:0.018905
HHO:Best: 3.0666e-102,Wworst:6.3294e-68,Mean:2.1098e-69,Std:1.1556e-68
WOA:Best: 7004.6082,Worst:96128.0163,Mean:42140.6983,Std:16188.1162
SSA:Best: 608.2613,Worst:4087.8833,Mean:1622.4263,Std:758.2963
GWO:Best: 1.2157e-05,Worst:0.013967,Mean:0.0039141,Std:0.0040391
PSO:Best: 284.9097,Worst:1187.5016,Mean:626.4399,Std:240.3469
函数:F5
HSMAAOA:Best: 7.5384e-05,Worst:4.9788,Mean:0.65072,Sstd:1.1218
SMA:Best: 2.9934e-05,Worst:28.2203,Mean:5.2242,Std:9.1322
AOA:Best: 27.7426,Worst:28.8821,Mean:28.4267,Std:0.29386
HHO:Best: 8.6167e-05,Wworst:0.077912,Mean:0.013287,Std:0.01961
WOA:Best: 27.101,Worst:28.747,Mean:27.9974,Std:0.46864
SSA:Best: 25.0583,Worst:1139.4475,Mean:135.1859,Std:206.4895
GWO:Best: 25.2859,Worst:28.7464,Mean:26.7416,Std:0.85842
PSO:Best: 1013.9033,Worst:16363.2089,Mean:5912.7981,Std:4145.8487
函数:F8
HSMAAOA:Best: -12569.4866,Worst:-12567.1934,Mean:-12568.9796,Sstd:0.50003
SMA:Best: -12569.4808,Worst:-12568.1345,Mean:-12569.026,Std:0.35531
AOA:Best: -5834.0816,Worst:-4116.1113,Mean:-5241.4154,Std:418.954
HHO:Best: -12569.4866,Wworst:-12564.0806,Mean:-12568.6021,Std:1.3512
WOA:Best: -12569.0294,Worst:-7074.324,Mean:-10322.405,Std:1934.9
SSA:Best: -9120.6839,Worst:-6408.793,Mean:-7349.3604,Std:608.7949
GWO:Best: -8545.6349,Worst:-3461.5389,Mean:-6618.896,Std:1020.6164
PSO:Best: -6873.7787,Worst:-2451.1958,Mean:-4191.9275,Std:1146.4286
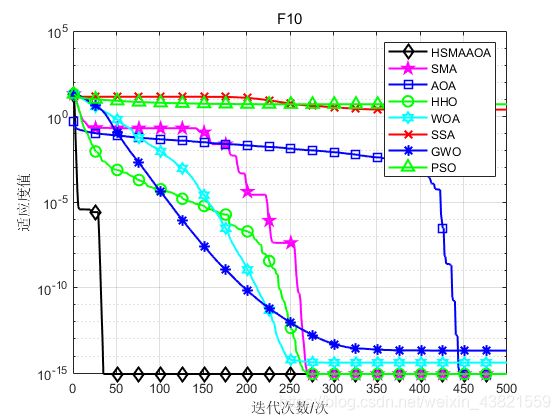
函数:F10
HSMAAOA:Best: 8.8818e-16,Worst:8.8818e-16,Mean:8.8818e-16,Sstd:0
SMA:Best: 8.8818e-16,Worst:8.8818e-16,Mean:8.8818e-16,Std:0
AOA:Best: 8.8818e-16,Worst:8.8818e-16,Mean:8.8818e-16,Std:0
HHO:Best: 8.8818e-16,Wworst:8.8818e-16,Mean:8.8818e-16,Std:0
WOA:Best: 8.8818e-16,Worst:1.5099e-14,Mean:4.0856e-15,Std:3.4089e-15
SSA:Best: 0.93131,Worst:5.1911,Mean:2.5316,Std:0.93001
GWO:Best: 1.5099e-14,Worst:3.2863e-14,Mean:2.0547e-14,Std:4.7329e-15
PSO:Best: 3.2357,Worst:9.7123,Mean:5.192,Std:1.1135
函数:F12
HSMAAOA:Best: 2.4347e-06,Worst:0.0018692,Mean:0.00030965,Sstd:0.00043041
SMA:Best: 1.0492e-07,Worst:0.019239,Mean:0.0039044,Std:0.0051534
AOA:Best: 0.41642,Worst:0.6184,Mean:0.51479,Std:0.053189
HHO:Best: 6.1933e-10,Wworst:6.0642e-05,Mean:1.1308e-05,Std:1.3228e-05
WOA:Best: 0.0043452,Worst:0.26417,Mean:0.030178,Std:0.047226
SSA:Best: 1.2219,Worst:22.2816,Mean:6.7718,Std:3.826
GWO:Best: 0.0022687,Worst:0.13562,Mean:0.021335,Std:0.023772
PSO:Best: 2.5587,Worst:22.262,Mean:8.7699,Std:5.1677
函数:F15
HSMAAOA:Best: 0.00030864,Worst:0.00091102,Mean:0.00047935,Sstd:0.00016528
SMA:Best: 0.00031548,Worst:0.0012255,Mean:0.0005803,Std:0.00027413
AOA:Best: 0.00036261,Worst:0.12146,Mean:0.010216,Std:0.022956
HHO:Best: 0.00030776,Wworst:0.0015524,Mean:0.00037447,Std:0.00022313
WOA:Best: 0.00030751,Worst:0.012678,Mean:0.001223,Std:0.0022351
SSA:Best: 0.0005001,Worst:0.020386,Mean:0.0022074,Std:0.004944
GWO:Best: 0.00030749,Worst:0.020363,Mean:0.0024329,Std:0.0060814
PSO:Best: 0.00030749,Worst:0.022553,Mean:0.0044073,Std:0.0070722
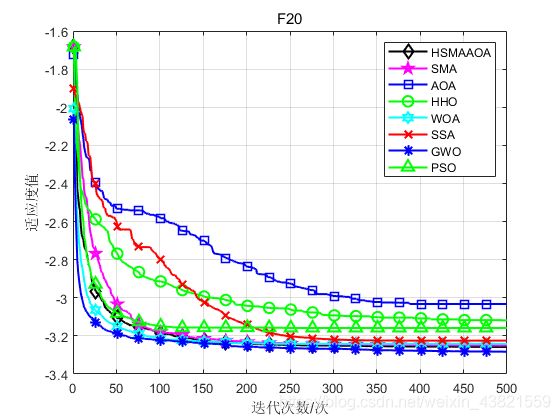
函数:F20
HSMAAOA:Best: -3.322,Worst:-3.2029,Mean:-3.2585,Sstd:0.060346
SMA:Best: -3.322,Worst:-3.201,Mean:-3.2504,Std:0.059451
AOA:Best: -3.2408,Worst:-2.7847,Mean:-3.0328,Std:0.10788
HHO:Best: -3.2455,Wworst:-2.8508,Mean:-3.1185,Std:0.098383
WOA:Best: -3.3217,Worst:-2.8402,Mean:-3.2421,Std:0.11475
SSA:Best: -3.322,Worst:-3.1769,Mean:-3.2248,Std:0.054858
GWO:Best: -3.322,Worst:-3.1377,Mean:-3.283,Std:0.061684
PSO:Best: -3.322,Worst:-2.6381,Mean:-3.1586,Std:0.18509
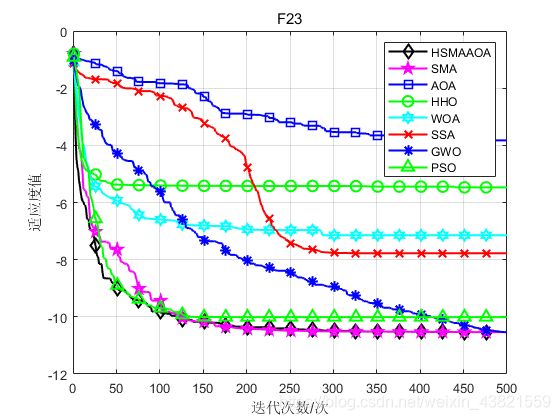
函数:F23
HSMAAOA:Best: -10.5364,Worst:-10.535,Mean:-10.5358,Sstd:0.00037483
SMA:Best: -10.5364,Worst:-10.5345,Mean:-10.536,Std:0.00037111
AOA:Best: -8.4519,Worst:-1.7403,Mean:-3.8275,Std:1.5087
HHO:Best: -10.3676,Wworst:-5.1077,Mean:-5.4701,Std:1.3182
WOA:Best: -10.5363,Worst:-1.6752,Mean:-7.1461,Std:3.345
SSA:Best: -10.5364,Worst:-2.4273,Mean:-7.7749,Std:3.4973
GWO:Best: -10.5364,Worst:-10.5354,Mean:-10.5361,Std:0.00025163
PSO:Best: -10.5364,Worst:-2.4273,Mean:-10.0084,Std:2.0098
结果表明:融合随机反向学习策略的黏菌与算术混合优化算(HSMAAOA)全局与局部能力均得到加强,优于原始SMA、AOA及其他5种优化算法,表现出更优秀的收敛精度、收敛速度以及稳定性。
三、参考文献
[1] 贾鹤鸣, 刘宇翔, 刘庆鑫, 王爽, 郑荣. 融合随机反向学习的黏菌与算术混合优化算法[J]. 计算机科学与探索, 0, (): 1-12.DOI:10.3778/j.issn.1673-9418.2105016.