java 二叉树的相关操作
基本数据结构:
public class TreeNode {
T val;
TreeNode left=null;
TreeNode right=null;
public TreeNode(T val){
this.val=val;
}
//二叉树最大深度
static int maxDeath(TreeNode node){
if(node==null){
return 0;
}
int left = maxDeath(node.left);
int right = maxDeath(node.right);
return Math.max(left,right) + 1;
}
}
一.创建树
0.表达式树
0.1 中缀表达式转为后缀表达式
将中缀表达式转换为后缀表达式:
与转换为前缀表达式相似,遵循以下步骤:
(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;
(2) 从左至右扫描中缀表达式;
(3) 遇到操作数时,将其压入S2;
(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:
(4-1) 如果S1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
(4-2) 否则,若优先级比栈顶运算符的高,也将运算符压入S1(注意转换为前缀表达式时是优先级较高或相同,而这里则不包括相同的情况);
(4-3) 否则,将S1栈顶的运算符弹出并压入到S2中,再次转到(4-1)与S1中新的栈顶运算符相比较;
(5) 遇到括号时:
(5-1) 如果是左括号“(”,则直接压入S1;
(5-2) 如果是右括号“)”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到左括号为止,此时将这一对括号丢弃;
(6) 重复步骤(2)至(5),直到表达式的最右边;
(7) 将S1中剩余的运算符依次弹出并压入S2;
(8) 依次弹出S2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式(转换为前缀表达式时不用逆序)。
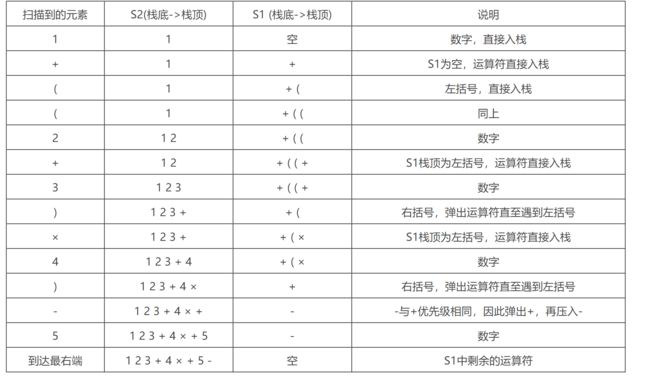
例如,将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程如下:
因此结果为“1 2 3 + 4 × + 5 -”(注意需要逆序输出)。
编写Java程序将一个中缀表达式转换为前缀表达式和后缀表达式,并计算表达式的值。其中的toPolishNotation()方法将中缀表达式转换为前缀表达式(波兰式)、toReversePolishNotation()方法则用于将中缀表达式转换为后缀表达式(逆波兰式):
引用
http://blog.csdn.net/antineutrino/article/details/6763722/
以下是我断断续续写出来的中缀转后缀的代码,不保证没有bug
package Chapter4;
import java.util.Scanner;
import java.util.Stack;
public class TransferExpression {
//中缀表达式a + b*c + (d * e + f) * g,其转换成后缀表达式则为a b c * + d e * f + g * +。
/**
* 思路:
* 一.过程:输入一个String,它是正常的中缀表达式
* 根据toReversePolishNotation方法返回后缀表达式
* 二.步骤:
* 1.初始化两个栈,栈b为输出栈,栈a保存临时运算符
* 2.遍历input
* 2.1.遍历到非操作符时,栈b push()
* 2.2.遍历到运算符 + - * / ( )时
* 2.2.1 优先级 ( ) >> * / >> + - ,
* 2.2.2 遍历到 ( 无条件 栈a push()
* 2.2.3 遍历到 ) 时,栈a pop(),栈b push() 直到pop()== ( 停止pop和push
* 2.2.4 遍历到 * /时,若栈 a.peek() < * / a push(),否则push a.pop to b 直到a 空或没有更大的
* 2.3.输出栈c
* 结束。
* a+b*c+(d*e+f)*g
*/
public static String toReversePolishNotation(String input){
String output="";
Stack stackA=new Stack<>();
Stack stackB=new Stack<>();
for(int i=0;i0){
String compare1=stackA.peek();
if(compare1.equals("*") || compare1.equals("/")){
stackA.pop();
stackB.push(compare1);
}else{
stackA.push(s);
break;
}
}
}
}
if(s.equals("+") || s.equals("-")){
if(stackA.size() == 0){
stackA.push(s);
}else {
while (stackA.size() > 0) {
String compare1 = stackA.peek();
if (!compare1.equals("(")) {
stackA.pop();
stackB.push(compare1);
} else {
break;
}
}
stackA.push(s);
}
if(s.equals("(")){
stackA.push(s);
}
}
}else{
if(s.equals(")")){
if(stackA.size() == 0){
stackA.push(s);
}else {
while (stackA.size() > 0) {
String compare = stackA.pop();
if (compare.equals("(")) {
break;
} else {
stackB.push(compare);
}
}
}
}else{
stackB.push(s);
}
}
}
while(stackA.size()>0){
stackB.push(stackA.pop());
}
while (stackB.size()>0){
output+=stackB.pop();
}
String outputReverse="";
for(int i=output.length()-1;i>-1;i--){
outputReverse+=output.substring(i,i+1);
}
return outputReverse;
}
public static void main(String[] args){
Scanner in=new Scanner(System.in);
String input=in.next();
System.out.println(toReversePolishNotation(input));
}
}
第二种思路:
2.3)转换的另一种方法
1)先按照运算符的优先级对中缀表达式加括号,变成( ( a+(bc) ) + ( ((de)+f) g ) )
2)将运算符移到括号的后面,变成((a(bc))+(((de)f)+g))+
3)去掉括号,得到abc+def+g*+
http://blog.csdn.net/sgbfblog/article/details/8001651
那么后缀表达式如何计算呢
http://blog.csdn.net/yangquanhui1991/article/details/52187375
public static Double sum(String s){
Stack stack=new Stack<>();
for(int i=0;i 二叉树应用——后缀表达式构建表达式树
http://blog.csdn.net/qq_26849233/article/details/72910010
public static void main(String[] args){
Scanner in=new Scanner(System.in);
String input=in.next();
String postFix=toReversePolishNotation(input);
//System.out.println(sum(postFix));
TreeNode treeNode=createTreeNode(postFix,"+-*/");
System.out.println(treeNode);
}
public static TreeNode createTreeNode(String s,String operation){
Stack stack=new Stack<>();
for(int i=0;i 输出树
https://stackoverflow.com/questions/4965335/how-to-print-binary-tree-diagram
计算二叉树的最大深度:
static int maxDeath(TreeNode node){
if(node==null){
return 0;
}
int left = maxDeath(node.left);
int right = maxDeath(node.right);
return Math.max(left,right) + 1;
}
1.根据括号法创建树
1.1通过 A(B(D(#,G)),C(E,F)) 形式创建二叉树
1.2通过 A(B(D(,G)),C(E,F)) 形式创建二叉树
2.通过输入遍历顺序 创建二叉树
//二叉树最大深度
int maxDeath(TreeNode node){
if(node==null){
return 0;
}
int left = maxDeath(node.left);
int right = maxDeath(node.right);
return Math.max(left,right) + 1;
}
以下代码是从中缀表达式到转为后缀表达式到后缀表达式转为二叉树到二叉树输出
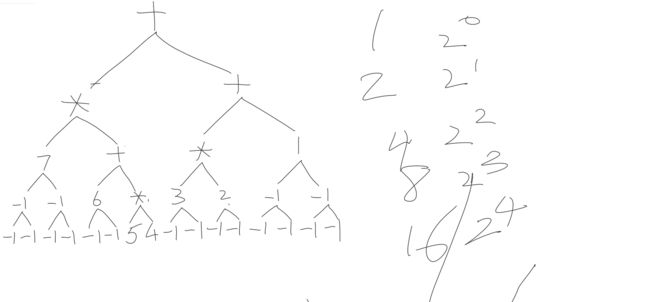
原理图:(我知道很丑)
package Chapter4;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
/**
* Description: 类TreeNode和他的一些方法们
* @author: lsk
* @date :2018-02-39 22:46:35
* @param
*/
public class TreeNode {
T val;
TreeNode left=null;
TreeNode right=null;
public TreeNode(T val){
this.val=val;
}
/**
* Description: 得到node的深度
* @author: lsk
* @date :2018-02-39 22:48:25
* @param node
* @return
*/
static int maxDeath(TreeNode node){
if(node==null){
return 0;
}
int left = maxDeath(node.left);
int right = maxDeath(node.right);
return Math.max(left,right) + 1;
}
/**
* Description:
* @author: lsk
* @date :2018-02-39 22:45:39
* @param s 传入的后缀表达式
* @param operation 操作符
* @return
*/
public static TreeNode createTreeNode(String s,String operation){
Stack stack=new Stack<>();
for(int i=0;i package Chapter4;
import com.sun.org.apache.xpath.internal.operations.Bool;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
import java.util.Stack;
public class TransferExpression {
//中缀表达式a + b*c + (d * e + f) * g,其转换成后缀表达式则为a b c * + d e * f + g * +。
/**
* 思路:
* 一.过程:输入一个String,它是正常的中缀表达式
* 根据toReversePolishNotation方法返回后缀表达式
* 二.步骤:
* 1.初始化两个栈,栈b为输出栈,栈a保存临时运算符
* 2.遍历input
* 2.1.遍历到非操作符时,栈b push()
* 2.2.遍历到运算符 + - * / ( )时
* 2.2.1 优先级 ( ) >> * / >> + - ,
* 2.2.2 遍历到 ( 无条件 栈a push()
* 2.2.3 遍历到 ) 时,栈a pop(),栈b push() 直到pop()== ( 停止pop和push
* 2.2.4 遍历到 * /时,若栈 a.peek() < * / a push(),否则push a.pop to b 直到a 空或没有更大的
* 2.3.输出栈c
* 结束。
* a+b*c+(d*e+f)*g
* 1+2*3+(4*5+6)*7
*/
public static String toReversePolishNotation(String input){
String output="";
Stack stackA=new Stack<>();
Stack stackB=new Stack<>();
for(int i=0;i0){
String compare1=stackA.peek();
if(compare1.equals("*") || compare1.equals("/")){
stackA.pop();
stackB.push(compare1);
}else{
stackA.push(s);
break;
}
}
}
}
if(s.equals("+") || s.equals("-")){
if(stackA.size() == 0){
stackA.push(s);
}else {
while (stackA.size() > 0) {
String compare1 = stackA.peek();
if (!compare1.equals("(")) {
stackA.pop();
stackB.push(compare1);
} else {
break;
}
}
stackA.push(s);
}
if(s.equals("(")){
stackA.push(s);
}
}
}else{
if(s.equals(")")){
if(stackA.size() == 0){
stackA.push(s);
}else {
while (stackA.size() > 0) {
String compare = stackA.pop();
if (compare.equals("(")) {
break;
} else {
stackB.push(compare);
}
}
}
}else{
stackB.push(s);
}
}
}
while(stackA.size()>0){
stackB.push(stackA.pop());
}
while (stackB.size()>0){
output+=stackB.pop();
}
String outputReverse="";
for(int i=output.length()-1;i>-1;i--){
outputReverse+=output.substring(i,i+1);
}
return outputReverse;
}
public static void main(String[] args){
}
}
package Chapter4;
import java.util.ArrayList;
import java.util.List;
/**
* Description: 输出二叉树
* @author: lsk
* @date :2018-02-39 22:52:17
*/
public class PrintTreeNode {
public static void main(String[] args){
//Scanner in=new Scanner(System.in);
//输入中缀表达式
//String input=in.next();
String input="1+2*3+(4*5+6)*7";
TreeNode treeNode=getTreeNode(input,"+-*/");
PrintTree(treeNode);
}
/**
* Description: 得到count个空格
* @author: lsk
* @date :2018-02-39 23:01:14
* @param count
* @return
*/
public static String getBlankSpace(Double count){
String s="";
for(int i=0;i treeNodeList){
for(TreeNode treeNode:treeNodeList){
if(treeNode != null){
return false;
}
}
return true;
}
public static Boolean checkListAllNull(List list,String stopParam){
for(TreeNode treeNode:list){
if(!treeNode.val.equals(stopParam)){
return false;
}
}
return true;
}
/**
* Description: 输出二叉树
* @author: lsk
* @date :2018-02-39 23:05:22
* @param treeNodeList
* @param depth
* @param floor
* @param stopParam
*/
public static void printTreeNode(List treeNodeList,int depth,int floor,String stopParam){
//如果treeNodeList所有值都是stopParam的,则递归结束
if(PrintTreeNode.checkListAllNull(treeNodeList,stopParam)){
return;
}else {
//如果treeNodeList所有值都是空的,则递归结束
if (treeNodeList.isEmpty() || PrintTreeNode.isAllElementsNull(treeNodeList)) {
return;
} else {
List newTreeNodeList = new ArrayList<>();
String blankSpace="";
int count=0;
for (TreeNode treeNode : treeNodeList) {
//list的get(0)的二叉树输出前需要有 2^(depth-floor) 个空格
if(count == 0){
blankSpace=PrintTreeNode.getBlankSpace(Math.pow(2,(depth-floor)));
}else{
//其余二叉树输出前需要 2^(depth-floor+1)-1 个空格
blankSpace=PrintTreeNode.getBlankSpace(Math.pow(2,(depth-floor+1))-1);
}
count++;
//遍历treeNode
if (treeNode != null) {
System.out.print(blankSpace + treeNode.val);
if (treeNode.left != null) {
newTreeNodeList.add(treeNode.left);
} else {
if (!treeNode.val.toString().equals(stopParam)) {
newTreeNodeList.add(TreeNode.createANullTreeNode(stopParam));
}
}
if (treeNode.right != null) {
newTreeNodeList.add(treeNode.right);
} else {
if (!treeNode.val.toString().equals(stopParam)) {
newTreeNodeList.add(TreeNode.createANullTreeNode(stopParam));
}
}
}
}
System.out.println();
printTreeNode(newTreeNodeList, depth, floor + 1,stopParam);
}
}
}
/**
* Description: 通过后缀表达式的String转为TreeNode
* @author: lsk
* @date :2018-02-40 09:49:05
* @param input
* @param operation
* @return
*/
public static TreeNode getTreeNode(String input,String operation){
String postFix=TransferExpression.toReversePolishNotation(input);
//通过后缀表达式转为二叉树
return TreeNode.createTreeNode(postFix,operation);
}
/**
* Description: 输出树
* @author: lsk
* @date :2018-02-40 09:37:14
*/
public static void PrintTree(TreeNode treeNode){
//得到二叉树的深度
int depth=TreeNode.maxDeath(treeNode);
//设定二叉树的位置
int floor=1;
List treeNodeList=new ArrayList<>();
treeNodeList.add(treeNode);
String stopParam=" ";
//输出二叉树
printTreeNode(treeNodeList,depth,floor,stopParam);
}
}
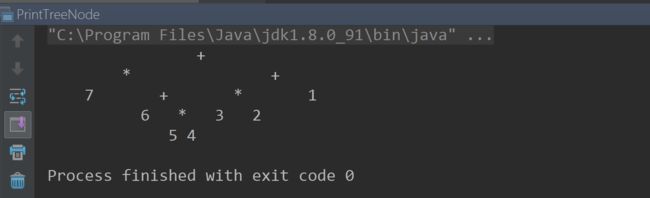
结果: