论文复现——PFLD——人脸关键点检测
PFLD:A Pratical Facial Landmark Detector
论文下载
1. 网络简介
-
人脸关键点检测任务是很多人脸相关任务的基础,比如换脸、人脸变换、人脸识别等等;
-
现实中,人脸通常暴露在复杂环境中,同样的人脸图像可能因为姿势、表情、光线以及遮挡等问题而非常不同。采集同一个人在不同环境不同姿势情况下的数据集理论上可行,但是实际操作很难实现,因为所需的训练数据量太大了。
-
作者总结了人脸关键点问题的四个难点:
- 局部变量影响(Local Variation):表情、局部光照、阴影或遮挡都会使部分关键点发生偏移甚至消失;
- 全局变量影响(Global Variation):人脸姿势和图像质量都会从全局上影响图像中人脸的情况;
- 样本不均衡(Data Imbalance):不同类型的人脸图像,其样本数量的差异很大是很常见的情况。从而导致训练模型在不同情况下的算法精度不太相同
- 模型效率(Model Efficiency):随着手机等便携设备的普及,在真正应用该技术时,通常要求算法在占据内存小的情况下还具有较高的检测效率,这对模型的要求就更高了。
-
传统人脸关键点检测算法有:AAMs(active appearance models),CLMs(Constrained local models),TSPM(tree strcture part model),ESR(explicit shape regression)和SDM(supervised descent method)。这些方法的共同局限性在于对不同环境不够鲁棒,所需计算资源也比较大。
-
作者认为,全局变量影响相比于局部变量更加严重,更值得关注。为了增加算法鲁棒性,作者利用部分网络来预测人脸的几何信息,然后再进行人脸关键点定位。为了避免样本不均衡问题,作者对样本稀少的类型采用了更高的损失权重。因此,结合了几何信息和样本不均衡的情况,作者设计了新的损失函数。
-
为了提升感受野,更好获取人脸的全局信息,作者在网络中应用了multi-scale fully-connected(MS-FC)层,以便提高定位精度。
-
为了精简模型,并提升网络速度,作者采用MobileNet模块作为backbone。
2. 网络结构
2.1 损失函数
假设真实关键点 X : = [ x 1 , . . . , x N ] ∈ R 2 × N X:=[x_1,...,x_N]\in R^{2\times N} X:=[x1,...,xN]∈R2×N,网络预测关键点 Y : = [ y 1 , . . . , y N ] ∈ R 2 × N Y:=[y_1,...,y_N]\in R^{2\times N} Y:=[y1,...,yN]∈R2×N。如果简单的用L2或L1loss作为损失,则代表对于每一对关键点都平等对待,而没有考虑人脸几何/结构信息,这是不合理的。因为考虑到人脸姿态相对于相机的投影问题,图像上不同位置上两个点同样的距离映射回三维空间时,其三维空间的真实距离并不相同。因此,设计损失函数的时候需要把几何信息考虑进去,有利于减缓该情况的影响。
对于人脸图像来说,人脸的3D姿势就足够决定相机的投影方式。因此,我们假定三维关键点信息是 U ∈ R 4 × N U\in R^{4\times N} U∈R4×N,每一列都是一个三维关键点的坐标 [ u i , v i , z i , 1 ] T [u_i,v_i,z_i,1]^T [ui,vi,zi,1]T。因此,很容易知道X和U的投影关系: X = P U X=PU X=PU,其中P是 2 × 4 2\times4 2×4的投影矩阵,有六个自由度(yaw,roll,pitch,scale,x,y)。局部影响因素(比如表情等)几乎不影响投影信息。由于本论文中,人脸图像都被完整检测并中心化和标准化过,所以scale,x和y三个自由度可以忽略,只需要考虑三个欧拉角自由度。
考虑到样本不均衡的问题,对于不同量级的样本,都会有各自的损失权重。因此损失函数数学表达式如下:
L = 1 M ∑ m = 1 M ∑ n = 1 N γ n ∣ ∣ d n m ∣ ∣ L=\frac{1}{M}\sum_{m=1}^M\sum_{n=1}^N \gamma_n||d_n^m|| L=M1m=1∑Mn=1∑Nγn∣∣dnm∣∣
其中, ∣ ∣ d n m ∣ ∣ ||d_n^m|| ∣∣dnm∣∣表示用某种距离度量方式来度量第m个输入的第n个关键点,本文中使用L2距离作为度量方式。N是人为定义的关键点数量,M是样本数量。 γ n \gamma_n γn是损失的权重,其计算方式如下:
γ n = ∑ c = 1 C ω n c ∑ k = 1 K ( 1 − cos θ n k ) L = 1 M ∑ m = 1 M ∑ n = 1 N ( ∑ c = 1 C ω n c ∑ k = 1 K ( 1 − cos θ n k ) ) ∣ ∣ d n m ∣ ∣ 2 2 \gamma_n=\sum_{c=1}^C \omega_n^c\sum_{k=1}^K(1-\cos\theta_n^k) \\ L=\frac{1}{M}\sum_{m=1}^M\sum_{n=1}^N \big( \sum_{c=1}^C \omega_n^c\sum_{k=1}^K(1-\cos\theta_n^k) \big)||d_n^m||^2_2 γn=c=1∑Cωnck=1∑K(1−cosθnk)L=M1m=1∑Mn=1∑N(c=1∑Cωnck=1∑K(1−cosθnk))∣∣dnm∣∣22
其中K=3, θ 1 , θ 2 , θ 3 \theta^1,\theta^2,\theta^3 θ1,θ2,θ3分别代表真实样本和预测样本三个偏转角的差值(0~180°),可见,差值越大,损失权重越大。其中, d n m d_n^m dnm是来自backbone网络,而 θ n k \theta_n^k θnk是来自辅助网络。
此外,我们将人脸图像分为多标签的样本,标签种类分别是:侧脸、正脸、抬头、低头、表情和遮挡,共6类。然后C=6, ω n c \omega_n^c ωnc表示属于c类的权重,简单的根据类别数量的比例设定权重。
其实实际实现上, ω n c \omega_n^c ωnc和 θ n k \theta_n^k θnk和n并无关系,可以将下标n去掉,并不是说同一张图的每个关键点都有一个权重,而是一张图都共用一个权重。
不考虑权重项,上述损失函数就是简单的L2损失,简单的L2损失就可以涵盖局部影响因素所产生的关键点偏差。
相比于前人提出的引入3D姿态信息的损失函数,作者描述自己损失函数的优点如下:
- 将3D和2D的信息整合在一起,相比于直接加入3D信息更合理;
- 前向和反向传播计算都更加简单;
- 让网络是one-stage,有利于后续网络优化;
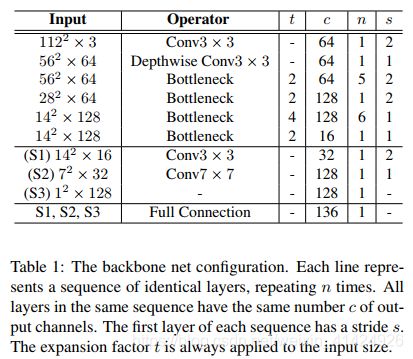
2.2 Backbone网络
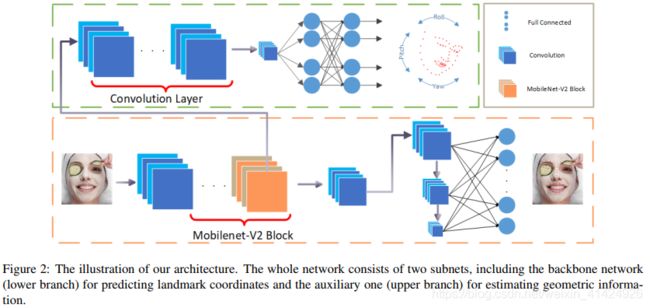
因为人脸具备很强的结构信息,比如对称性、五官的布局等,这些信息有助于让关键点定位更加准确。因此,作者希望采用多尺度特征图,而不是单尺度,来提供更加完整的信息。多尺度是通过调整卷积步长的方式来实现,这可以提高感受野。然后,网络在最后预测时,将多尺度的特征图全连接起来。
作者用简单的backbone来测试自己设计的辅助网络和损失函数确实对人脸关键点问题很有帮助。最终,作者使用MobileNet的深度可分离卷积层和linear inversed residual bottleneck搭建了如下图所示的backbone网络。根据需求可以和MobileNet一样调整backbone网络的超参数,来换取速度和精度的平衡。
2.3 辅助网络
前人研究表明,增加合适的辅助限制可以让人脸关键点检测更稳定更鲁棒。因此作者在本论文中也使用了辅助网络。本论文中的辅助网络负责预测人脸3D姿态的偏转角度信息yaw, pitch, roll。有了这三个偏转角度,人脸的偏转姿态就被确定。
为什么不直接在主网络里预测偏转角,要增加辅助网络?因为关键点在训练初期肯定非常不准,用这些不准的关键点来计算偏转角肯定也非常不准,这两个问题耦合在一起会加大网络训练难度,让训练产生过度惩罚或者无法收敛等问题。为了解耦这层关系,因此作者利用两个网络来分别完成两部分问题。
理论而言,如果有正脸图像,可以计算出偏转姿态的人脸的三个偏转角度。但是并非所有训练图像都有对应的正脸图像。而作者认为他的辅助网络可以不需要正脸图像就输出偏转角度,因为人脸是非常具有结构性的图像,而一张平均的正脸图像基本适用于所有不同的人脸图像,通过对应结构的位置理论上可以直接计算出偏转角度。因此,作者采用如下步骤计算偏转角:
- 预定义一张标准脸(采用多张正脸的平均值),在人脸上固定11个关键点作为所有训练图像的参照标准;
- 利用每张人脸图像对应的11个关键点和上述标准的11个关键点来估算一个旋转矩阵;
- 从旋转矩阵中计算三个偏转角。
尽管上述计算的偏转角可能并不是非常准确,但是作者后续实验证明,这个角度精度已经足够满足本论文所涉及的问题的要求。
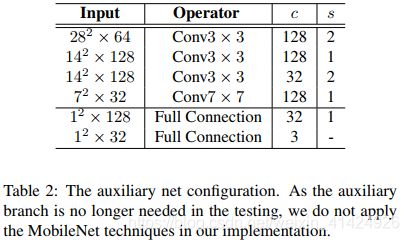
上图是辅助网络的结构,是从backbone网络第4层引出的分支。
2.4 网络细节
作者使用的数据集有两个,一个是300W,另一个是AFLW。300W数据集,3148张作训练集,689张作测试集;AFLW数据集,20000张作训练集,4386张作测试集。
所有输入图像根据人脸bbox,都裁剪并缩放成112x112。作者采用batchsize=256,优化方法采用Adam,weight decay= 1 0 − 6 10^{-6} 10−6,momentum=0.9。最大迭代数量是6.4w次,学习率固定为 1 0 − 4 10^{-4} 10−4。
数据增广部分,对于300W数据集,作者采用了翻转、以5°为间隔旋转图像(-30°~30°)。另外,在人脸区域的20%采用随机的遮挡。对于AFLW数据集,作者不做任何数据增广。
在testing的时候,只使用了backbone网络。
评价指标
作者使用了NME(normalized mean error)和CED(cummulative error distribution)来度量关键点准确性。
3. 论文复现
代码已上传github: https://github.com/lavendelion/my-PFLD-pytorch
3.1 数据集准备
数据集的下载参见github里的README.md。
主要说明一下以下几点:
- 原论文的数据集获取比较繁琐,且论文没有公开他们使用这些数据集的标签。因此github上高星项目,他们复现使用的是WFLW数据集。所以我们也使用该数据集。
- 数据原有7500张训练集,根据论文的数据增广,将数据离线增广为75000张,增广过程在代码"./dataPrepare"里已经完成,只要按步骤使用即可。数据增广很重要,可以很大程度提高最终效果的上限。博主尝试过用无增广的数据进行训练,最终结果鲁棒性差很多。
- WFLW是98个关键点的人脸数据集。
- 数据集准备的难点在于,如何准备论文中提到的欧拉角。根据论文的描述,每张人脸图像应该都对应三个欧拉角,分别表示和标准人脸姿态的三个偏转角度pitch, yaw, roll。该部分可以参见
./dataPrepare/my_prepare_data.py的calculate_pitch_yaw_roll()函数,不详述原理,简单来说就是一个标准三维人脸关键点,通过相机投影关系映射为2D图像坐标的过程。然后在该过程中存在映射矩阵,计算出映射矩阵后可以对应计算出三个旋转角度。 - 关键点坐标都进行了归一化,欧拉角保留角度制,不进行归一化。
- 由于数据集不同,论文中提到的人脸姿态的6类多标签在WFLW中也有所不同,变为:姿态、表情、照度、化妆、遮挡和模糊六种表情。
- 注意一下处理数据的顺序,因为获取欧拉角需要原图像的关键点标注,而如果图像进行翻转、旋转等增广后,关键点数据就会改变。所以要先对图像进行翻转、旋转等增广,同时改变图像的关键点坐标,然后再用最终的关键点坐标计算三个欧拉角。
3.2 训练网络
1). 损失函数
解释一下实际使用时,损失函数的含义,有助于理解损失函数的代码实现:
L = 1 M ∑ m = 1 M ∑ n = 1 N ( ∑ c = 1 C ω n c ∑ k = 1 K ( 1 − cos θ n k ) ) ∣ ∣ d n m ∣ ∣ 2 2 L=\frac{1}{M}\sum_{m=1}^M\sum_{n=1}^N \big( \sum_{c=1}^C \omega_n^c\sum_{k=1}^K(1-\cos\theta_n^k) \big)||d_n^m||^2_2 L=M1m=1∑Mn=1∑N(c=1∑Cωnck=1∑K(1−cosθnk))∣∣dnm∣∣22
-
∣ ∣ d n m ∣ ∣ 2 2 ||d_n^m||^2_2 ∣∣dnm∣∣22:其实就是网络预测的98个关键点坐标和图像对应真实的关键点坐标的L2-distance。
-
θ n k \theta_n^k θnk:是网络辅助分支输出的三个欧拉角和真实图像欧拉角的差值,k=1,2,3。按照2.1节的解释可知,该参数其实和n下标没关系,也就是和具体哪个关键点没关系。所以, ∑ k = 1 K ( 1 − cos θ n k ) \sum_{k=1}^K(1-\cos\theta_n^k) ∑k=1K(1−cosθnk)计算后得到的张量尺寸就是(batchsize, 1)。
-
ω n c \omega_n^c ωnc:该参数也与n下标无关。是在当前训练batch中,第c种属性的权重。比如说,batch=10,具有属性1的数量有2张,那么 ω 1 = 10 / 2 = 5 \omega^1=10/2=5 ω1=10/2=5,这样可以缓解样本不均衡的问题。而对于一张图像,它的 ∑ c = 1 C ω n c \sum_{c=1}^C \omega_n^c ∑c=1Cωnc应该等于 ∑ c = 1 C ω n c I ( a t t r c = = 1 ) \sum_{c=1}^C \omega_n^cI(attr^c==1) ∑c=1CωncI(attrc==1), I ( a t t r c = = 1 ) I(attr^c==1) I(attrc==1)表示这张图像是否包含该属性。也就是说,如果该图像不含有该属性,则无论权重是多少都不需要加上该属性。反之则需要。
所以其实实际使用时,损失函数由三部分组成:人脸姿态属性权重 × 欧拉角权重 × 关键点的L2distance。
2). 网络结构
网络结构部分,论文都说的挺清楚了,需要说明的是,在主网络中,S1,S2层的输出后都需要增加一个全局池化,将张量从14x14, 7x7转换为1x1的尺寸,以便后续和S3的结果进行叠加后,输入全连接层。
3). 训练过程
评价指标metric简单采用不含权重的关键点L2-distance。
训练过程的信息会保存在./checkpoints/log.txt中,比如:
2021-02-14 22:38:35
training epoch 1
Epoch 1/200 | Iter 0/703 | training loss = 278.343, avg_loss = 278.343 | metric = 63.03, avg_metric = 63.03
Epoch 1/200 | Iter 100/703 | training loss = 48.294, avg_loss = 120.505 | metric = 28.99, avg_metric = 42.15
Epoch 1/200 | Iter 200/703 | training loss = 17.584, avg_loss = 74.714 | metric = 15.74, avg_metric = 31.87
Epoch 1/200 | Iter 300/703 | training loss = 9.706, avg_loss = 54.160 | metric = 8.64, avg_metric = 25.17
Epoch 1/200 | Iter 400/703 | training loss = 4.585, avg_loss = 42.309 | metric = 4.87, avg_metric = 20.52
Epoch 1/200 | Iter 500/703 | training loss = 3.485, avg_loss = 34.720 | metric = 3.34, avg_metric = 17.26
Epoch 1/200 | Iter 600/703 | training loss = 2.163, avg_loss = 29.469 | metric = 2.81, avg_metric = 14.90
Epoch 1/200 | Iter 700/703 | training loss = 2.564, avg_loss = 25.659 | metric = 2.67, avg_metric = 13.16
Training consumes 292.32 second
…
2021-02-14 22:58:09
training epoch 5
Epoch 5/200 | Iter 0/703 | training loss = 0.817, avg_loss = 0.817 | metric = 0.99, avg_metric = 0.99
Epoch 5/200 | Iter 100/703 | training loss = 0.818, avg_loss = 0.897 | metric = 0.96, avg_metric = 1.04
Epoch 5/200 | Iter 200/703 | training loss = 0.793, avg_loss = 0.890 | metric = 0.90, avg_metric = 1.02
Epoch 5/200 | Iter 300/703 | training loss = 0.565, avg_loss = 0.861 | metric = 0.88, avg_metric = 1.00
Epoch 5/200 | Iter 400/703 | training loss = 0.486, avg_loss = 0.854 | metric = 0.81, avg_metric = 0.98
Epoch 5/200 | Iter 500/703 | training loss = 0.530, avg_loss = 0.847 | metric = 0.83, avg_metric = 0.97
Epoch 5/200 | Iter 600/703 | training loss = 0.550, avg_loss = 0.840 | metric = 0.84, avg_metric = 0.97
Epoch 5/200 | Iter 700/703 | training loss = 0.614, avg_loss = 0.833 | metric = 0.81, avg_metric = 0.96
Training consumes 295.13 second
validate epoch 5
Epoch 5/200 | Iter 0/78 | metric = 1.64, avg_metric = 1.64
Evaluation of validation result: average L2 distance = 0.89319
Validation consumes 15.06 second
Epoch 5 is now the best epoch with metric 0.8932
我最终训练了大概155个epoch效果就不错了,作为参考,给出155个epoch时验证集的指标:
Epoch 155 is now the best epoch with metric 0.1790
其实本论文除去数据集处理和损失函数稍微麻烦一些外,其他部分要实现并不困难。
3.3 网络预测(Inference)
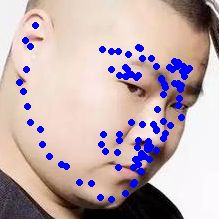
实际要使用的时候,该网络前面应该还要增加一个人脸检测网络,因为输入该网络的图像应该是人脸检测得到的bbox图像。当然,数据集提供的测试集已经裁剪好了,可以直接进行测试看效果。如果想测试自己的图像,可以自己手动裁一下人脸区域查看结果。我自己百度找的人脸图像输入网络后的效果图如下:
3.4 总结感悟
复现期间,自己的网络出了一些问题。后来参考了github上PFLD-pytorch项目里的实现细节后,进行了一些修改。包括:
- 损失函数的微调;
- 数据增广的实现等。
经过对比实验发现,深度学习果然还是数据驱动的算法,其实就算损失函数或者网络结构的实现有一些不同,得到的效果其实还是相差不大。但是如果没有数据增广,网络最终的效果就差的比较多(metric=0.179 <-> metric=0.553)。比如我用未增广的数据训练了500epoch后得到的效果:
可以看到,正脸还差强人意,但是已经明显要差很多了。一旦遇到侧脸这种更难的情况,网络的鲁棒性明显就不足。
当然,论文提供的在损失函数中融入三维信息的思想,还是很值得学习的。