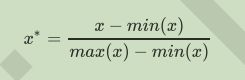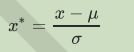天气晴 小马真的是怕冷星人 天天都是在冷冷冷中度过 哈哈哈
周六周日休息了两天 学习了线代 这两天忙于新学期选课 从今天下午开始 又要努力这周的项目任务啦
今日目标:
1. matlab实现数据预处理和特征工程
2. 对matlab中的SVM算法代码进行了解
/*
本文重点讲解:数据归一化、数据标准化、特征工程中的特征选择
其中用Matlab代码实现了归一化、标准化、PCA降维算法(使用自带的pca函数)
*/
数据挖掘五大流程:
1.获取数据
2.数据预处理
数据预处理是从数据中检测,纠正或删除损坏,不准确或不适用于模型的记录的过程
可能面对的问题有:数据类型不同,比如有的是文字,有的是数字,有的含时间序列,有的连续,有的间断。也可能,数据的质量不行,有噪声,有异常,有缺失,数据出错,量纲不一,有重复,数据是偏态,数据量太大或太小
数据预处理的目的:让数据适应模型,匹配模型的需求
3.特征工程
特征工程是将原始数据转换为更能代表预测模型的潜在问题的特征的过程,可以通过挑选最相关的特征,提取特征以及创造特征来实现。其中创造特征又经常以降维算法的方式实现。可能面对的问题有:特征之间有相关性,特征和标签无关,特征太多或太小,或者干脆就无法表现出应有的数据现象或无法展示数据的真实面貌。
特征工程的目的:1) 降低计算成本,2) 提升模型上限
4. 建模,测试模型并预测出结果
5.上线,验证模型效果
数据预处理 Preprocessing & Impute
数据无量纲化
在机器学习算法实践中,我们往往有着将不同规格的数据转换到同一规格,或不同分布的数据转换到某个特定分布的需求,这种需求统称为将数据“无量纲化”。数据的无量纲化可以是线性的,也可以是非线性的。线性的无量纲化包括中心化(Zero-centered或者Mean-subtraction)处理和缩放处理(Scale)。中心化的本质是让所有记录减去一个固定值,即让数据样本数据平移到某个位置。缩放的本质是通过除以一个固定值,将数据固定在某个范围之中,取对数也算是一种缩放处理。
(1)数据归一化(Normalization,又称Min-Max Scaling)
当数据(x)按照最小值中心化后,再按极差(最大值 - 最小值)缩放,数据移动了最小值个单位,并且会被收敛到[0,1]之间,而这个过程,就叫做数据归一化(Normalization,又称Min-Max Scaling)。注意,Normalization是归一化,不是正则化,真正的正则化是regularization,不是数据预处理的一种手段。
Matlab实现代码:
%导入数据集和导入数据两种
%(1)导入数据集
load wine_SVM; %wine表示数据集
[m,n] = size(wine);
normal = zeros(m,n);
for i = 1:m
ma = max( wine(i,:) ); %求数据集的最大值
mi = min( wine(i,:) ); %求数据集的最小值
normal(i,:) = ( wine(i,:)-mi )./( ma-mi ); %对数据集进行归一化
end
wine_normal = normal;
%(2)导入数据
A = [-1,2; -0.5,6; 0,10; 1,18] %导入数据
%数据归一化代码
A_nor = (A - min(A)) ./ (max(A)-min(A))
Matlab点除符号的使用
matlab 找矩阵中每行或每列的最大值和最小值
已知矩阵a:
1、找矩阵a每列的最大值
[max_a,index]=max(a);
或者[max_a,index]=max(a,[],1);
其中max_a是最大的数值,index是最大的数值所处的位置。【最小值由min替换max即可】
2、找矩阵a每行的最大值
[max_a,index]=max(a,[],2);
其中max_a是最大的数值,index是最大的数值所处的位置。【最小值由min替换max即可】
【注意,有时需要找除0以外的最小值,可以将矩阵中的0值置为NaN: a(find(a==0))=NaN;
将NaN重新置为0:a(find(isnan(a)==1))=0;】
(2)数据标准化(StandardScaler):把数据变成标准正态分布
当数据(x)按均值(μ)中心化后,再按标准差(σ)缩放,数据就会服从为均值为0,方差为1的正态分布(即标准正态分布),而这个过程,就叫做数据标准化(Standardization,又称Z-score normalization)。
Matlab实现代码:
%导入数据集和导入数据两种
%(1)导入数据集
load wine_SVM; %wine表示数据集
[m,n] = size(wine);
normal = zeros(m,n);
for i = 1:m
mea = mean( wine(i,:) ); %求数据集的均值
va = var( wine(i,:) ); %求数据集的方差
normal(i,:) = ( wine(i,:)-mea )/va; %对数据集进行标准化
end
wine_normal = normal;
%(2)导入数据
A = [-1,2; -0.5,6; 0,10; 1,18]; %导入数据
%数据标准化代码
A_nor = (A - mean(A)) ./ var(A)
(3)StandardScaler 和 MinMaxScaler选哪个?
看情况。大多数机器学习算法中,会选择StandardScaler来进行特征缩放,因为MinMaxScaler对异常值非常敏感。在PCA,聚类,逻辑回归,支持向量机,神经网络这些算法中,StandardScaler往往是最好的选择。
MinMaxScaler在不涉及距离度量、梯度、协方差计算以及数据需要被压缩到特定区间时使用广泛,比如数字图像处理中量化像素强度时,都会使用MinMaxScaler将数据压缩于[0,1]区间之中。
建议先试试看StandardScaler,效果不好换MinMaxScaler。
特征工程(Feature Engineering)
特征提取(feature extraction):从文字,图像,声音等其他非结构化数据中提取新信息作为特征。比如说,从淘宝宝贝的名称中提取出产品类别,产品颜色,是否是网红产品等等。
特征创造(feature creation):把现有特征进行组合,或互相计算,得到新的特征。比如说,我们有一列特征是速度,一列特征是距离,我们就可以通过让两列相处,创造新的特征:通过距离所花的时间。
特征选择(feature selection):从所有的特征中,选择出有意义,对模型有帮助的特征,以避免必须将所有特征都导入模型去训练的情况。
今天重点学习特征选择!!!
我们有四种方法可以用来选择特征:过滤法,嵌入法,包装法,和降维算法。
(1)过滤法( Filter)
1)方差过滤:这是通过特征本身的方差来筛选特征的类。比如一个特征本身的方差很小,就表示样本在这个特征上基本没有差异,可能特征中的大多数值都一样,甚至整个特征的取值都相同,那这个特征对于样本区分没有什么作用。所以无论接下来的特征工程要做什么,都要优先消除方差为0的特征。
在现实中,我们只会使用阈值为0或者阈值很小的方差过滤,来为我们优先消除一些明显用不到的特征,然后我们会选择更优的特征选择方法继续削减特征数量。
过滤法的主要对象是:需要遍历特征或升维的算法们,而过滤法的主要目的是:在维持算法表现的前提下,帮助算法们降低计算成本。
2)相关性过滤<卡方(分类问题)、F检验(分类和回归)、互信息>:我们希望选出与标签相关且有意义的特征,因为这样的特征能够为我们提供大量信息。如果特征与标签无关,那只会白白浪费我们的计算内存,可能还会给模型带来噪音。我们的目的是要删除与标签无关的特征,保留与标签相关且有意义的特征。
卡方过滤是专门针对离散型标签(即分类问题)的相关性过滤。卡方检验计算每个非负特征和标签之间的卡方统计量,并依照卡方统计量由高到低为特征排名,我们可以借此除去最可能独立于标签,与我们分类目的无关的特征。
F检验,又称ANOVA,方差齐性检验,是用来捕捉每个特征与标签之间的线性关系的过滤方法。它即可以做回归也可以做分类,其中F检验分类用于标签是离散型变量的数据,而F检验回归用于标签是连续型变量的数据。
互信息法是用来捕捉每个特征与标签之间的任意关系(包括线性和非线性关系)的过滤方法。和F检验相似,它既可以做回归也可以做分类。不过互信息法比F检验更加强大,F检验只能够找出线性关系,而互信息法可以找出任意关系。它返回“每个特征与目标之间的互信息量的估计”,这个估计量在[0,1]之间取值,为0则表示两个变量独立,为1则表示两个变量完全相关。
3)通常来说,先使用方差过滤,然后使用互信息法来捕捉相关性。
(2)嵌入法(Embedded)
优点: 嵌入法是一种让算法自己决定使用哪些特征的方法,即特征选择和算法训练同时进行。在使用嵌入法时,我们先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据权值系数从大到小选择特征。这些权值系数往往代表了特征对于模型的某种贡献或某种重要性,比如决策树和树的集成模型中的feature_importances_属性,可以列出各个特征对树的建立的贡献,我们就可以基于这种贡献的评估,找出对模型建立最有用的特征。因此相比于过滤法,嵌入法的结果会更加精确到模型的效用本身,对于提高模型效力有更好的效果。并且,由于考虑特征对模型的贡献,因此无关的特征(需要相关性过滤的特征)和无区分度的特征(需要方差过滤的特征)都会因为缺乏对模型的贡献而被删除掉,可谓是过滤法的进化版。
缺点: 过滤法中使用的统计量可以使用统计知识和常识来查找范围(如p值应当低于显著性水平0.05),而嵌入法中使用的权值系数却没有这样的范围可找——我们可以说,权值系数为0的特征对模型丝毫没有作用,但当大量特征都对模型有贡献且贡献不一时,我们就很难去界定一个有效的临界值。这种情况下,模型权值系数就是我们的超参数,我们或许需要学习曲线,或者根据模型本身的某些性质去判断这个超参数的最佳值究竟应该是多少。
(3)包装法(Wrapper)
包装法也是一个特征选择和算法训练同时进行的方法,与嵌入法十分相似,它也是依赖于算法自身的选择,比如coef_属性或feature_importances_属性来完成特征选择。但不同的是,我们往往使用一个目标函数作为黑盒来帮助我们选取特征,而不是自己输入某个评估指标或统计量的阈值。包装法在初始特征集上训练评估器,并且通过coef_属性或通过feature_importances_属性获得每个特征的重要性。然后,从当前的一组特征中修剪最不重要的特征。在修剪的集合上递归地重复该过程,直到最终到达所需数量的要选择的特征。区别于过滤法和嵌入法的一次训练解决所有问题,包装法要使用特征子集进行多次训练,因此它所需要的计算成本是最高的。
(4)降维算法
什么是维度?
对于数组和Series来说,维度就是功能shape返回的结果,shape中返回了几个数字,就是几维。索引以外的数据,不分行列的叫一维(此时shape返回唯一的维度上的数据个数),有行列之分叫二维(shape返回行x列),也称为表。一张表最多二维,复数的表构成了更高的维度。当一个数组中存在2张3行4列的表时,shape返回的是(更高维,行,列)。当数组中存在2组2张3行4列的表时,数据就是4维,shape返回(2,2,3,4)。
数组中的每一张表,都可以是一个特征矩阵或一个DataFrame,这些结构永远只有一张表,所以一定有行列,其中行是样本,列是特征。针对每一张表,维度指的是样本的数量或特征的数量,一般无特别说明,指的都是特征的数量。除了索引之外,一个特征是一维,两个特征是二维,n个特征是n维。
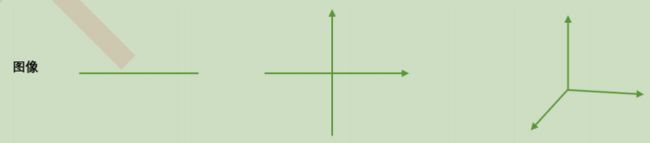
对图像来说,维度就是图像中特征向量的数量。特征向量可以理解为是坐标轴,一个特征向量定义一条直线,是一维,两个相互垂直的特征向量定义一个平面,即一个直角坐标系,就是二维,三个相互垂直的特征向量定义一个空间,即一个立体直角坐标系,就是三维。三个以上的特征向量相互垂直,定义人眼无法看见,也无法想象的高维空间。
降维算法中的”降维“,指的是降低特征矩阵中特征的数量。降维的目的是为了让算法运算更快,效果更好,但其实还有另一种需求:数据可视化。从上面的图我们其实可以看得出,图像和特征矩阵的维度是可以相互对应的,即一个特征对应一个特征向量,对应一条坐标轴。所以,三维及以下的特征矩阵,是可以被可视化的,这可以帮助我们很快地理解数据的分布,而三维以上特征矩阵的则不能被可视化,数据的性质也就比较难理解。
SVD和主成分分析PCA都属于矩阵分解算法中的入门算法,都是通过分解特征矩阵来进行降维。
主成分分析降维算法Matlab实现:
%PCA主成分分析
%导入数据集,设置主成分分析的阈值为95
threshold = 95;
[mtrain,ntrain] = size(train_wine);
[mtest,ntest] = size(test_wine);
dataset = [train_wine;test_wine];
%用Matlab自带的pca函数进行主成分分析
[dataset_coef,dataset_score,dataset_latent,tsquared,explained]= pca(dataset);
%对数据集特征贡献度进行分析并画图
dataset_cumsum = 100*cumsum(dataset_latent)./sum(dataset_latent);
index = find(dataset_cumsum >= threshold);
percent_explained = 100*dataset_latent/sum(dataset_latent);
figure;
pareto(percent_explained);
xlabel('Principal Component');
ylabel('Variance Explained (%)');
grid on;
%生成主成分分析后降维的数据集
train_pca = dataset_score(1:mtrain,:);
test_pca = dataset_score( (mtrain+1):(mtrain+mtest),: );
train_pca = train_pca(:,1:index(1));
test_pca = test_pca(:,1:index(1));
附上Matlab自带的pca函数参考资料链接 :https://blog.csdn.net/qq_25800311/article/details/83385029