各种距离概念与计算公式

参考：
范数：https://blog.csdn.net/xdy1120/article/details/106426504
各种距离：https://www.cnblogs.com/AlvinSui/p/8931074.html
常见的距离算法和相似度（相关系数）计算方法：https://www.cnblogs.com/arachis/p/Similarity.html
距离与范数：https://zhuanlan.zhihu.com/p/363707147

一、各种距离概念

距离这个概念，在上小学的时候就知道了，它衡量的是两点之间的远近程度。其实距离根据定义可以分为好多好多种，我们日常生活中的距离指的一般是欧式距离。在很多文献中都会讲到距离，比如曼哈顿距离、欧式距离和闵可夫斯基距离等。这些概念往往看一遍就懂了，但是在没有看概念的前提下让你描述一遍往往会一时语塞。所以笔者准备进行一下汇总并进行一些区分。

1、曼哈顿距离

出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

曼哈顿这个城市的街道很有特点，因为它方方正正的，就像坐标轴上的坐标格网一样。在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

2、欧式距离

欧几里得度量（euclidean metric）也称欧氏距离，是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。

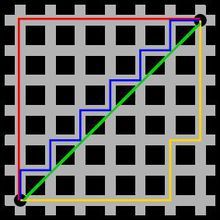
下图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。

3、切比雪夫距离

二个点之间的切比雪夫距离（Chebyshev Distance）定义是其各坐标数值差绝对值的最大值。国际象棋棋盘上两个位置间的切比雪夫距离是指王要从一个位子移至另一个位子最少需要走的步数（王可以直行、横行、斜行）。

4、闵可夫斯基距离

闵氏空间指狭义相对论中由一个时间维和三个空间维组成的时空，为俄裔德国数学家闵可夫斯基(H.Minkowski,1864-1909)最先表述。闵氏距离（Minkowski Distance）不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。闵氏距离有时也指时空间隔，其计算方式详见下文

5、标准化欧式距离

标准化欧氏距离（Standardized Euclidean Distance）是针对欧氏距离的缺点而作的一种改进。标准欧氏距离的思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等（也就是将数据投影到N(0,1)区间），再根据标准化之后的数据计算欧式距离。

6、马氏距离

马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的，表示点与一个分布之间的距离。它是一种有效的计算两个未知样本集的相似度的方法。

马氏距离又称为数据的协方差距离，它是一种有效的计算两个未知样本集的相似度的方法。马氏距离的结果也是将数据投影到N(0,1)区间并求其欧式距离，与标准化欧氏距离不同的是它认为各个维度之间不是独立分布的，所以马氏距离考虑到各种特性之间的联系。它的计算用到协方差矩阵，当协方差矩阵是对角阵（即各维度之间独立）时，马氏距离也就等于标准化欧式距离。下图表示了欧式距离和马氏距离的区别，黑线为到中心距离相等的点的集合。

7、余弦距离

几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。下图中的 $cos\theta$ 就是指余弦距离（Cosine Distance），它的取值范围为$[-1,1]$，而$dis(A,B)$就是指的欧式距离。

8、汉明距离

汉明距离（Hamming Distance）是使用在数据传输差错控制编码里面的，汉明距离表示两个（相同长度）字对应位不同的数量，我们以d（x,y）表示两个字x,y之间的汉明距离。对两个字符串进行异或运算，并统计结果为1的个数，那么这个数就是汉明距离。比如

• 1011101 与 1001001 之间的汉明距离是 2。
• 2143896 与 2233796 之间的汉明距离是 3。

9、杰卡德距离

杰卡德距离(Jaccard Distance) 是用来衡量两个集合差异性的一种指标，它是杰卡德相似系数的补集，被定义为1减去Jaccard相似系数。而杰卡德相似系数(Jaccard similarity coefficient)，也称杰卡德指数(Jaccard Index)，是用来衡量两个集合相似度的一种指标。

• Jaccard相似指数用来度量两个集合之间的相似性，它被定义为两个集合交集的元素个数除以并集的元素个数。
• Jaccard距离用来度量两个集合之间的差异性，它是Jaccard的相似系数的补集，被定义为1减去Jaccard相似系数。

10、相关距离

相关距离(Correlation distance)是用来衡量向量X与Y差异程度的一种方法，它被定义为1减去相关系数。相关系数是衡量向量X与Y相关程度的一种方法，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。

11、信息熵

以上的距离度量方法度量的皆为两个样本（向量）之间的距离，而信息熵描述的是整个系统内部样本之间的一个距离，或者称之为系统内样本分布的集中程度（一致程度）、分散程度、混乱程度（不一致程度）。系统内样本分布越分散(或者说分布越平均)，信息熵就越大。分布越有序（或者说分布越集中），信息熵就越小。

二、各种距离计算公式

三、范数与距离

向量的范数可以简单形象的理解为向量的长度，或者向量到零点的距离，或者相应的两个点之间的距离。

常用的向量的范数：

• L0范数：L0范数并不是一个真正的范数，它主要被用来度量向量中非零元素的个数。
• L1范数: ||x|| 为x向量各个元素绝对值之和。
• L2范数: ||x||为x向量各个元素平方和的1/2次方，L2范数又称Euclidean范数或者Frobenius范数。
• Lp范数: ||x||为x向量各个元素绝对值p次方和的1/p次方。
• L∞范数: ||x||为x向量各个元素绝对值最大那个元素的绝对值

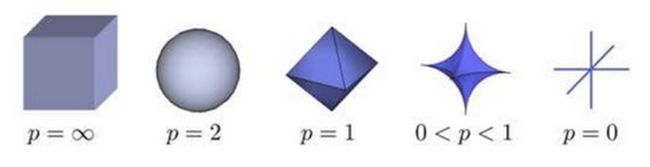
可以看到闵可夫斯基距离就是p-norm范数的一般化定义。下图给出了一个Lp球（||X||p=1）的形状随着P的减少的可视化图：