数据结构—排序
一、Comparable接口介绍
Java提供了一个接口comparable用来定义排序规则,实现对对象的排序。
需求:
- 定义一个学生类Student,具有年龄age和姓名name两个属性,并通过Comparable接口提供比较规则。
- 定义测试类,在测试类中定义测试方法Comparable getMax(Comparable c1,Comparable c2)完成测试。
class Student implements Comparable<Student>{
private int age;
private String name;
//省略set,get,toString,构造器
//重写compareTo方法,用于比较学生年龄大小
@Override
public int compareTo(Student o) {
int result=this.age-o.age;
return result;
}
public static void main(String[] args) {
Student s1=new Student(18,"张三");
Student s2=new Student(20, "李四");
int result=s1.compareTo(s2);
if (result>0) {
System.out.println(s1.toString());
}else {
System.out.println(s2.toString());
}
}
编写工具类Utils,用于比较数据大小和做数据替换
public class Utils {
//比较数值大小
public static boolean greater(Comparable v,Comparable w) {
return v.compareTo(w)>0;
}
//数值替换
public static void exch(Comparable[] a,int i,int j) {
Comparable temp;
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}
二、冒泡排序
1. 排序原理
-
比较相邻的元素,如果前一个元素比后一个元素大,就交换这两个元素的位置。
-
对每一对相邻元素做同样的工作,从一开始第一位元素到结尾最后一位元素,最终最后位置的元素就是最大值。
(从最后一位元素到第一位元素,最终第一位元素就是最小值)。
2. 代码实现
冒泡排序的时间复杂度为O(N^2)。
代码实现1:
public class BubbleSort2 {
public static void main(String[] args) {
int[] s= {4,8,2,6,7,5,1};
bubbleSort(s);
for (int i = 0; i < s.length; i++) {
System.out.println(s[i]);
}
}
private static void bubbleSort(int[] s) {
int temp;
for (int i = 0; i < s.length; i++) {
for (int j = s.length-1; j >i; j--) {
if (s[j]<s[j-1]) {
temp=s[j];
s[j]=s[j-1];
s[j-1]=temp;
}
}
}
}
}
public class BubbleSort {
public static void bubbleSort(Comparable[] s) {
for (int i = 0; i < s.length; i++) {
for (int j = s.length-1; j >i; j--) {
if (Utils.greater(s[j], s[j-1])) {
Utils.exch(s, j, j-1);
}
}
}
}
public static void main(String[] args) {
Integer[] s= {9,7,4,8,2,5,3,1,6};
bubbleSort(s);
// 输出排序后的序列
System.out.print(Arrays.toString(s));
}
}
3. 算法优化
public class OptimizeBubbleSorting {
private static void bubbleSort(Comparable[] s) {
for (int i = 0; i < s.length-1; i++) {
boolean flag=true; //使用flag来标明在一轮比较中是否发生数据交换
for (int j = s.length-1; j>i; j--) {
if (Utils.greater(s[j], s[j-1])) {
Utils.exch(s, j, j-1);
flag=false; //若发生数据交换则置为false
}
}
if (flag) { //判断flag的值,若还为true说明在一轮比较中没有发生数据交换,直接退出
return;
}
}
}
public static void main(String[] args) {
Integer[] s= {9,7,4,8,2,5,3,1,6};
bubbleSort(s);
// 输出排序后的序列
System.out.print(Arrays.toString(s));
}
}
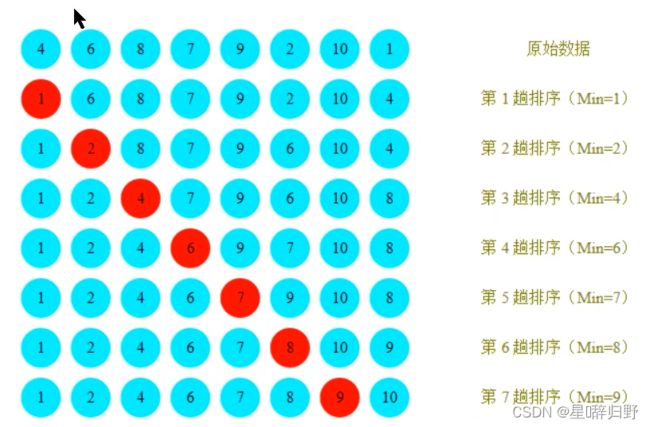
三、选择排序
1. 排序原理
- 每一次遍历的过程,都假定第一个索引处的元素是最小值,和其他索引处的值依次进行比较,如果当前索引处的值大于某个索引处的值,则假定其他某个索引处的值为最小值,最后可以找到最小值所在的索引。
- 交换第一个索引处和最小值所在索引处的值。
2. 代码实现
时间复杂度:O(n^2)
代码实现1:
public class SelectionSort {
public static void main(String[] args) {
int[] s= {9,8,6,3,7,2,4,1,5};
selectionSort(s);
for (int i = 0; i < s.length; i++) {
System.out.println(s[i]);
}
}
private static void selectionSort(int[] s) {
for (int i = 0; i < s.length-1; i++) {
int min=i;//定义一个变量,记录最小元素所在的索引,默认为参与选择排序的第一个元素所在的位置
for (int j = i+1; j < s.length; j++) {
//需要比较最小索引min处的值和j索引处的值
if (s[min]>s[j]) {
min=j;
}
}
//交换最小元素所在索引min处的值和索引i处的值
int temp=s[min];
s[min]=s[i];
s[i]=temp;
}
}
}
代码实现2:
public class SelectionSort2 {
public static void main(String[] args) {
Integer[] s= {9,7,4,8,2,5,3,1,6};
selectionSort(s);
// 输出排序后的序列
System.out.print(Arrays.toString(s));
}
private static void selectionSort(Comparable[] s) {
for (int i = 0; i < s.length-1; i++) {
//定义一个变量,记录最小元素所在的索引,默认为参与选择排序的第一个元素所在的位置
int min=i;
for (int j = i+1; j < s.length; j++) {
//需要比较最小索引min处的值和j索引处的值
if (Utils.greater(s[min], s[j])) {
min=j;
}
}
//交换最小元素所在索引min处的值和索引i处的值
Utils.exch(s, min, i);
}
}
}
四、插入排序
1. 排序原理
- 把所有的元素分为两组,已排序的和未排序的。
- 找到未排序的组中的第一个元素,向已经插入的组中进行插入。
- 倒叙遍历已经排序的元素,依次和待插入的元素进行比较,直到找到一个元素小于带插入的元素,那么就把待插入的元素放到这个位置,其他元素向后移动一位。
2. 代码实现
时间复杂度:O(n^2)
代码实现1:
public class InsertionSort {
public static void main(String[] args) {
int[] s= {4,3,2,10,12,1,5,6};
insertionSort(s);
for (int i = 0; i < s.length; i++) {
System.out.println(s[i]);
}
}
private static void insertionSort(int[] s) {
int temp;//用于替换的中间变量
//已排序的数组
for (int i = 0; i < s.length-1; i++) {
//找出未排序的第一个元素
for (int j = i+1; j>0; j--) {
//未排序的第一个元素与一排序的数组进行比较
if (s[j]<s[j-1]) {
temp=s[j];
s[j]=s[j-1];
s[j-1]=temp;
}
}
}
}
}
代码实现2:
public class InsertionSort2 {
public static void main(String[] args) {
Integer[] s= {1,7,4,6,3,5,2,8,9};
insertionSort2(s);
System.out.println(Arrays.toString(s));
}
private static void insertionSort2(Comparable[] s) {
for (int i = 0; i < s.length-1; i++) {
for (int j = i+1; j > 0; j--) {
if (Utils.greater(s[j],s[j-1])) {
Utils.exch(s,j,j-1);
}
}
}
}
}
五、希尔排序
1. 排序原理
2. 代码实现
代码实现1:
public class ShellSort {
public static void main(String[] args) {
Integer[] s= {1,7,4,6,3,5,2,8,9};
shellSort(s);
System.out.println(Arrays.toString(s));
}
private static void shellSort(Comparable[] s) {
//根据数组a的长度,确定增长量h的初始值
int h=1;
while (h<s.length/2) {
h=2*h+1;
}
//希尔排序
while (h>=1) {
//排序
//找到待插入的元素
for (int i = h; i < s.length; i++) {
//把待插入的元素插入到有序序列中
for (int j = i; j >= h; j-=h) {
//待插入的元素是a[j],比较a[j],a[j-h]
if (Utils.greater(s[j-h], s[j])) {
Utils.exch(s, j, j-h);
}else {
break;
}
}
}
//减小h的值
h=h/2;
System.out.println(Arrays.toString(s));
}
}
}
代码实现2:
public class ShellSort2 {
public static void main(String[] args) {
int[] s= {6,3,8,7,9,5,1,2};
shellSort(s);
for (int i = 0; i < s.length; i++) {
System.out.println(s[i]);
}
}
private static void shellSort(int[] s) {
int temp;
int h=1;
while (h<s.length/2) {
h=2*h+1;
}
while (h>=1) {
for (int i = h; i < s.length; i++) {
for (int j = i; j >=h; j=j-h) {
if (s[j]<s[j-h]) {
temp=s[j];
s[j]=s[j-h];
s[j-h]=temp;
}
}
}
h=h/2;
}
}
}
六、递归
1. 定义
定义方法时,在方法内部调用方法本身,称为递归。
在递归时,不能无限制的调用自己,必须要有边界条件,能够让递归结束,因为每一次递归调用都会在栈内存开辟新的空间重新执行方法,如果递归的层级太深,很容易造成栈溢出。
2. 需求
定义一个方法,使用递归完成求n的阶乘。
public static long factional(int n) {
//求n的阶乘
if (n==1) {
return 1;
}
return n*factional(n-1);
}
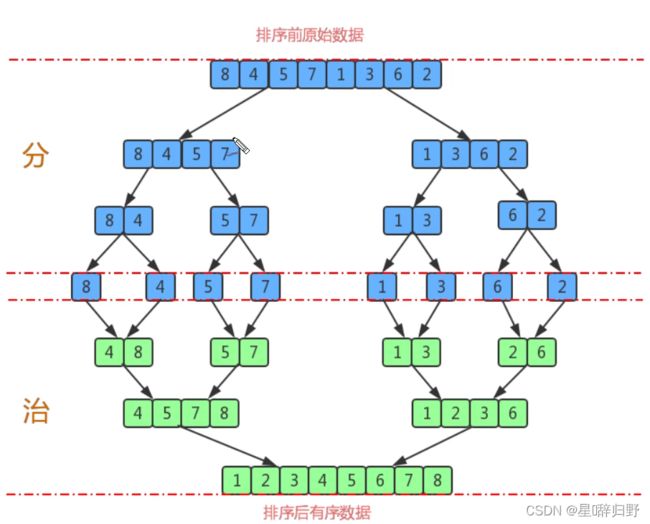
七、归并排序
1. 排序原理
- 尽可能的一组数据拆分成两个元素相等的子组,并对每一个子组继续拆分,直到拆分后的每个子组的元素个数为1为止。
- 将相邻的两个子组进行合并成一个有序的大组
- 不断地重复步骤2,直到最终只有一个组为止
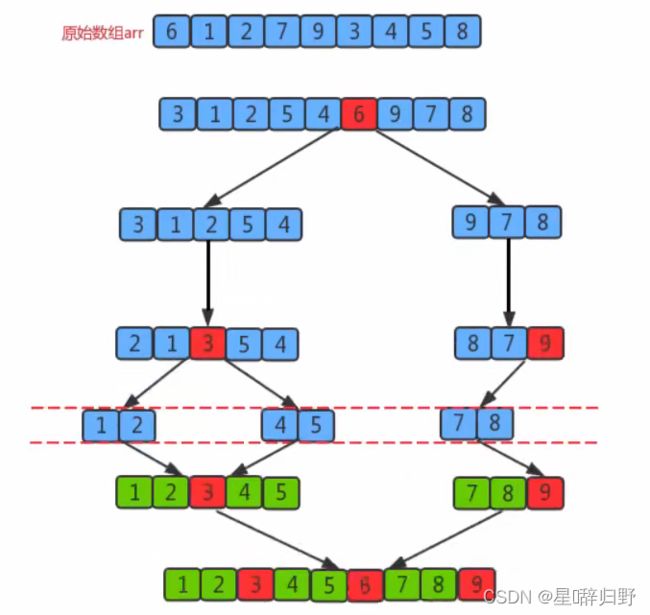
八、快速排序
1. 排序原理
-
首先设定一个分界值,通过该分界值将数组分成左右两部分
-
将大于或等于分界值的数据放到数组右边,小于分界值的数据放到数组左边,此时左边部分各元素都小于或等于分界值,而右边各部分中元素都大于或等于分界值。
-
然后左边和右边的数据可以独立排序,对于左侧的数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值,右侧的数组数据也可做类似处理。
-
重复上述过程,可以看出,这是一个递归定义,通过递归将左侧部分排好序后,再递归拍好右侧部分的顺序,当左侧和右侧两个部分的数据拍完序后,整个数组的排序也就完成了。