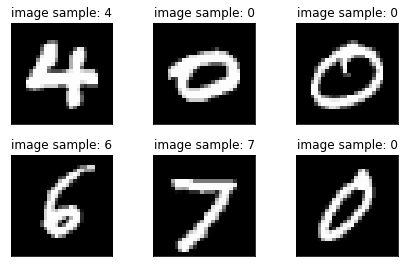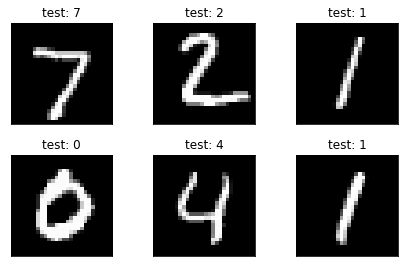一文让你完全弄懂逻辑回归和分类问题实战《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础（上）（DL笔记整理系列）

好吧，只好拆分为上下两篇发布了>_<

终于肝出来了，今天就是除夕夜了，祝大家新快乐！^q^

---

《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础 （上）（逻辑回归、Softmax回归、信息论基础）（DL笔记整理系列）

[email protected]

https://fanfansann.blog.csdn.net/

https://github.com/fanfansann/fanfan-deep-learning-note

作者：繁凡

version 1.0  2022-1-20

 

声明：

1）《繁凡的深度学习笔记》是我自学完成深度学习相关的教材、课程、论文、项目实战等内容之后，自我总结整理创作的学习笔记。写文章就图一乐，大家能看得开心，能学到些许知识，对我而言就已经足够了 ^q^ 。

2）因个人时间、能力和水平有限，本文并非由我个人完全原创，文章部分内容整理自互联网上的各种资源，引用内容标注在每章末的参考资料之中。

3）本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益，还望海涵，并联系博主删除，非常感谢各位为知识传播做出的贡献！

4）本人才疏学浅，整理总结的时候难免出错，还望各位前辈不吝指正，谢谢。

5）本文由我个人（ CSDN 博主 「繁凡さん」（博客） ， 知乎答主 「繁凡」（专栏）， Github 「fanfansann」（全部源码） ， 微信公众号 「繁凡的小岛来信」（文章 P D F 下载））整理创作而成，且仅发布于这四个平台，仅做交流学习使用，无任何商业用途。

6）「我希望能够创作出一本清晰易懂、可爱有趣、内容详实的深度学习笔记，而不仅仅只是知识的简单堆砌。」

7）本文《繁凡的深度学习笔记》全汇总链接：《繁凡的深度学习笔记》前言、目录大纲

8）本文的Github 地址：https://github.com/fanfansann/fanfan-deep-learning-note/ 孩子的第一个 『Github』！给我个 $\boxed{⭐\text{Starred}}$ 嘛！谢谢！！o(〃＾▽＾〃)o

9）此属 version 1.0 ，若有错误，还需继续修正与增删，还望大家多多指点。本文会随着我的深入学习不断地进行完善更新，Github 中的 P D F 版也会尽量每月进行一次更新，所以建议点赞收藏分享加关注，以便经常过来回看！

如果觉得还不错或者能对你有一点点帮助的话，请帮我给本篇文章点个赞，你的支持是我创作的最大动力！^0^

要是没人点赞的话自然就更新慢咯 >_<

一文让你完全弄懂 信息论基础 与 softmax 回归实战《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础（下）目录：
    3.3 信息论基础
      3.3.1 信息论
      3.3.2 香农熵
      3.3.3 相对熵（KL 散度）
      3.3.4 交叉熵
      3.3.5 JS 散度
      3.3.6 Wasserstein 距离
      3.3.7 结构化概率模型
    3.4 Softmax 回归
      3.4.1 Softmax 回归模型
      3.4.2 优化方法
      3.4.3 权重衰减
      3.4.4 Fashion-MNIST 数据集图片分类实战
    3.5 Softmax 回归与逻辑回归的关系
      3.5.1 Softmax 回归与逻辑回归的关系
      3.5.2 多分类问题的 Softmax 回归与 k 个二元分类器
    3.6 面试问题集锦
    3.7 参考资料

本章话题 第 3 章（上）（点击即可跳转哟）：
话题 1 ：什么是分类问题？

《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础 （上）

话题 1 ：什么是分类问题？

分类问题（classification），即找一个函数判断输入数据所属的类别，也即预测预测值属于某一段连续的实数区间的方法。分类问题可以是二类别问题（是 / 不是），也可以是多类别问题（在多种类别中判断输入数据具体属于哪一个类别）。与回归问题（regression）相比，分类问题的输出不再是连续值，而是离散值，用来指定其属于哪个类别。分类问题在现实中应用非常广泛，比如垃圾邮件识别，手写数字识别，人脸识别，语音识别等。

图源：[15]

  

  本章我们先从简单的多分类手写数字图片分类问题实战开始入手，使用 简单神经网络 解决分类问题，带大家切身体会一下分类问题的流程以及神经网络的魅力，我们将在第 6 章 神经网络与反向传播算法 中详细讲解神经网络，并使用诸如 通用逼近定理（universal approximation theorem）等理论来尝试说明神经网络为何如此强大。在体验完神经网络解决手写数字分类问题以后，我们将详细介绍机器学习中关于分类问题的线性分类器：解决二分类问题的 逻辑回归 以及由其拓展而来的解决多分类问题的 softmax 回归，理解和掌握这些理论，是机器学习的基础。

3.1 手写数字分类问题

3.1.1 手写数字图片数据集

  我们前面讲过机器学习是一种需要从数据中间学习的行为，因在解决机器学习问题之前我们需要先采集大量的真实样本数据 $(x,y)$ 。我们以手写的数字图片识别为例，如图 3.1 所示，我们需要收集大量的由真人书写的 $0\sim 9$​​ 的数字图片，为了便于存储和计算，一般把收集的原始图片缩放到某个固定的大小 (Size 或 Shape)，比如图片有 $224$​​ 个像素的行和 $224$​​ 个像素的列，则称图片大小为 $224\times 224$​​。我们将这张图片作为一组输入数据的 $x$​​。

图 3.1 手写数字图片示例

  

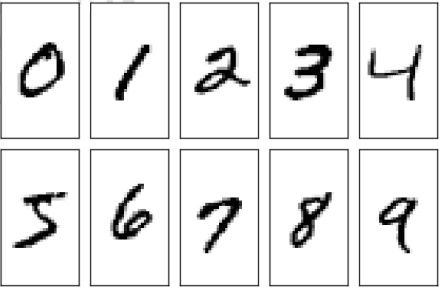
  同时，我们需要给每一张图片标注一个标签，也即图片的真实分类 $y$​​​​​ ，表明这张图片属于哪一个具体的类别，我们一般通过映射方式将类别名一一对应到从 $0$​​​​​ 开始编号的数字，比如说硬币的正反面，我们可以用 $0$​​​​​ 来表示硬币的反面，用 $1$​​​​​ 来表示硬币的正面，当然也可以反过来。这种编码方式叫作数字编码（Number Encoding）。手写数字图片识别问题编码则更为直观，我们直接使用数字的 $0\sim 9$​​​​​ 来表示类别名字为 $0\sim 9$​​​​​​ 的图片。

  如果希望模型能够在新样本上也能具有良好的表现，即模型泛化能力 （GeneralizationAbility）较好，那么我们应该尽可能多地增加数据集的规模和多样性（Variance），使得我们用于学习的训练数据集与真实的手写数字图片的分布（Ground-truth Distribution）尽可能的逼近，这样在训练数据集上面学到了模型能够很好的用于未见过的手写数字图片的预测。所以我们一般根据 $82$ 原则也即将数据集按照 $8:2$ 的比例拆分为训练集（Training Set）和测试集（Test Set）。

  机器学习的主要目的就是从训练集上学习到数据的真实模型，从而能够在未见过的测试集上也能够表现良好。为了确保我们量化一下模型在训练集和测试集上的表现，将其分别称为 训练误差 (training error) 和 测试误差 (test error) ，后者也经常称为 泛化误差 (generalization error) 。可以说，理想的模型就是在最小化训练误差的同时，最小化泛化误差。因此为了评估和测试各种算法的性能，不同问题下的统一且质量高的数据集必不可少。在手写数字图片识别问题下，Lecun, Bottou, Bengio, & Haffner 于 1998 年发布了名为 $\text{MNIST}$​​ 的手写数字图片数据集，它包含了 $0\sim 9$​​​ 共 $10$​​​ 种数字的手写图片，每种数字一共有 $7000$​​​ 张图片，采集自不同书写风格的真实手写图片，一共 $70000$​​​ 张图片。其中 $60000$​​​ 张图片作为训练集 ${\mathbb{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$​​​ ，用来训练模型，剩下 $10000$​​​ 张图片作为测试集 ${\mathbb{D}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$​​​ ，用来测试模型的效果。训练集和测试集共同组成了整个 $\text{MNIST}$ 数据集 。

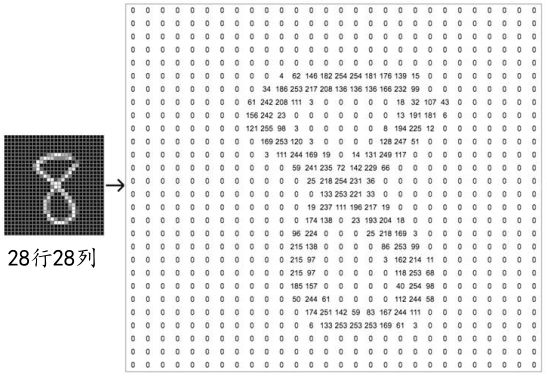
  考虑到手写数字图片包含的信息比较简单，每张数字图片均被缩放到了统一的 $28\times 28$ 的大小，同时只保留了灰度信息，如图 3.2 所示。这些图片由真人书写，包含了如字体大小、书写风格、粗细等丰富的样式，确保这些图片的分布与真实的手写数字图片的分布尽可能的接近，从而保证了模型的泛化能力。

图 3.2 MNIST手写数字图片示例

  

  每张图片包含了 $h$​​​​​ 行（Height/Row）， $w$​​​​​ 列（Width/Column），每个位置保存了像素（Pixel）值，像素值一般使用 $0\sim 255$​​​​​ 的整形数值来表达颜色的强度信息，例如可以让 $0$​​​​​ 表示强度最低，$255$​​​​​ 表示强度最高。如果是彩色图片，则每个像素点包含了 R、G、B 三个通道的强度信息，分别代表三原色红、绿、蓝的红色通道、绿色通道、蓝色通道的颜色强度，所以与灰度图片不同，它的每个像素点使用一个 $1$​​​​​ 维、长度为 $3$​​​​​ 的向量（Vector） 来表示，向量的 $3$​​​​​ 个元素依次代表了当前像素点上面的 R、G、B 颜色强度，因此彩色图片需要保存为形状是 $[h,w,3]$​​​​​ 的张量（Tensor，可以理解为 $3$​​ 维数组）。如果是灰度图片，则直接使用一个数值来表示灰度强度即可。如图 3.3 所示，令 $0$​​​​​ 表示纯黑，$255$​​​​​ 表示纯白，因此它只需要一个形为 $[h,w]$​​​​​ 的二维矩阵（Matrix）来表示一张图片信息（当然也可以保存为 $[h,w,1]$​​​​​​ 形状的张量）。

图 3.3 图的表示示意图

  

3.1.2 构建模型

  回顾我们在回归问题讨论的生物神经元结构。我们把一组长度为 $d_{in}$​ 的输入向量 $\mathbf{x}=[x_1,x_2,\dots ,x_{d_{in}}{]}^{\mathrm{T}}$​ 简化为单输入标量 $x$​，模型可以表达成 $y=x\times w+b$​ 。如果是多输入、单输出的模型结构的话，我们需要借助于向量形式：

$$y={\mathbf{w}}^T\mathbf{x}+b=\left[w_1,w_2,w_3,\dots ,w_{d_{\mathrm{i}\mathrm{n}}}\right]\cdot \left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ \cdots \\ x_{d_{\mathrm{i}\mathrm{n}}}\end{array}\right]+b\text{\hspace{1em}(3.1)}$$

更一般地，通过组合多个多输入、单输出的神经元模型，可以拼成一个多输入、多输出的模型：
$$y=\mathbf{w}\cdot \mathbf{x}+b\text{\hspace{1em}(3.2)}$$

其中，$\mathbf{x}\in R^{d_{\mathrm{i}\mathrm{n}}},\mathbf{b}\in R^{d_{\mathrm{o}\mathrm{u}\mathrm{t}}},\mathbf{y}\in R^{d_{\mathrm{o}\mathrm{u}\mathrm{t}}},W\in R^{d_{\mathrm{o}\mathrm{u}\mathrm{t}}\times d_{\mathrm{i}\mathrm{n}}}$。

对于多输出节点、批量训练方式，我们将模型写成张量形式：
$$Y=X@W+b\text{\hspace{1em}(3.3)}$$

  其中 $X\in R^{b\times d_{\mathrm{i}\mathrm{n}}},\mathbf{b}\in R^{d_{\mathrm{o}\mathrm{u}\mathrm{t}}},Y\in R^{b\times d_{\mathrm{o}\mathrm{u}\mathrm{t}}},W\in R^{d_{\mathrm{i}\mathrm{n}}\times d_{\mathrm{o}\mathrm{u}\mathrm{t}}}$​。$d_{\mathrm{i}\mathrm{n}}$​ 表示输入节点数，$d_{\mathrm{o}\mathrm{u}\mathrm{t}}$​ 表示输出节点数。张量 $X$​ shape 为 $[b,d_{\mathrm{i}\mathrm{n}}]$​ ，表示 $b$​ 个样本的输入数据，每个样本的特征长度为 $d_{\mathrm{i}\mathrm{n}}$​ ；张量 $W$​ 的 shape 为 $[d_{\mathrm{i}\mathrm{n}},d_{\mathrm{o}\mathrm{u}\mathrm{t}}]$​，共包含了 $d_{\mathrm{i}\mathrm{n}}\times d_{\mathrm{o}\mathrm{u}\mathrm{t}}$​ 个网络参数；偏置向量 $\mathbf{b}$​ 的 shape 为 $d_{\mathrm{o}\mathrm{u}\mathrm{t}}$​ ，每个输出节点上均添加一个偏置值；@符号表示矩阵相乘（Matrix Multiplication，matmul）。

考虑两个样本，输入特征长度 $d_{\mathrm{i}\mathrm{n}}=3$​ ，输出特征长度 $d_{\mathrm{o}\mathrm{u}\mathrm{t}}=2$​ 的模型，公式展开为
$$\left[\begin{array}{ll}{o}_1^1& o_2^1\\ o_1^2& o_2^2\end{array}\right]=\left[\begin{array}{lll}{x}_1^1& x_2^1& x_3^1\\ x_1^2& x_2^2& x_3^2\end{array}\right]\left[\begin{array}{ll}{w}_{11}& w_{12}\\ w_{21}& w_{22}\\ w_{31}& w_{32}\end{array}\right]+\left[\begin{array}{l}{b}_1\\ b_2\end{array}\right]\text{\hspace{1em}(3.4)}$$

其中 $x_1^1$​ 等符号的上标表示样本索引号，下标表示样本向量的元素。对应模型结构图如图 3.4 所示：

图 3.4 3 输入 2 输出模型

  

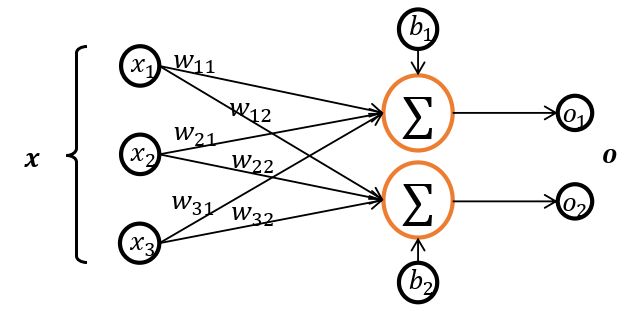
  可以看到，通过张量形式表达网络结构，更加简洁清晰，同时也可充分利用张量计算的并行加速能力。那么怎么将图片识别任务的输入和输出转变为满足格式要求的张量形式呢?

  考虑输入格式，一张图片 $\mathbf{x}$ 使用矩阵方式存储，shape 为：$[h,w]$ ，$b$ 张图片使用 shape 为 $[b,h,w]$ 的张量 $X$ 存储。而我们模型只能接受向量形式的输入特征向量，因此需要将 $[h,w]$ 的矩阵形式图片特征按顺序平铺成 $[h\times w]$ 长度的向量 $[b,h\times w]$，如图 3.5 所示，其中输入特征的长度 $d_{\mathrm{i}\mathrm{n}}=h\times w$。

图 3.5 打平

  

  对于输出标签，前面我们已经介绍了数字编码，它可以用一个数字来表示便签信息。但是数字编码一个最大的问题是，数字之间存在天然的大小关系，比如 $1<2<3$，如果 1、2、3 分别对应的标签是猫、狗、鱼，他们之间并没有大小关系，所以采用数字编码的时候会迫使模型去学习到这种不必要的约束。

  那么怎么解决这个问题呢？可以将输出设置为 $d_{\mathrm{o}\mathrm{u}\mathrm{t}}$​ 个输出节点的向量，$d_{\mathrm{o}\mathrm{u}\mathrm{t}}$​ 与类别数相同，让第 $i(i\in d_{\mathrm{o}\mathrm{u}\mathrm{t}})$​个输出值表示当前样本属于类别 $i$​ 的概率 $P_i$​。我们只考虑输入图片只输入一个类别的情况，此时输入图片的真实的标注已经明确：如果物体属于第 $i$​ 类的话，那么索引为 $i$​ 的位置上设置为 $1$​，其他位置设置为 $0$​，我们把这种编码方式叫做 one-hot 编码。

  手写数字图片的总类别数有 10 种，即输出节点数$d_{\mathrm{o}\mathrm{u}\mathrm{t}}=10$ ，那么对于某个样本，假设它属于类别 $i$ ，即图片的中数字为 $i$ ，只需要一个长度为 $10$ 的向量 $\mathbf{y}$，向量 $\mathbf{y}$ 的索引号为 $i$ 的元素设置为 $1$，其他位为 $0$。

  比如图片 $0$​ 的 One-hot 编码为 [1,0,0,… ,0]，图片 $2$​ 的 Onehot 编码为[0,0,1,… ,0]，图片 $9$​ 的One-hot 编码为 [0,0,0, … ,1]。One-hot 编码是非常稀疏(Sparse)的，相对于数字编码来说，占用较多的存储空间，所以一般在存储时还是采用数字编码，在计算时，根据需要来把数字编码转换成 One-hot 编码，通过 tf.one_hot 即可实现。

$\text{ In }[2]:$

y = tf.constant([0, 1, 2, 3, 9])
y = tf.one_hot(y, depth = 10)
y

$\text{ Out }[2]:$

tf.Tensor(
[[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]], shape=(5, 10), dtype=float32)

PyTorch 中的 one_hot 实现如下：
$\text{ In }[3]:$​

def one_hot(label, depth = 10): 
 # one-hot 编码函数，depth 设置向量长度 
    out = torch.zeros(label.size(0), depth) 
    idx = torch.LongTensor(label).view(-1, 1) 
    out.scatter_(dim = 1, index = idx, value = 1) 
    return out 
 
y = torch.tensor([0, 1, 2, 3]) # 数字编码的 4 个样本标签 
y = one_hot(y, depth = 10) # one-hot 编码，指定类别总数为 10 
print(y) 

$\text{ Out }[3]:$

tensor( 
[[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] # 数字 0 的 one-hot 编码向量 
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] # 数字 1 的 one-hot 编码向量 
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.] # 数字 2 的 one-hot 编码向量 
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]])

  对于手写数字图片识别任务而言，输入是一张打平后的图片向量 $\mathbf{x}\in R^{28\ast 28}$ ，输出是一个长度为 $10$ 的向量 $R^{10}$ ，图片的真实标签 $\mathbf{y}$ 经过 one-hot 编码后变成长度为 $10$​ 的稀疏向量。

  预测模型采用多输入、多输出的线性模型 $o={\mathbf{W}}^{\mathrm{T}}\mathbf{x}+b$，其中模型的输出记为输入的预测值 $o$ ，我们希望 $o$ 越接近真实标签 $\mathbf{y}$ 越好。我们一般把输入经过一次 (线性) 变换叫做一层网络。

3.1.3 误差计算

  对于分类问题来说，我们的目标是最大化某个性能指标，比如准确度 $\mathrm{a}\mathrm{c}\mathrm{c}=\frac{\text{分类正确的个数}}{\text{测试集的总数}}$​，但是当我们把准确度当做损失函数去优化时，会发现 $\frac{\partial \mathrm{a}\mathrm{c}\mathrm{c}}{\partial \theta }$​ 是不可导的，因此无法利用梯度下降算法优化网络参数 $\theta$​。

  一般的解决方法是：设立一个平滑可导的代理目标函数，比如优化模型的输出与 Onehot 编码后的真实标签 $\mathbf{y}$ 之间的距离(Distance)，通过优化代理目标函数得到的模型，一般在测试性能上也能有良好的表现。

  因此，相对回归问题而言，分类问题的优化目标函数和评价目标函数是不一致的。模型的训练目标是通过优化损失函数 $\mathcal{L}$ 来找到最优数值解 ：
$${\mathrm{W}}^{\ast },{\mathbf{b}}^{\ast }=\underset{W,\mathbf{b}}{\mathrm{argmin}}\mathcal{L}(\mathbf{o},\mathbf{y})\text{\hspace{1em}(3.5)}$$

  对于分类问题的误差计算来说，更常见的是采用交叉熵(Cross entropy)损失函数，而不是采用回归问题中介绍的均方差损失函数。我们将在 3.3信息论基础 中介绍交叉熵损失函数，这里先继续采用 MSE 损失函数来求解手写数字识别问题。对于 $N$​​ 个样本的均方差损失函数可以表达为：
$$\mathcal{L}(\mathbf{o},\mathbf{y})=\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^{10}{\left(o_j^i-y_j^i\right)}^2\text{\hspace{1em}(3.6)}$$

  现在我们只需要采用梯度下降算法来优化损失函数得到 $\mathbf{W},\mathbf{b}$ 的最优解，利用求得的模型去预测未知的手写数字图片 $\mathbf{x}\in {\mathbb{D}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$​​ ，即可得到预测的准确度。

3.1.4 非线性模型

我们目前为止使用的仍然是线性模型，显然是不能够胜任分类问题这一任务的。我们在 2.3.1 非线性模型 中讲解了线性模型转换为非线性模型进行拟合以及表达能力的相关概念，考虑转换为非线性模型并且增加模型的表达能力。

$❑$ 非线性模型

显然我们只需要使用激活函数即可转换为非线性模型。我们将在第 6 章 神经网络与反向传播算法 6.4 激活函数 中对激活函数进行详细的讲解，这里选择 ReLU 函数作为激活函数，使得线性模型的输出 $\mathbf{W}\mathbf{x}+\mathbf{b}$ 通过激活函数，即可得到非线性模型输出 $\mathbf{o}$ ：
$$\mathbf{o}=\mathrm{ReLU}(\mathbf{W}\mathbf{x}+\mathbf{b})\text{\hspace{1em}(3.7)}$$

$❑$ 表达能力

  针对于模型的表达能力偏弱的问题，我们通过重复堆叠多次变换来增加其表达能力：

$${\mathbf{h}}_1=\mathrm{ReLU}\left({\mathbf{W}}_1\mathbf{x}+{\mathbf{b}}_1\right)\text{\hspace{1em}(3.8)}$$

$${\mathbf{h}}_2=\mathrm{ReLU}\left({\mathbf{W}}_2{\mathbf{h}}_1+{\mathbf{b}}_2\right)\text{\hspace{1em}(3.9)}$$

$$\mathbf{o}={\mathbf{W}}_3{\mathbf{h}}_2+{\mathbf{b}}_3\text{\hspace{1em}(3.10)}$$

  把第一层神经元的输出值 ${\mathbf{h}}_1$ 作为第二层神经元模型的输入，把第二层神经元的输出 ${\mathbf{h}}_2$ 作为第三层神经元的输入，最后一层神经元的输出作为模型的输出即可。

  从网络结构上看，如图 3.6 所示，函数的嵌套表现为网络层的前后相连，每堆叠一个(非)线性环节，网络层数增加一层。

图 3.6 神经网络

  

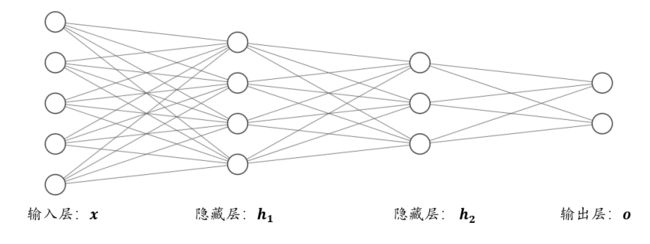
  我们把数据节点所在的层叫做输入层，每一个非线性模块的输出 ${\mathbf{h}}_{\mathbf{i}}$​ 连同它的网络层参数 ${\mathbf{W}}_{\mathbf{i}}$​ 和 ${\mathbf{b}}_{\mathbf{i}}$​ 称为一层网络层，特别地，对于网络中间的层，叫做隐藏层，最后一层叫做输出层。这种由大量神经元模型连接形成的网络结构称为（前馈）神经网络(Neural Network)。

  现在我们的网络模型已经升级为为 $3$ 层的神经网络，具有较好的非线性表达能力，接下来我们讨论怎么优化网络。

$❑$ 优化方法

  对于仅一层的网络模型，如线性回归的模型，我们可以直接推导出 $\frac{\partial L}{\partial w}$ 和 $\frac{\partial L}{\partial b}$ 的表达式，然后直接计算每一步的梯度，根据梯度更新法则循环更新 $w,b$ 参数即可。

  但是，当网络层数增加、数据特征长度增大、添加复杂的非线性函数之后，模型的表达式将变得非常复杂，很难手动推导出梯度的计算公式；而且一旦网络结构发生变动，网络的函数模型也随之发生改变，依赖人工去计算梯度的方式显然不可行。

  这个时候就是深度学习框架发明的意义所在，所有深度学习框架都至少要支持一种技术，也就是自动求导（Autograd）技术。借助于自动求导，深度学习框架在计算函数的损失函数的过程中，会记录模型的计算图模型，并自动完成任意参数 $\theta$​ 的偏导分 $\frac{\partial L}{\partial \theta }$​ 的计算，用户只需要搭建出网络结构，梯度将自动完成计算和更新，使用起来非常便捷高效。

3.1.4 手写数字图片识别实战

我们这里分别使用 TensorFlow2.0 与 PyTorch 对手写数字图片识别进行实战。

3.1.4.1 TensorFlow2.0 实现

$❑$​ Step 0 引入文件并设置图像参数

$\text{ In }[1]:$

%matplotlib inline
# “在 jupyter notebook 在线使用 matplotlib”，为 IPython 的内置 magic 函数，在 Pycharm 中不被支持
import os
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow.keras.datasets as datasets

plt.rcParams['font.size'] = 16
plt.rcParams['font.family'] = ['STKaiti']
plt.rcParams['axes.unicode_minus'] = False

$❑$ Step 1 导入数据并对数据进行处理

  利用 TensorFlow 自动在线下载 MNIST 数据集，并转换为 Numpy 数组格式。

$\text{ In }[2]:$

def load_data() :
    # 加载 MNIST 数据集 元组tuple: (x, y), (x_val, y_val)
    (x, y), (x_val, y_val) = datasets.mnist.load_data()
    # 将 x 转换为浮点张量，并从 0 ~ 255 缩放到 [0, 1.] - 1 -> [-1, 1] 即缩放到 -1 ~ 1
    x = tf.convert_to_tensor(x, dtype = tf.float32) / 255. - 1
    # 转换为整形张量
    y = tf.convert_to_tensor(y, dtype = tf.int32)
    # one-hot 编码
    y = tf.one_hot(y, depth = 10)
    # 改变视图， [b, 28, 28] => [b, 28*28]
    x = tf.reshape(x, (-1, 28 * 28))
    # 构建数据集对象
    train_dataset = tf.data.Dataset.from_tensor_slices((x, y))
    # 批量训练
    train_dataset = train_dataset.batch(200)
    return train_dataset

   TensorFlow 中的 load_data() 函数返回两个元组 (tuple) 对象，第一个是训练集，第二个是测试集，每个 tuple 的第一个元素是多个训练图片数据 $X$ ，第二个元素是训练图片对应的类别数字 $Y$。其中训练集 $X$ 的大小为 $(60000,28,28)$ ，代表了 $60000$ 个样本，每个样本由 $28$ 行、$28$ 列构成，由于是灰度图片，故没有 RGB 通道；训练集 $Y$ 的大小为 $(60000)$，代表了这 $60000$ 个样本的标签数字，每个样本标签用一个 $0\sim 9$ 的数字表示，测试集同理。

  从 TensorFlow 中加载的 MNIST 数据图片，数值的范围在 $[0,255]$ 之间。在机器学习中间，一般希望数据的范围在 $0$ 周围小范围内分布。我们可以通过预处理步骤，我们把 $[0,255]$ 像素范围归一化(Normalize)到 $[0,1.]$ 区间，再缩放到 $[-1,1]$ 区间，从而有利于模型的训练。

  每一张图片的计算流程是通用的，我们在计算的过程中可以一次进行多张图片的计算，充分利用 CPU 或 GPU 的并行计算能力。一张图片我们用 shape 为 $[h,w]$ 的矩阵来表示，对于多张图片来说，我们在前面添加一个数量维度 （Dimension），使用 shape 为 $[b,h,w]$ 的张量来表示，其中的 $b$ 代表了 batch size(批量。多张彩色图片可以使用 shape 为 $[b,h,w,c]$ 的张量来表示，其中的 $c$ 表示通道数量（Channel），彩色图片$c=3$（R、G、B）。通过 TensorFlow 的Dataset 对象可以方便完成模型的批量训练，只需要调用 batch() 函数即可构建带 batch 功能的数据集对象。

$❑$ Step 2 网络搭建

  对于第一层模型来说，他接受的输入 $\mathbf{x}\in {\mathbb{R}}^{784}$ ，输出 ∈ ${\mathbb{R}}^{256}$ 设计为长度为 $256$ 的向量，我们不需要显式地编写 ${\mathbf{h}}_1=\mathrm{ReLU}\left({\mathbf{W}}_1\mathbf{x}+{\mathbf{b}}_1\right)$ 的计算逻辑，在 TensorFlow 中通过一行代码即可实现：

layers.Dense(256, activation = 'relu') 

  使用 TensorFlow 的 Sequential 容器可以非常方便地搭建多层的网络。对于 3 层网络，我们可以通过

keras.sequential([
    layers.Dense(256, activation = 'relu'),
    layers.Dense(128, activation = 'relu'),
    layers.Dense(10)])

  快速完成 $3$ 层网络的搭建，第 $1$ 层的输出节点数设计为 $256$，第 $2$ 层设计为 $128$，输出层节点数设计为 $10$。直接调用这个模型对象 model(x) 就可以返回模型最后一层的输出 。

  为了能让大家理解更多的细节，我们这里不使用上面的框架，手动实现经过 3 层神经网络。

对神经网络参数初始化：

$\text{ In }[3]:$

def init_paramaters() :
    # 每层的张量需要被优化，使用 Variable 类型，并使用截断的正太分布初始化权值张量
    # 偏置向量初始化为 0 即可
    # 第一层参数
    w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev = 0.1))
    b1 = tf.Variable(tf.zeros([256]))
    # 第二层参数
    w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev = 0.1))
    b2 = tf.Variable(tf.zeros([128]))
    # 第三层参数
    w3 = tf.Variable(tf.random.truncated_normal([128, 10], stddev = 0.1))
    b3 = tf.Variable(tf.zeros([10]))
    return w1, b1, w2, b2, w3, b3

$❑$ Step 3 模型训练

  得到模型输出 $\mathbf{o}$ 后，通过 MSE 损失函数计算当前的误差 $\mathcal{L}$：

with tf.GradientTape() as tape:#构建梯度记录环境
    #打平，[b,28,28] =>[b,784]
    x=tf.reshape(x,(-1,28*28))
    #step1. 得到模型输出 output
    # [b,784] =>[b,10]
    out=model(x)

手动实现代码：

    with tf.GradientTape() as tape :#构建梯度记录环境
            # 第一层计算， [b, 784]@[784, 256] + [256] => [b, 256] + [256] => [b,256] + [b, 256]
            h1 = x @ w1 + tf.broadcast_to(b1, (x.shape[0], 256))
            # 通过激活函数 relu
            h1 = tf.nn.relu(h1)
            # 第二层计算， [b, 256] => [b, 128]
            h2 = h1 @ w2 + b2
            h2 = tf.nn.relu(h2)
            # 输出层计算， [b, 128] => [b, 10]
            out = h2 @ w3 + b3

$❑$ Step 4 梯度优化

  利用 TensorFlow 提供的自动求导函数 tape.gradient(loss, model.trainable_variables) 求出模型中所有的梯度信息 $\frac{\partial L}{\partial \theta }$ , $\theta \in \{{\mathbf{W}}_1,{\mathbf{b}}_1,{\mathbf{W}}_2,{\mathbf{b}}_2,{\mathbf{W}}_3,{\mathbf{b}}_3\}$：

 grads = tape.gradient(loss, model.trainable_variables) 

  计算获得的梯度结果使用 grads 变量保存。再使用 optimizers 对象自动按着梯度更新法则
$${\theta }^{\prime }=\theta -\eta \times \frac{\partial \mathcal{L}}{\partial \theta }\text{\hspace{1em}(3.11)}$$

去更新模型的参数 $\theta$。

grads = tape.gradient(loss, model.trainable_variables)
 # w' = w - lr * grad，更新网络参数
optimizer.apply_gradients(zip(grads, model.trainable_variables)) 

  循环迭代多次后，就可以利用学好的模型 $f_{\theta }$ 去预测未知的图片的类别概率分布。

手动实现梯度更新代码如下：

$\text{ In }[4]:$​

def train_epoch(epoch, train_dataset, w1, b1, w2, b2, w3, b3, lr = 0.001) :
    for step, (x, y) in enumerate(train_dataset) :
        with tf.GradientTape() as tape :
            # 第一层计算， [b, 784]@[784, 256] + [256] => [b, 256] + [256] => [b,256] + [b, 256]
            h1 = x @ w1 + tf.broadcast_to(b1, (x.shape[0], 256))
            # 通过激活函数 relu
            h1 = tf.nn.relu(h1)
            # 第二层计算， [b, 256] => [b, 128]
            h2 = h1 @ w2 + b2
            h2 = tf.nn.relu(h2)
            # 输出层计算， [b, 128] => [b, 10]
            out = h2 @ w3 + b3

            # 计算网络输出与标签之间的均方差， mse = mean(sum(y - out) ^ 2)
            # [b, 10]
            loss = tf.square(y - out)
            # 误差标量， mean: scalar
            loss = tf.reduce_mean(loss) 
            # 自动梯度，需要求梯度的张量有[w1, b1, w2, b2, w3, b3]
            grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])

        # 梯度更新， assign_sub 将当前值减去参数值，原地更新
        w1.assign_sub(lr * grads[0])
        b1.assign_sub(lr * grads[1])
        w2.assign_sub(lr * grads[2])
        b2.assign_sub(lr * grads[3])
        w3.assign_sub(lr * grads[4])
        b3.assign_sub(lr * grads[5])

        if step % 100 == 0 :
            print(epoch, step, 'loss:', loss.numpy())

    return loss.numpy()

整体的代码思路如下：

   我们首先创建每个非线性层的 $\mathbf{W}$ 和 $\mathbf{b}$ 张量参数，然后把 $\mathbf{x}$ 的 shape=[b, 28, 28] 转成向量 [b, 784] ，然后计算三层神经网络，每层使用 ReLU 激活函数，然后与 one_hot 编码的 $\mathbf{y}$ 一起计算均方差，利用 tape.gradient() 函数自动求梯度

$${\theta }^{\prime }=\theta -\eta \cdot \frac{\partial \mathcal{L}}{\partial \theta }\text{\hspace{1em}(3.12)}$$

  使用 assign_sub() 函数按照上述梯度下降算法更新网络参数（assign_sub()将自身减去给定的参数值，实现参数的原地 (In-place) 更新操作），最后使用 matplotlib 绘制图像输出即可。

$\text{ In }[5]:$

def train(epochs) :
    losses = []
    train_dataset = load_data()
    w1, b1, w2, b2, w3, b3 = init_paramaters()
    for epoch in range(epochs) :
        loss = train_epoch(epoch, train_dataset, w1, b1, w2, b2, w3, b3, lr = 0.01)
        losses.append(loss)
    x = [i for i in range(0, epochs)]
    # 绘制曲线
    plt.plot(x, losses, color = 'cornflowerblue', marker = 's', label = '训练', markersize='3')
    plt.xlabel('Epoch')
    plt.ylabel('MSE')
    plt.legend()
    plt.savefig('MNIST数据集的前向传播训练误差曲线.png')
    plt.show()
    plt.close()

if __name__ == '__main__' :
	# x 轴 0 ~ 50
    train(epochs = 50)

$\text{ Out }[5]:$

epoch:0, iteration:0, loss:2.8238346576690674
epoch:0, iteration:100, loss:0.12282778322696686
epoch:0, iteration:200, loss:0.09311732649803162
epoch:1, iteration:0, loss:0.08501865714788437
epoch:1, iteration:100, loss:0.08542951196432114
epoch:1, iteration:200, loss:0.0726892277598381
epoch:2, iteration:0, loss:0.0702851265668869
epoch:2, iteration:100, loss:0.07322590798139572
epoch:2, iteration:200, loss:0.06422527879476547
epoch:3, iteration:0, loss:0.06337807327508926
epoch:3, iteration:100, loss:0.06658075749874115
epoch:3, iteration:200, loss:0.05931859463453293
......

MNIST数据集的前向传播训练误差曲线

  

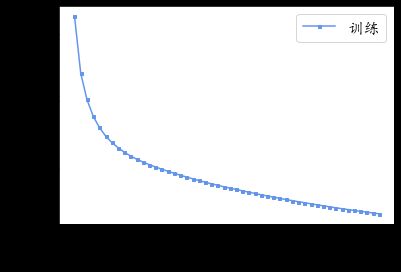
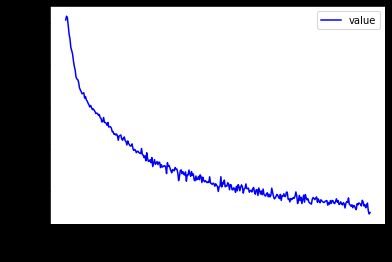
  手写数字图片 MNIST 数据集的训练误差曲线如上图所示，由于 $3$​ 层的神经网络表达能力较强，手写数字图片识别任务简单，误差值可以较快速、稳定地下降，其中对数据集的所有图片迭代一遍叫做一个 Epoch，我们可以在间隔数个 Epoch 后测试模型的准确率等指标，方便监控模型的训练效果。

3.1.4.2 PyTorch 实现

完整代码详见：Github（ Python 文件及 Jupyter Notebook 文件）

$\text{ In }[1]:$​

%matplotlib inline
import os
import sys
import time
import torch # 导入 pytorch 
import sklearn
import torchvision # 导入视觉库
import numpy as np
import pandas as pd
from torch import nn # 导入网络层子库
from torch import optim # 导入优化器
from torchsummary import summary # 从 torchsummary 工具包中导入 summary 函数
from torch.nn import functional as F # 导入网络层函数子库
from matplotlib import pyplot as plt
from utils import one_hot, plot_curve, plot_image

print(sys.version_info)
for module in torch, torchvision, np, pd, sklearn:
    print(module.__name__, module.__version__)

$\text{ Out }[1]:$​

sys.version_info(major=3, minor=8, micro=5, releaselevel='final', serial=0)
torch 1.10.2
torchvision 0.11.3
numpy 1.19.3
pandas 1.3.3
sklearn 0.22.2.post1

$\text{ In }[2]:$​​

''''   超参数   '''
batch_size = 512 # 批大小
n_epochs = 3
# 学习率
learning_rate = 0.01
# 动量
momentum = 0.9
'''  Hyperparameters   '''

$\text{ In }[3]:$​​

'''  Step 1 下载训练集和测试集，对数据进行预处理  '''
# 训练数据集，从网络下载 MNIST数据集 保存至 mnist_data 文件夹中
# 创建 DataLoader 对象 (iterable, 类似 list，可用 iter() 进行访问)，方便批量训练，将数据标准化在 0 附近并随机打散
train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train = True, download = True,
                                     # 图片预处理
                                     transform = torchvision.transforms.Compose([
                                         # 转换为张量
                                         torchvision.transforms.ToTensor(),
                                         # 标准化
                                         torchvision.transforms.Normalize(
                                         (0.1307,), (0.3081,))
                                     ])),
    batch_size = batch_size, shuffle = True)

test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data/', train = False, download = True,
                                     transform = torchvision.transforms.Compose([
                                         torchvision.transforms.ToTensor(),
                                         torchvision.transforms.Normalize(
                                         (0.1307,), (0.3081,)) # 使用训练集的均值和方差
                                     ])),
    batch_size = batch_size, shuffle = False)

$\text{ In }[4]:$

'''   Step 2。 展示样本数据   '''


def show_sample_image():
    # 使用 iter() 从 DataLoader 中取出 迭代器， next() 选取下一个迭代器
    x, y = next(iter(train_loader))
    # 输出数据的 shape，以及输入图片的最小最大强度值
    print(x.shape, y.shape, x.min(), x.max())
    # 使用自己封装的 polt_image() 函数对图片进行展示
    plot_image(x, y, 'image sample')
    
show_sample_image()    

$\text{ Out }[4]:$​

torch.Size([512, 1, 28, 28]) torch.Size([512]) tensor(-0.4242) tensor(2.8215)

$\text{ In }[5]:$

'''   Step 3。 搭建网络模型   '''
class Net(nn.Module):
    # 网络初始化
    def __init__(self):
        super(Net, self).__init__()
        # y = wx + b
        # 三层全连接层神经网络
        self.fc1 = nn.Linear(28 * 28, 256)
        self.fc2 = nn.Linear(256, 64)
        self.fc3 = nn.Linear(64, 10)

    # 定义神经网络前向传播逻辑
    def forward(self, x):
        # x : [b, 1, 28, 28]
        # h1 = relu(w1x + b1)
        x = F.relu(self.fc1(x))
        # h2 = relu(w2x + b2)
        x = F.relu(self.fc2(x))
        # h3 = w3h2 + b3
        x = self.fc3(x)
        # 直接返回向量 [b, 10], 通过 argmax 即可得到分类预测值
        return x 
        '''
        也可直接将向量经过 softmax 函数得到分类预测值
        return F.log_softmax(x, dim = 1)
        '''
# 使用 summary 函数之前，需要使用 device 来指定网络在 GPU 还是 CPU 运行
device = torch.device("cuda" if torch.cuda.is_available() else "gpu") 
print(torch.cuda.is_available())
net = Net().to(device)
# 所有的张量都需要进行 `.to(device)` 
print(net)
summary(net, (1, 28 * 28))
# summary(your_model, input_size=(channels, H, W))
# input_size 要求符合模型的输入要求, 用来进行前向传播

$\text{ Out }[5]:$​

True
Net(
  (fc1): Linear(in_features=784, out_features=256, bias=True)
  (fc2): Linear(in_features=256, out_features=64, bias=True)
  (fc3): Linear(in_features=64, out_features=10, bias=True)
)
----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Linear-1               [-1, 1, 256]         200,960
            Linear-2                [-1, 1, 64]          16,448
            Linear-3                [-1, 1, 10]             650
================================================================
Total params: 218,058
Trainable params: 218,058
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.83
Estimated Total Size (MB): 0.84
----------------------------------------------------------------

$\text{ In }[6]:$

'''   Step 4. 在训练集上进行训练   '''
def MNIST_trains(net):
    # 选择 SGD 随机梯度下降算法作为优化方法，导入网络参数、学习率以及动量
    optimizer = optim.SGD(net.parameters(), lr = learning_rate, momentum = momentum)
    train_loss = []
    for epoch in range(n_epochs):
        for batch_idx, (x, y) in enumerate(train_loader):
            # 将数据 x 打平
            # x: [b, 1, 28, 28] -> [b, 784]
            x = x.view(x.size(0), 28 * 28).to(device)
            # 经过神经网络 [b, 784] -> [b, 10]
            out = net(x).to(device)
            # 将数据的真实标签 y 转换为 one hot 向量
            y_one_hot = one_hot(y).to(device)
            # 计算 网络预测值 out 与 真实标签 y 的 mse 均方差
            # loss = mse(out, y_one_hot)
            loss = F.mse_loss(out, y_one_hot)
            # zero grad 清空历史梯度数据
            optimizer.zero_grad()
            # 进行反向传播，计算当前梯度
            loss.backward()
            # 根据当前梯度更新网络参数
            # w' = w - lr * grad
            optimizer.step()
            # 保存当前的损失函数值
            train_loss.append(loss.item())
            # 每 10 步 输出一次数据查看训练情况
            if batch_idx % 10 == 0:
                print(f"epoch:{epoch}, iteration:{batch_idx}, loss:{loss.item()}")
    # 绘制损失函数图像
    # [w1, b1, w2, b2, w3, b3]
    plot_curve(train_loss)
    
MNIST_trains(net)

$\text{ Out }[6]:$​

epoch:0, iteration:0, loss:0.12122594565153122
epoch:0, iteration:10, loss:0.09926386922597885
epoch:0, iteration:20, loss:0.08644484728574753
epoch:0, iteration:30, loss:0.07972756773233414
epoch:0, iteration:40, loss:0.07488133013248444
epoch:0, iteration:50, loss:0.07044463604688644
epoch:0, iteration:60, loss:0.06637724488973618
epoch:0, iteration:70, loss:0.06356173753738403
epoch:0, iteration:80, loss:0.05986356735229492
epoch:0, iteration:90, loss:0.05715459585189819
epoch:0, iteration:100, loss:0.05593841150403023
epoch:0, iteration:110, loss:0.05120903253555298
epoch:1, iteration:0, loss:0.05355915054678917
......

$\text{ In }[7]:$​

'''   Step 5. 在测试集中进行测试   '''
def MNIST_tests(net):
    # 在测试集中预测正确的总数
    total_correct = 0
    # 迭代所有测试数据
    for x, y in test_loader:
        # 将图片 x 打平
        x = x.view(x.size(0), 28 * 28).to(device)
        # 经过已经训练好的神经网络 net
        out = net(x).to(device)
        # 预测值 pred: argmax 返回指定维度最大值的索引
        # out [b, 10] -> pred [b]
        pred = out.argmax(dim = 1).to(device)
        # 计算预测值等于真实标签的样本数量
        correct = pred.eq(y.to(device)).sum().float().item()
        # 计算预测正确样本的总数
        total_correct += correct
    # 总样本数即为测试集的长度
    total_num = len(test_loader.dataset)
    # 计算正确率
    acc = total_correct / total_num
    # 输出测试正确率 acc
    print("test_acc:", acc)
    
MNIST_tests(net)

$\text{ Out }[7]:$​

test_acc: 0.8927

$\text{ In }[8]:$

'''   Step 6。 展示样本数据   '''
def show_test_sample_image(net):
    x, y = next(iter(test_loader))
    out = net(x.view(x.size(0), 28 * 28).to(device)).to(device)
    pred = out.argmax(dim = 1).to(device)
    plot_image(x, pred, 'test')
show_test_sample_image(net)

$\text{ Out }[8]:$​

---

  在体验完神经网络解决手写数字分类问题以后，我们将详细介绍机器学习中关于分类问题的线性分类器：解决二分类问题的 逻辑回归 以及由其拓展而来的解决多分类问题的 softmax 回归，理解和掌握这些理论，是机器学习的基础。

3.2 逻辑回归（Logistic Regression, LR）

  逻辑回归（Logistic Regression），是一种用于解决二分类（$0\mathrm{o}\mathrm{r}1$）问题的机器学习方法，用于估计某种事物的可能性。比如某用户购买某商品的可能性，某病人患有某种疾病的可能性，以及某广告被用户点击的可能性等。因其简单、可并行化、可解释强深受工业界喜爱。

  注意，这里用的是 “可能性” ，而非数学上的 “概率” ，逻辑回归的结果并非数学定义中的概率值，不可以直接当做概率值来用。该结果往往用于和其他特征值加权求和，而非直接相乘。

  逻辑回归与线性回归都是一种广义线性模型（generalized linear model）。逻辑回归假设因变量 $y$​ 服从伯努利分布，而线性回归假设因变量 $y$​ 服从高斯分布。 因此与线性回归有很多相同之处，去除 Sigmoid 映射函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过逻辑函数引入了非线性因素，把线性回归的结果从 $(-\infty ,\infty )$​ 映射到 $(0,1)$​，因此可以轻松拟合非线性模型处理二分类问题。

逻辑回归的本质可以理解为：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

因此在讲解逻辑回归函数之前，我们先来回顾一下什么是线性回归函数，并介绍什么是逻辑函数。

$❑$​ 线性回归函数

线性回归函数的数学表达式为：
$$y={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n={\theta }^{T}x\text{\hspace{1em}(3.13)}$$
其中 $x_i$​​​​​​ 是自变量，$y$​​​​​ 是因变量，$y$​​​​ 的值域为 $(-\infty ,\infty )$​​​，${\theta }_0$​​ 是常数项， ${\theta }_i(i=1,2,...,n)$​ 是待求系数。不同的权重 ${\theta }_i$ 反映了自变量对因变量不同的贡献程度。

$❑$ 逻辑分布函数

逻辑分布是一种连续性的概率分布，其分布函数 $F(x)$ 和密度函数 $f(x)$ 分别为：
$$\begin{array}{c}F(x)=P(X\le x)=\frac{1}{1+e^{\frac{-(x-\mu )}{\gamma }}}\\ f(x)=F^{\prime }(X\le x)=\frac{e^{-(x-\mu )/\gamma }}{\gamma {\left(1+e^{\frac{-(x-\mu )}{\gamma }}\right)}^2}\end{array}\text{\hspace{1em}(3.14)}$$

其中，$\mu$ 表示位置参数， $\gamma >0$​ 为形状参数。

密度函数 $f(x)$ 和 分布函数 $F(x)$ 的图像如图 3.7 所示：

图 3.7 逻辑回归的密度函数和分布函数

  

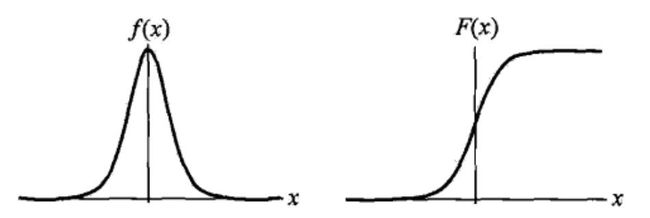
逻辑分布是由其位置和尺度参数定义的连续分布。逻辑分布的形状与正态分布的形状相似，但是逻辑分布的尾部更长，所以我们可以使用逻辑分布来建模比正态分布具有更长尾部和更高波峰的数据分布。我们最常用的 Sigmoid 函数就是逻辑的分布函数在 $\mu =0,\gamma =1$​ 时的特殊形式：

Sigmoid 函数： $g(z)=\frac{1}{1+e^{-z}}$

3.2.1 决策边界

  我们先来简述逻辑回归 $0/1$ 二分类的原理：我们通过训练的方式求出一个线性回归 $y={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n={\theta }^{T}x$​​​ 中的 $n+1$​​​ 维向量 $\theta$​​​，对于每一个新样本 $x_b$​​​，与参数 ${\theta }_i$​​​ 进行点乘，将结果带入 sigmoid 函数，得到的值为该样本发生我们定义的 $\hat{y}=1$​​​ 事件发生的概率值。如果概率大于 $0.5$​​，分类为 $1$​，否则分类为 $0$​ 。

对于公式：
$$\hat{p}=\sigma (t)=\frac{1}{1+e^{(-t)}}t={\theta }^T\cdot x_b\text{\hspace{1em}(3.15)}$$
当 $t>0$​ 时，$1<1+e^{(-t)}<2$​ ， 因此 $\hat{p}>0.5$​。当 $t>0$​ 时， $2<1+e^{(-t)}$​ 因此 $\hat{p}<0.5$。

也就是，其中有一个边界点 ${\theta }^T\cdot x_b=0$​，大于这个边界点，分类为 $1$，小于这个边界点，分类为 $0$​。我们称之为决策边界(decision boundary)。

  决策边界，也称为决策面，是用于在 $N$ 维空间，将不同类别样本分开的平面或曲面。

  决策边界 ${\theta }^T\cdot x_b=0$ 同时也代表一个直线： 假设 $\mathbf{X}$ 有两个特征 $x_1,x_2$ ，那么有线性回归函数 ${\theta }^T\cdot x_b={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2=0$​​​。这显然是一个直线，可将数据集分成两类，属于线性决策边界。

  作为能够把样本正确分类的一条边界，决策边界主要有线性决策边界（linear decision boundaries）和非线性决策边界（non-linear decision boundaries）。其中需要注意的是，决策边界是假设函数的属性，由参数决定，而不是由数据集的特征决定。

$❑$​​ 线性决策边界

线性的决策边界，如图 3.8 所示，这里的决策边界即为 $x_1+x_2-3=0$。

图 3.8 线性决策边界

  

$❑$ 非线性决策边界

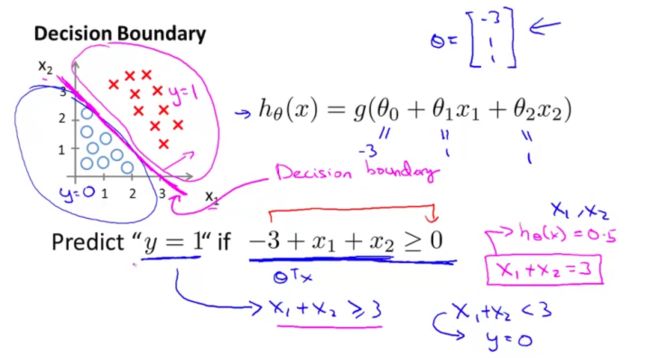
图 3.9 非线性决策边界

  

3.2.2 逻辑回归模型

  逻辑回归除了上面讲到的线性回归的决策边界以外，还需要增加一层能够找到分类概率 $P(Y=1)$ 与输入向量 $x$ 的直接关系的函数以此来判断类别。

   考虑二分类问题，给定数据集
$$D=\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right),x_i\subseteq R^n,y_i\in 0,1,i=1,2,\cdots ,N\text{\hspace{1em}(3.16)}$$

  由于我们的线性回归模型的方程为 $y={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}$​ 是一个连续的值，无法拟合离散变量，因此可以考虑用它来拟合同样取值连续的条件概率函数 $P(Y=1\mid x)$​​​。

对于参数向量 $\mathbf{w}\ne 0$ 的情况（显然若向量 $\mathbf{w}$ 为 $0$，则该模型没有任何实际意义）， 考虑 ${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}$ 的值为 $\mathbf{R}$，显然不符合概率取值为 $0\sim 1$ ，因此考虑采用广义线性模型。

最理想的是单位阶跃函数：
$$p(y=1\mid x)=\{\begin{array}{ll}0,& z<0\\ 0.5,& z=0\\ 1,& z>0\end{array},z={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}\text{\hspace{1em}(3.17)}$$
但是这个阶跃函数不可微，对数几率函数是一个常用的替代函数：
$$y=\frac{1}{1+e^{-\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}\right)}}\text{\hspace{1em}(3.18)}$$

则有：
$$\ln \frac{y}{1-y}={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}\text{\hspace{1em}(3.19)}$$
我们将 $y$ 视为 $x$ 为正例的概率，则 $1-y$ 为 $x$ 为其反例的概率。两者的比值称为几率（odds），指该事件发生与不发生的概率比值，若事件发生的概率为 $P$​。则对数几率：
$$\ln (\text{ odds })=\ln \frac{y}{1-y}\text{\hspace{1em}(3.20)}$$
将 $y$​ 视为类后验概率估计，重写公式有：
$$\begin{array}{l}{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}=\ln \frac{P(Y=1\mid x)}{1-P(Y=1\mid x)}\\ P(Y=1\mid x)=\frac{1}{1+e^{-\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}\right)}}\end{array}\text{\hspace{1em}(3.21)}$$

也就是说，输出 $Y=1$ 的对数几率是由输入 $x$ 的线性函数表示的模型，这就是逻辑回归模型。当 $y={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}$ 的值越接近正无穷，$P(Y=1\mid x)$ 概率值也就越接近 $1$​。因此逻辑回归的思路是，先拟合决策边界 (不局限于线性，还可以是多项式) ，再建立这个边界与分类的概率联系，从而得到了二分类情况下的概率。

我们最终得到的概率 $P(Y=1\mid x)=\frac{1}{1+e^{-\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}\right)}}$，我们将这里的函数 $\frac{1}{1+e^{-\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}\right)}}$ 称作 Sigmoid 函数（激活函数） $g(z)=\frac{1}{1+e^{-z}}$​：

图 3.10 Sigmoid 函数

  

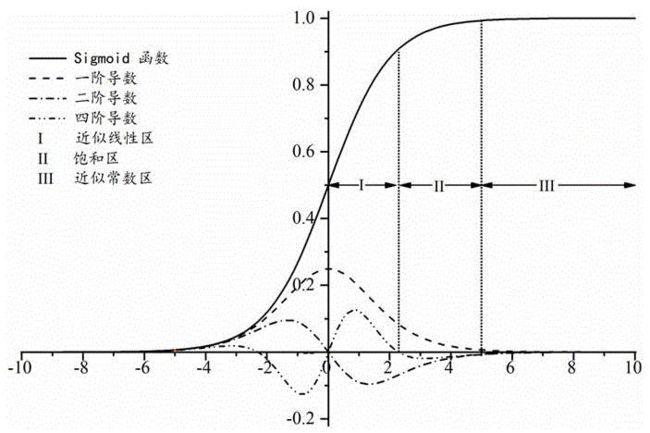
那么我们这里选择的决策函数即为：

$$P(Y=1\mid x)=g({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b})=\frac{1}{1+e^{{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+\mathbf{b}}}\text{\hspace{1em}(3.22)}$$

在逻辑回归中，激活函数 $\sigma (z)$​​​ 用于计算样本属于某类别的可能性，决策函数 $y^{\ast }=1;\mathrm{i}\mathrm{f}P(Y=1\mid x)>0.5$​​​ 用于计算给定样本的类别。

我们再来考虑一下这里使用对数几率的意义在哪里。通过上述推导我们可以看到逻辑回归实际上是使用线性回归模型的预测值逼近分类任务真实标记的对数几率，其优点有：

1. 直接对分类的概率建模，无需实现假设数据分布，从而避免了假设分布不准确带来的问题（区别于生成式模型）；
2. 不仅可预测出类别，还能得到该预测的概率，这对一些利用概率辅助决策的任务很有用；
3. 对数几率函数是任意阶可导的凸函数，有许多数值优化算法都可以求出最优解。

逻辑回归模型只能解决二分类问题，逻辑回归模型解决多分类问题有两种方法：

• 方案1：当存在样本可能属于多个标签的情况时，可以训练出 $k$ 个二分类的逻辑回归分类器。第 $i$ 个分类器用以区分每个样本是否可以归类为第 $i$ 类，训练该分类器的时候，需要把标签重新整理为第i类标签和非第 $i$ 类标签两类。通过这样的方法，就解决了每个样本可能拥有多个标签的情况。

• 方案2：若每个样本只对应于一个标签，我们可以假设每个样本属于不同标签的概率服从几何分布，使用多项式逻辑回归（Softmax Regression）来进行分类。 详见 3.3 Softmax 回归

3.2.3 代价函数

逻辑回归模型的数学形式确定后，剩下就是如何去求解模型中的参数。在统计学中，常常使用极大似然估计法来求解，即找到一组参数，使得在这组参数下，我们的数据的似然度（概率）最大。

由于逻辑回归解决二分类问题，也即仅有 $0\text{or}1$，因此设：
$$\begin{array}{l}P(y=1\mid x)=P(x)\\ P(y=0\mid x)=1-P(x)\end{array}\text{\hspace{1em}(3.23)}$$

似然函数：
$$L(w)=\prod {\left[p\left(x_i\right)\right]}^{y_i}{\left[1-p\left(x_i\right)\right]}^{1-y_i}\text{\hspace{1em}(3.24)}$$

为了更方便求解，我们对等式两边同取对数，写成对数似然函数：
$$\begin{array}{rl}L(w)& =\sum \left[y_i\ln p\left(x_i\right)+\left(1-y_i\right)\ln \left(1-p\left(x_i\right)\right)\right]\\ & =\sum \left[y_i\ln \frac{p\left(x_i\right)}{1-p\left(x_i\right)}+\ln \left(1-p\left(x_i\right)\right)\right]\\ & =\sum \left[y_i\left(w\cdot x_i\right)-\ln \left(1+e^{w\cdot x_i}\right)\right]\end{array}\text{\hspace{1em}(3.25)}$$

在机器学习中我们有损失函数的概念，其衡量的是模型预测错误的程度。如果取整个数据集上的平均对数似然损失，我们可以得到：
$$J(w)=-\frac{1}{N}\ln L(w)\text{\hspace{1em}(3.26)}$$
即在逻辑回归模型中，我们最大化似然函数和最小化损失函数实际上是等价的。

3.2.4 优化方法

优化的主要目标是找到一个方向，参数朝这个方向移动之后使得损失函数的值能够减小，这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的损失函数是：

$$J(w)=-\frac{1}{n}\left(\sum _{i=1}^n\left(y_i\ln p\left(x_i\right)+\left(1-y_i\right)\ln \left(1-p\left(x_i\right)\right)\right)\right)\text{\hspace{1em}(3.27)}$$

$❑$ 随机梯度下降

梯度下降是通过 $J(w)$ 对 $w$ 的一阶导数来找下降方向，并且以迭代的方式来更新参数，更新方式为 :
$$\begin{array}{c}{g}_i=\frac{\partial J(w)}{\partial w_i}=\left(p\left(x_i\right)-y_i\right)x_i\\ w_i^{k+1}=w_i^k-\alpha g_i\end{array}\text{\hspace{1em}(3.28)}$$

其中 $k$ 为迭代次数。每次更新参数后，可以通过比较 $\Vert J\left(w^{k+1}\right)-J\left(w^k\right)\Vert$ 小于阈值或者到达最大迭代次数来停止迭代。

$❑$ 牛顿法

牛顿法的基本思路是，在现有极小点估计值的附近对 $f(x)$ 做二阶泰勒展开，进而找到极小点的下一个估计值。假设 $w^k$ 为当前的极小值估计值，那么有：
$$\phi (w)=J\left(w^k\right)+J^{\prime }\left(w^k\right)\left(w-w^k\right)+\frac{1}{2}{J}^{\prime \prime }\left(w^k\right){\left(w-w^k\right)}^2\text{\hspace{1em}(3.29)}$$

然后令${\phi }^{\prime }(w)=0$，得到了$w^{k+1}=w^k-\frac{J^{\prime }\left(w^k\right)}{J^{\prime \prime }\left(w^k\right)}$​ 。

因此有迭代更新式：
$$w^{k+1}=w^k-\frac{J^{\prime }\left(w^k\right)}{J^{\prime \prime }\left(w^k\right)}=w^k-H_k^{-1}\cdot g_k\text{\hspace{1em}(3.30)}$$
其中 $H_k^{-1}$​ 为海森矩阵：
$$H_{mn}=\frac{{\partial }^{2}J(w)}{\partial w_m\partial w_n}=h_w\left(x^{(i)}\right)\left(1-p_w\left(x^{(i)}\right)\right)x_m^{(i)}{x}_n^{(i)}\text{\hspace{1em}(3.31)}$$

我们知道牛顿法需要目标函数是二阶连续可微的，这里的 $J(w)$ 显然是符合要求的。

更多关于随机梯度下降算法以及牛顿法的内容，以及逻辑回归算法的正则化等我们将在 第 7 章 过拟合、优化算法与参数优化 中进行讨论。

受篇幅所限，3.3 信息论基础、3.4 Softmax 回归、3.5 Softmax 回归与逻辑回归的关系、3.6 面试问题集锦、3.7 参考资料 详见 一文让你完全弄懂信息论基础 与 softmax 回归实战《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础（下）

参考资料

[1] 《2021春机器学习课程》李宏毅

https://speech.ee.ntu.edu.tw/~hylee/ml/2021-spring.html

[2]《TensorFlow深度学习》（龙龙老师）

https://github.com/dragen1860/Deep-Learning-with-TensorFlow-book

[3] Coursera吴恩达《神经网络与深度学习》

https://www.deeplearning.ai/

[4] 《动手学深度学习》第二版

https://zh-v2.d2l.ai/

[5] 《深度学习》（花书）

https://github.com/exacity/deeplearningbook-chinese

[6] relu函数为分段线性函数，为什么会增加非线性元素

https://www.cnblogs.com/lzida9223/p/10972783.html

[7] 【机器学习】神经网络-激活函数-面面观(Activation Function)

https://blog.csdn.net/cyh_24/article/details/50593400

[8] Logistic Regression (LR) 详解与更多相关的面试问题

https://blog.csdn.net/songbinxu/article/details/79633790

[9] 【机器学习】逻辑回归（非常详细）

https://zhuanlan.zhihu.com/p/74874291

[10] softmax回归(Softmax Regression)

https://blog.csdn.net/u012328159/article/details/72155874

[11] 逻辑回归算法原理及用于解决多分类问题

https://blog.csdn.net/AIHUBEI/article/details/104301492

[12] 逻辑回归（Logistic Regression）（二）

https://zhuanlan.zhihu.com/p/28415991

[13] 数学基础_4——信息论

https://blog.csdn.net/CesareBorgia/article/details/120817481

[14] 信息论（1）——熵、互信息、相对熵

https://zhuanlan.zhihu.com/p/36192699

[15] 一文读懂机器学习分类算法（附图文详解）

https://zhuanlan.zhihu.com/p/82114104

[16] An in-depth guide to supervised machine learning classification

https://builtin.com/data-science/supervised-machine-learning-classification

---

谢谢！

  

转载请注明出处：https://fanfansann.blog.csdn.net/
版权声明：本文为 CSDN 博主 「繁凡さん」（博客），知乎答主 「繁凡」（专栏），Github 「fanfansann」（全部源码），微信公众号 「繁凡的小岛来信」（文章 P D F 版））的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。