Java中方法的概念以及递归的讨论
Java中方法的概念以及递归(汉诺塔问题)
文章目录
- Java中方法的概念以及递归(汉诺塔问题)
-
- 一、方法的基本使用
-
- 1、方法的概念
- 2、实参形参的关系
- 二、方法的重载
-
- 1、重载所能解决的问题
- 三、递归的概念
-
- 1、递归的概念
- 2、递归的练习
-
- 1)、汉诺塔问题
- 2)、青蛙跳台阶
- 3)、青蛙跳台阶(进阶)(递归->动态规划)

一、方法的基本使用
1、方法的概念
Java语言中的“方法”(Method)在其他语言当中也可能被称为“函数”(Function)。
对于一些复杂的代码逻辑,如果希望重复使用这些代码,并且做到“随时任意使用”,那么就可以将这些代码放在一个大括号“{}”当中,并且起一个名字。使用代码的时候,直接找到名字调用即可。
方法存在的意义:
- 能够使代码模块化,使代码的结构更加清晰。
- 当重复使用一个功能(代码)时,只需要写出方法名进行调用,避免相同代码重复累赘。
- 让代码更好理解更简单。
接下来看方法的结构:
访问修饰限定符:自由选择,告诉编译器如何调用该方法。定义了该方法的访问类型。
**静态static:**当调用的主函数是static时,被调用的函数需要为static的。例如:java中,main方法直接调用add方法。此时的add方法需要static修饰。
返回值类型 :方法可能会返回值。return Value Type 是方法返回值的数据类型。有些方法执行所需的操作,但没有返回值。在这种情况下,return Value Type 是关键字void。
参数类型:参数像是一个占位符。当方法被调用时,传递值给参数。这个值被称为实参或变量。参数列表是指方法的参数类型、顺序和参数的个数。参数是可选的,方法可以不包含任何参数。
方法名(函数名):是方法的实际名称。方法名和参数表共同构成方法签名。
方法体:方法体包含具体的语句,定义该方法的功能。
public class Main {
public static void main(String[] args) {
int a = 10;
int b = 20;
int c = add(a, b); //在main方法中,直接调用其他方法,必须为static的方法
}
public static int add(int num1, int num2) {
return num1 + num2;
}
}
2、实参形参的关系
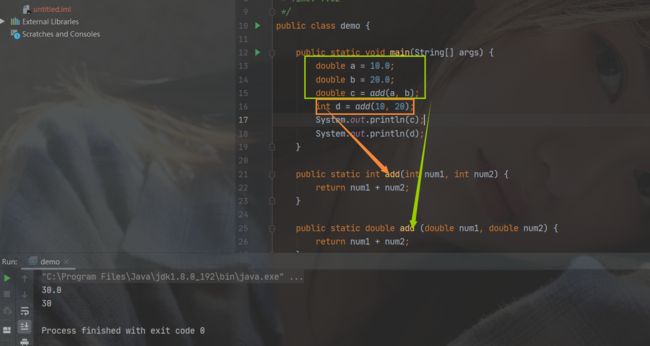
实参:在方法中,实际传递的数值就是实际参数。比如上面的main函数中, int c = add(a, b); 这里的a和b就是实际参数,称为实参。
形参:在被调用的方法里,由实参传递过来的数值,就称为形式参数。形参是实参的一份临时拷贝。也就是说,main函数传递的a和b,与add方法中的a和b,虽然都是10和20(上面代码中),但是二者并不是来自同一块内存空间:如下图所示:
二、方法的重载
1、重载所能解决的问题
在我们平常写代码中,少不了数据的加减乘除。也少不了对不同类型的数据进行四则运算。假设:我们就写了上面的代码(add方法),我们用浮点数(小数)调用add方法,会有什么情况发生?
此时大家就会想,我重新写一个double类型的方法不就行了吗。
没错,就是再次写一个double类型的add就行啦。在C语言中,我们写的函数(方法),不能够写重命的。比如,我写两个add的函数。函数名就是叫add。一模一样,在C语言中是不允许的。
但是在java中,这是可以。也就是这节所讲的 方法重载。
根据形参的类型和形参的个数,去寻找被调用的方法。
上面的代码,分别调用了add方法,虽然都叫add。但是形参类型不一样。所以是两个不同的方法。这就叫重载。
重载的规则
- 方法名相同
- 方法的参数不同。(形参类型不同,个数不同)
- 方法的返回值类型不影响重载
注:当方法的方法名相同,参数相同,但返回值类型不同的时候,这不构成重载。
三、递归的概念
1、递归的概念
一个方法在自己调用自己时,就称为“递归”。
当一个大问题,是由若干个小问题,并且这些小问题的解决方法,都是一样的。这样的问题,很大可能就能用递归去解决。
递归相当于数学上的**“数学归纳法**”,有一个起始条件, 然后有一个递推公式
例如,我们求N!
起始条件: N= 1的时候, N!为1. 这个起始条件相当于递归的结束条件.
递归公式:求N!,直接不好求,可以把问题转换成N!=> N * (N-1)!
例如代码:
public class Main {
public static void main(String[] args) {
int n = 5; //求5的阶乘
System.out.println(fact(n));
}
public static int fact (int n) {
if (n == 1) { //递归结束的条件
return 1;
}
return n * fact(n - 1); //例如5! = 5 * 4! -》 5 * 4 * 3! ,一直递归到1的阶乘,就结束
}
}
2、递归的练习
1)、汉诺塔问题
汉诺塔游戏(7K7K小游戏链接)。在开始讲解之前,大家还是先去玩一玩汉诺塔游戏,看看是什么规则。更容易的理解下面的代码。
牛客网OJ题链接
汉诺塔游戏规则:
现有三根柱子,我们分别叫 left, mid,right。现在有3个圆盘left柱子上,3个圆盘的大小关系为:从上往下,圆盘越来越大。
每次只能取出一个圆盘,并且圆盘在取和放的时候,必须在这三根柱子上完成。不能取出来放到其他地方。
且,大的圆盘不能放到小的圆盘上。
问,怎么移动圆盘,让圆盘从left柱子,移动到right柱子上。
情况一:我们先从1个圆盘举例说明, 我们直接从left柱,移动到right柱即可
情况二: 2个圆盘的情况
情况三: 3个圆盘的情况
这就是大致的思路:
- 先将N - 1层移动到mid柱子,给最下面那一层让路。
- N - 1层移开之后,路就让出来了。此时移动第N层圆盘即可。
- 此时第一步移动的 N- 1层圆盘 还在mid柱子上,现在就是从 mid柱子 移动到 right柱子上。
不要去深究每一步的细节,抓好大致的思路,确定好递归终止的条件。宏观的去想这个问题,就能够很好地抓到问题的本质。
public class Main {
public static void main(String[] args) {
//汉诺塔
int n = 3;
hanoiTower(n, "left", "right", "mid");
}
public static void hanoiTower(int n, String from, String to, String mid) {
if (n == 1) {
System.out.println("move 1 from " + from + " to " + to);
return; //记得返回,终止递归
}
hanoiTower(n - 1, from, mid, to); //图1 -> 图2
System.out.println("move " + n + " from " + from + " to " + to); //图2 -> 图3
hanoiTower(n - 1, mid, to, from); //图3 -> 图4
}
}
2)、青蛙跳台阶
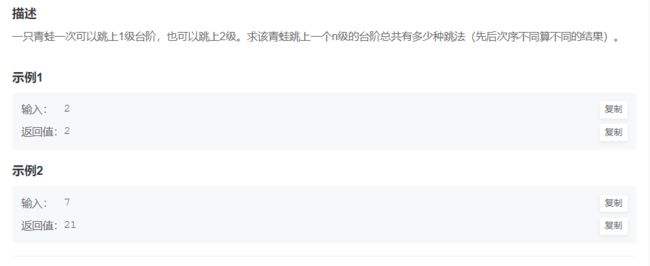
青蛙跳台阶 OJ题链接
情况一:一步台阶 只能跳一次,就跳完了; 1种
情况二:两步台阶 题意是,青蛙一次可以跳一步台阶,也可以跳两步台阶。所以情况二的跳法是 2 种
情况三:三步台阶
现在摆在我面前的问题就是。我要么跳一步台阶。我要么跳两步台阶。
不对,是摆在青蛙面前的问题!!!口误口误!
假设1:青蛙跳一步台阶后,还剩两个台阶没跳。此时是不是又回到了两层台阶的决策问题(上文情况二);
假设2:青蛙跳两步台阶后,还剩一个台阶没跳。此时是不是又回到了一层台阶的决策问题(上文情况一);
我们把这两种情况的假设,结果加起来,就是三层台阶的所有跳法了!!!
再往下,四层、五层……,推导的思路,不就展开了嘛
public class Main {
public static void main(String[] args) {
int n = 3; //台阶数
System.out.println(jumpFloor(n));
}
public int jumpFloor(int target) {
if (target == 1) { //情况一
return 1;
}
if (target == 2) { //情况二
return 2;
}
return jumpFloor(target - 1) + jumpFloor(target - 2); //情况三
}
}
3)、青蛙跳台阶(进阶)(递归->动态规划)
青蛙跳台阶(进阶)OJ链接
看完题目,各位有什么感想???
是不是跟初级的,区别不是很大?递归终止的条件还是一步台阶和两步台阶的情况。
情况一和情况二的情况,我们就不说了,跟上文初阶的一模一样。还是1种跳法和2种跳法;我们重点来看一下三层台阶的情况。
情况三: 三层台阶
三层台阶:也就是说青蛙一次可以跳到3层台阶。弹跳力见涨啊!(注意:并不是说,青蛙就一次只能跳3层台阶,题意是(1 ……n层中 ,每一层 它都可以一次跳过)。
假设青蛙一次最大跳三层:
假设一:青蛙第一次跳一层台阶,还剩两个台阶没跳 -> 两层台阶的决策问题。
假设二:青蛙第一次跳两层台阶 ,还剩一个台阶没跳 -> 一层台阶的决策问题。
假设三:青蛙第一次跳三层台阶,没有台阶跳了 -> 0层台阶的决策问题。
那如果是 四层台阶 五层台阶 N层台阶 呢? 那是不是有几层,就有几种假设情况?那就需要相加!!!来看这个题的代码:
public class Main {
public static void main(String[] args) {
int n = 3; //假设就是3层台阶
System.out.println(frogJumpPlus(n));
}
public static int frogJumpPlus(int n) {
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
int res = 1; //当前,需要选择一种的跳法
//此处的for循环,就是去尝试,跳1步、2步、3步……一直跳到n层台阶,将这些情况全部加起来,就是当前的结果
for (int i = 1; i < n; i++) {
res += frogJumpPlus(n - i); //i控制台阶数,每次循环,都减一步台阶。去递归所有的台阶
}
return res;
}
}
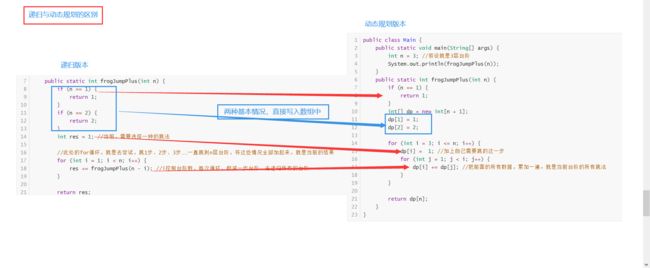
上面的代码,就是经典的递归方式,去解这个题。
其实,在台阶数足够大时,这样的递归,会有很多的重复计算:比如:
计算5层台阶时:
假设一:第一次跳一层台阶,第二次跳一层台阶。此时还剩三层台阶。 -> 三层台阶决策问题。
假设二:第一次跳两层台阶,此时还剩下三层台阶。 -> 三层台阶决策问题。
此时我们就发现了,上面两种假设就会产生重复计算。我们此时就想,有没有一种方法,让我们只计算一次,就能解决重复计算的问题。
那就是加缓存,我们用一块空间,来保存每次计算的结果,当我们需要的时候,直接从内存空间里面拿就行。
暴力递归 -> 动态规划:
public class Main {
public static void main(String[] args) {
int n = 3; //假设就是3层台阶
System.out.println(frogJumpPlus(n));
}
public static int frogJumpPlus(int n) {
if (n == 1) {
return 1;
}
int[] dp = new int[n + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = 1; //加上自己需要跳的这一步
for (int j = 1; j < i; j++) {
dp[i] += dp[j]; //把前面所有数据,累加一遍,就是当前台阶的跳法
}
}
return dp[n];
}
}
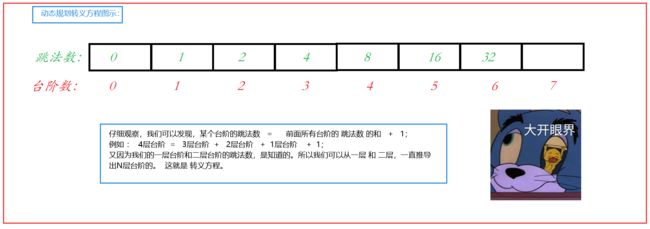
对比两种方法:
我们画出前面几组数据,就能找出规律:
可能你就会疑惑,我写不出来这动态规划。那可以先写递归的版本。在递归的版本上去修改,加缓存。
具体是以什么形式来缓存,还得看你的可变参数,例如这个题的可变参数就只有一个n,也就是台阶数。那我们就开辟一维数组,就能解决。
那如果是两个可变参数,那么此时就可能需要二维数组来做缓存了!!!
总之,像这种考察递归的题目。我们都可以加缓存的形式。到底需不需要加缓存,我们就得看看,递归的时候,是否涉及了大量的重复计算。
最后考考大家,上面写的动态规划的版本,是否还可以优化呢???(提示一下: 两层for循环,时间复杂度O(N2))
好啦,本期更新就到此结束了,我们下期见!!!