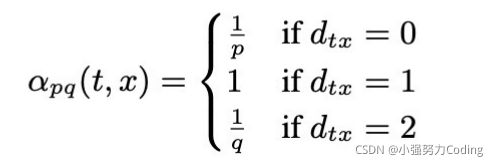Graph Embedding：Node2Vec

参考文章：Alias Method离散分布随机取样 | 天空的城在图的随机游走中，有一块需要随机取样， 比如当前到达v节点，那么下一次随机会到达哪个节点。这种问题其实就是离散分布的随机变量的取样问题。 查了一些资料， 发现Alias Method 是一种很高效的方式。https://shomy.top/2017/05/09/alias-method-sampling/

【Graph Embedding】node2vec:算法原理，实现和应用_浅梦的学习笔记-CSDN博客_node2vec前面介绍过基于DFS邻域的DeepWalk和基于BFS邻域的LINE。node2vec则是一种综合考虑dfs邻域和bfs邻域的graph embedding方法。DeepWalk：算法原理，实现和应用LINE：算法原理，实现和应用简单来说，node2vec是deepwalk的一种扩展，可以看作是结合了dfs和bfs随机游走的deepwalk。nodo2vec 算法原理优化目标设f(u)...https://blog.csdn.net/u012151283/article/details/87081272?spm=1001.2014.3001.5502

参考视频：【图神经网络】GNN从入门到精通_哔哩哔哩_bilibili课程已经更新完毕，PPT，论文，代码在置顶评论下载。结合论文和源码，才能到达最好效果https://www.bilibili.com/video/BV1K5411H7EQ?p=5

Code：

论文链接：

---

DeepWalk可以认为是random walk + skip_gram的模型

random walk本质上是一个DFS（深度优先探索）的过程，丢失了BFS（广度优先探索）的邻居结构信息；而node2vec可以简单的解释为对deepwalk的随机过程优化，综合考虑了DFS和BFS的游走方式，提出了一个biased random walk，训练仍然是skip_gram

node2vec 使用了一个变量a来控制节点的走向，而a是由参数p,q控制的

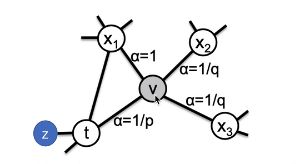
 在上图中，我们已经从 t 节点走到了 V节点。然后我们要，求下一次游走到其他节点的概率，我们定义V节点到下一个节点的概率为，从公式里我们可以看出节点v到节点x的概率  π vx= 上一个节点 t 游走到节点 x 的概率  *  Wvx。Wvx表示节点V到节点x的边的权重大小，这里我着重看一下αpq（t,x）

 我们可以看到α（pq）总共分为三种情况（说明一下，下面的x和上面图中的x1,2,3节点没什么关系，下面的x表示一个未知节点）：

（1）如果距离d(tx) = 0：我们从上面图中可以看到，距离t节点距离为0的节点只有 t 节点本身，或者我们从t节点出发到 x节点 然后再返回到t节点，即（t  - x - t）,那么我们αpq（t,x）的概率此时为为 1/ p，那我们 节点 v 到 节点 t 的概率π vx就为

 （2）如果距离d(tx) = 1:我们从上图中可以看到  ，距离t节点距离为1的节点有z节点和x1节点，也就是说我们t节点游走到v节点之后在走到z和x1节点的概率αpq（t,x）是等于1的，那么我们 节点v到节点x1的概率π vx = ，但是节点v到节点z的概率 = 0，因为节点v和节点z之间没有节点相连接，即Wvz = 0

 （3）如果距离d(tx) = 2:我们从上图中可以看到  ，距离 t节点距离为2的节点有x2节点和x3节点，也就是说我们 t节点 游走到 v节点 之后在走到x2和x3节点的概率αpq（t,x）是等于1 / q 的，那么我们 节点v到节点x2，x3的概率 π vx =

---

 上面我们说了，α是由参数p和q来控制的

• 参数  ：表示节点之间的最短路径，取值为0,1,2

• 参数 p ：返回参数，控制重新采样上一步已访问节点的概率。

  参数p并不直接控制整个游走过程时DFS还是BFS，只控制游走的区域是一直接近起点还是逐渐远离起点
• q：出入参数，控制采样的方向。

  • 当参数 q > 1 时，接下来采样的节点倾向于向  t 靠近，偏向于bfs；

  • 当参数  q < 1时，接下来采样的节点倾向于向  t 远离，偏向于dfs；

 可以发现，当 p = q = 1  时，node2vec就是一个deepwalk模型了

 学习算法

采样完顶点序列后，剩下的步骤就和deepwalk一样了，用word2vec去学习顶点的embedding向量。
值得注意的是node2vecWalk中不再是随机抽取邻接点，而是按概率抽取，node2vec采用了Alias算法进行顶点采样。下面这个链接对Alias的讲解非常通俗易懂
Alias Method离散分布随机取样 | 天空的城在图的随机游走中，有一块需要随机取样， 比如当前到达v节点，那么下一次随机会到达哪个节点。这种问题其实就是离散分布的随机变量的取样问题。 查了一些资料， 发现Alias Method 是一种很高效的方式。https://shomy.top/2017/05/09/alias-method-sampling/

node2vecWalk

通过上面的伪代码可以看到，node2vec和deepwalk非常类似，主要区别在于顶点序列的采样策略不同，所以这里我们主要关注node2vecWalk的实现。

由于采样时需要考虑前面2步访问过的顶点，所以当访问序列中只有1个顶点时，直接使用当前顶点和邻居顶点之间的边权作为采样依据。 当序列多余2个顶点时，使用文章提到的有偏采样。

def node2vec_walk(self, walk_length, start_node):
    G = self.G    
    alias_nodes = self.alias_nodes    
    alias_edges = self.alias_edges
    walk = [start_node]
    while len(walk) < walk_length:        
        cur = walk[-1]        
        cur_nbrs = list(G.neighbors(cur))        
        if len(cur_nbrs) > 0:            
            if len(walk) == 1:                
                walk.append(cur_nbrs[alias_sample(alias_nodes[cur][0], alias_nodes[cur][1])])            
            else:                
                prev = walk[-2]                
                edge = (prev, cur)                
                next_node = cur_nbrs[alias_sample(alias_edges[edge][0],alias_edges[edge][1])]                
                walk.append(next_node)        
        else:            
            break
    return walk

构造采样表

preprocess_transition_probs分别生成alias_nodes和alias_edges，alias_nodes存储着在每个顶点时决定下一次访问其邻接点时需要的alias表（不考虑当前顶点之前访问的顶点）。alias_edges存储着在前一个访问顶点为 t  ，当前顶点为  V时决定下一次访问哪个邻接点时需要的alias表。

get_alias_edge方法返回的是在上一次访问顶点 t  ，当前访问顶点为 v 时到下一个顶点 x 的未归一化转移概率 

def get_alias_edge(self, t, v):
    G = self.G    
    p = self.p    
    q = self.q
    unnormalized_probs = []    
    for x in G.neighbors(v):        
        weight = G[v][x].get('weight', 1.0)# w_vx        
        if x == t:# d_tx == 0            
            unnormalized_probs.append(weight/p)        
        elif G.has_edge(x, t):# d_tx == 1            
            unnormalized_probs.append(weight)        
        else:# d_tx == 2            
            unnormalized_probs.append(weight/q)    
    norm_const = sum(unnormalized_probs)    
    normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]
    return create_alias_table(normalized_probs)

def preprocess_transition_probs(self):
    G = self.G
    alias_nodes = {}    
    for node in G.nodes():        
        unnormalized_probs = [G[node][nbr].get('weight', 1.0) for nbr in G.neighbors(node)]        
        norm_const = sum(unnormalized_probs)        
        normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]                 
        alias_nodes[node] = create_alias_table(normalized_probs)
    alias_edges = {}
    for edge in G.edges():        
        alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
    self.alias_nodes = alias_nodes    
    self.alias_edges = alias_edges
    return

node2vec应用

使用node2vec在wiki数据集上进行节点分类任务和可视化任务。 wiki数据集包含 2,405 个网页和17,981条网页之间的链接关系，以及每个网页的所属类别。 通过简单的超参搜索，这里使用p=0.25,q=4的设置。

本例中的训练，评测和可视化的完整代码在下面的git仓库中，

G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using=nx.DiGraph(),nodetype=None,data=[('weight',int)])

model = Node2Vec(G,walk_length=10,num_walks=80,p=0.25,q=4,workers=1)
model.train(window_size=5,iter=3)    
embeddings = model.get_embeddings()

evaluate_embeddings(embeddings)
plot_embeddings(embeddings)