Ray Tracing - Introduction (L13)
0.Introduction
0.1 光栅化无法处理的问题
Rasterization couldn’t handle global effects well.
1.Soft Shadows(软阴影)
2.light bounces more than once(多次反射)
0.2 Rasterization vs. Ray Tracing
Rasterization
-fast, but low-quality
-real-time
Ray Tracing
-accurate, but very slow
-offline
-~10K CPU core hours to render one frame in production质量和时间为“Trade-off”
1.Recursive (Whitted-Style) Ray Tracing
1.1 Light Rays
基本假设: 直线传播;不发生碰撞;光路可逆
(将物体发射到观察者的光线等效成由观察者发向物体一道“感知光线”,光路仍成立,这也是光线“追踪“的命名由来)
1. Light travels in straight lines (though this is wrong)
2. Light rays do not “collide” with each other if they cross (though this is still wrong)
3. Light rays travel from the light sources to the eye (but the physics is invariant under path reversal - reciprocity[可逆性]).Eyes send out feeling rays to the world
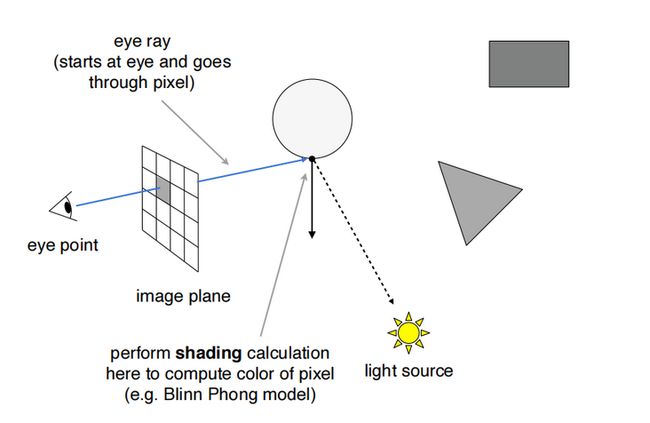
1.2 Ray Casting(光线投射:生成不同的光线)
1.2.1 概述
基本流程:
1. Generate an image by casting one ray per pixel
2. Check for shadows by sending a ray to the light1.2 2 An Example:
Assumptions
1.光源为点光源,眼睛为针孔摄像机(即忽略光源和相机的大小和尺寸)Step 1
Step 2
基本步骤:
1.对于每个像素,与眼睛连线形成Ray,计算这条光线照亮的场景中最近的点
2.该点与光源连线[这条连线叫做Shadow Ray],判定是否被照亮以及计算颜色
3.将计算结果写回原像素1.2.3 Recursive Ray Casting(Whitted-Style) 概述
模拟光线不断弹射的过程,将多次反射和折射的结果都加入到该点的像素值上。
注意:多次反射和折射当然要考虑能量衰减。
效果图
1.3 Ray-surface Intersection
1.3.1 Ray Equation
Ray is defined by its origin and a direction vector.
$$ \vec{r}(t)=\vec{o}+t\vec{d}(0\leq t<\infty) $$
ATTENTION:图形学中一般不纠结边界条件(如t>0还是t>=0)
Example: Ray Intersection With Sphere
$$ Ray:\vec{r}(t)=\vec{o}+t\vec{d}(0\leq t<\infty)\\ Sphere:(\vec{p}-\vec{c})^2-R^2=0\\ Solve\space for\space intersection:(\vec{o}+t\vec{d}-\vec{c})^2-R^2=0 $$
最后可以化为二次方程进行求解,注意根据光线与球面的位置关系分类讨论。
1.3.2 For implicit surface
$$ General\space implicit\space surface:f(\vec{p})=0\\ Substitute\space ray\space equation:f(\vec{o}+t\vec{d})=0\\ [Solve\space for\space positive\space roots.] $$
1.3.3 For Triangle Mesh(Explicit surfaces)
(作为显式表示的最重要代表,选用三角形面)
[Point in polygon Test]
检查一点是否在多边形之内,可作一射线从该点开始往任意方向投射,如果射线与多边形边的交点个数为奇数,则该点位于多边形内部。
但是直接按此方法判定光线和三角形面的位置关系计算量过大。
改进:问题转化为求出光线和三角形所在平面的交点,再判断交点是否在三角形内部。
示意
定义平面:法线+平面上任意一点P'
$$ Plane\space Equation:(\vec{p}-\vec{p'})\cdot \vec{N}=0\\ 可以写成\space ax+by+cz+d=0 $$
至此已经可以解出光线与平面的交点,再判定是否在三角形内部。
改进:(可以直接解出光线和三角形的交点,并验证其解的合理性)
重心坐标均非负,则交点在三角形内
1.4 Accelerating Ray-Surface Intersection
在像素数过多、光线弹射情况复杂时,上述方法效率过低。
San Miguel Scene(经典场景), 10.7M triangles
1.4.1 Bounding Volumes
引入”包围盒“Bounding Volumes,即光线如果不会碰到Bounding Volumes,则它一定不会碰到物体。
对于Bounding Volumes的进一步定义:Bounding Box is the intersection of 3 pairs of slabs
即:包围盒是三组平面的交集。
常用包围盒:Axis-Aligned Bounding Box(AABB,轴对齐包围盒)
1.4.2 Ray Intersection with AABB
KEY ideas
The ray enters the box only when it enters all pairs of slabs
The ray exits the box as long as it exits any pair of slabs即:进入任何一对平面即认为进入box,离开所有平面才认为离开box。
因此对于每一对平面计算$t_{min}$和$t_{max}$,求出进入时间和离开时间:
$$ For\space 3D\space box,\\ t_{enter}=max\{t_{min}\}\\t_{exit}=min\{t_{max}\}\\ $$
再考虑由于光线实际为射线带来的正负号问题。
$$ 若t_{exit}<0,\space则box在光线后方\Rightarrow无交点\\ 若t_{exit}\geq0,t_{enter}<0,\space则光线起点位于box内部\Rightarrow有交点 $$
综上,得到结论:
$$ Ray\space and\space AABB\space intersect\space iff (if\space and\space only\space if)\\ t_{enter} 因为计算更方便。1.4.3 Why Axis-Aligned?