彻底学会这个案例，Processing生成艺术再也难不倒你。Processing 案例教学 — 立方矩阵

今天我们来一起学习这个案例吧：

立方矩阵

完成这个案例大体分为4个步骤：

1. 在正交视角下绘制一系列的正方体
2. 将box指令替换为单独画正方体的每个矩形面的方式，从而控制每个面的图案
3. 编排正方体的旋转动作，并给他们的旋转加入一点时间差
4. 让每个正方形的样式略有不同

---

I. 在正交视角下绘制一系列的正方体

首先我们来学习一下关于正交视角的知识

---

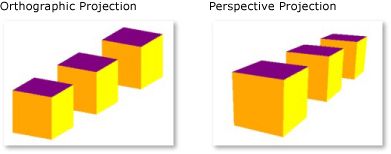
正交视角下3d坐标系呈现一种2.5D的效果。相比于透视（perspective）呈现出的近大远小，在正交视角下，相同大小的物体在不同距离上看起来是一样的。拿游戏来举例：魔兽世界是透视视角，而魔兽争霸是正交视角。

正交 vs 透视

在processing中使用正交视角可以使用以下指令：

ortho(left, right, bottom, top, near, far)

其中 left, right, bottom, top 分别代表相机的左右上下边界，near, far代表远近截距。6个参数定义了一个虚拟空间的立方体空间，我们绘制的物体落在这个空间内的部分才会被看到。

参考Processing官方ortho示例

---

让我们开始写代码吧：

首先，在setup函数中设置渲染模式为P3D，并创建一个正交相机

void setup() {
  // 设置画布大小为 430, 420 且渲染模式为P3D
  size(430, 420, P3D);
  // 针对RetinaDisplay高像素密度的优化 
  pixelDensity(displayDensity());

  // 设置3d相机为正交相机
  ortho(-width/2, width/2, -height/2, height/2); 
}

至此我们创建了一个正交相机，其左边界为-width/2，右边界为width/2，上边界为-height/2，下边界为 height/2。width和height是窗口的宽度和高度，在这个程序里分别为430，420。

下一步，我们在draw函数中开始画立方体

void setup(){
  ...
}
void draw(){
  // 每一帧开始时把画布清空成黑色背景 
  // (括号里为灰度值，0是纯黑255是纯白，中间是灰色)
  background(0);
  
  // 在当前坐标下，画一个大小为20的立方体
  box(200);
}

运行效果如下

运行效果1

我们发现在左上角有一个白色方块，那个正是我们使用box画出来的方块。显然，他的位置不对。我们需要改变它的绘画位置。

对于3D图形元素，我们不再能像2D元素（rect, ellipse等）一样在指令中直接指定其画图的位置，而是需要通过坐标系变换来改变它的画图位置。

坐标系变换的顺序一般是先平移(translate)，然后旋转(rotate)，最后缩放(scale)。

需要注意的是，我们当前的坐标原点(0,0,0)并不在屏幕的正中央，而是在屏幕左上角的位置，我们先做一个translate(width/2, height/2)，即可把坐标系移动到屏幕中央。之后再使用box指令画图，即可看到正方体移动到屏幕中心了。

void setup(){
 ...
}
void draw(){
 ...
 
 // 移动坐标系至屏幕中央
 translate(width/2, height/2);
 // 在当前坐标下，画一个大小为20的立方体
 box(200);
}

运行效果如下

运行效果2

目前立方体看起来就是一个正方形，因为它的一个面正对着摄像机。接下来我们把它做一些旋转，让它有一个立体的感觉。

---

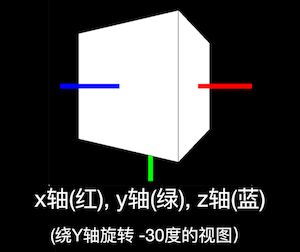
我们来复习一下坐标轴旋转的相关知识

3D绘图中旋转相关的指令有3个，分别是rotateX(angle), rotateY(angle), rotateZ(angle)。他们的工作方式类似，其中XYZ代表旋转围绕的坐标轴，而括号内的参数代表旋转的角度。角度按当某个坐标轴正对你时的顺时针方向来测定，单位为弧度radians。

xyz轴示意图.png

rotateX、rotateY、rotateZ旋转正方向的示意图.gif

---

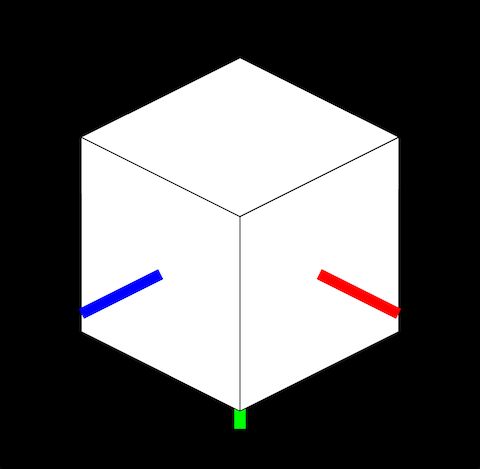
为了把正方形变成下面的样子，我们需要让正方形做一些旋转。可以在box(200)指令前加一些坐标轴旋转的指令。

大家猜猜看需要旋转哪几个轴，又需要各旋转多少度？

看起来像几个2D菱形构成的3D立方体

答案：旋转x轴-30度，旋转y轴-45度

void setup(){
  ...
}
void draw(){
  ...
 
  // 移动坐标系至屏幕中央
  translate(width/2, height/2);
  // 旋转-30度，等于 -pi/6
  rotateX(-PI/6);
  // 旋转-45度，等于 -pi/4
  rotateY(-PI/4);
  // 在当前坐标下，画一个大小为20的立方体
  box(200);
}

运行效果3: 旋转后的立方体，注意对比三个坐标轴现在的位置

至此，我们完成了单个立方体的绘制。

下一步，我们使用循环将立方体分别画在空间的不同地方。

---

我们首先来规划一下我们的网格。

立方矩阵

参考原图，我们发现空间中的立方体个数是15x15个。对比每个立方体的坐标，我们可以发现他们的z坐标是相同的，只是x、y坐标分布在一个网格上。而由于相邻两个立方体之间的间隔相同，他们的x、y坐标可以用两个等差数列来分别表示。

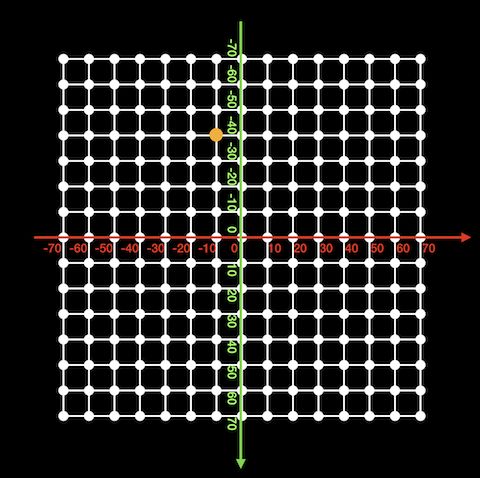
以10像素为间隔为例，可以构建如下坐标系，其中每个圆点上可以放置一个立方体。

按照间隔为10来构建的坐标系

我们一般以 i, j 来标记二维矩阵中的每个点，i 代表横轴上的序号，也就是列号；而 j 代表竖轴上的序号，也就是行号；并且序号是从0开始；所以i = 5, j = 3代表第6行第4列的那个点(上图黄点)。

我们来做一下计算
i=0, j = 0 -> x= -70, y = -70
i=1, j = 0 -> x= -70 + 10, y = -70
i=1, j = 1 -> x= -70 + 10, y = -70 + 10
i=2, j = 0 -> x= -70 + 20, y = -70
i=2, j = 1 -> x= -70 + 20, y = -70 + 10
i=2, j = 2 -> x= -70 + 20, y = -70 + 20
......

我们发现

x = -70 + i * 10
y = -70 + j * 10

更近一步的说，假设N是每行/列的点的数量，D是间隔的距离

左边界/上边界的坐标 = -(N-1)/2 * D = -70
x = -(N-1)/2 * D + i * D = -70 + i * 10
y = -(N-1)/2 * D + j * D = -70 + j * 10

我们只需要让 i 和 j 分别依次等于0,1,2,3,...14即可得到所有的坐标值，写成代码即为

for(int j = 0 ; j < 15 ; j++){
    for(int i = 0 ; i < 15 ; i++){
        float x = -70 + i * 10;
        float y = -70 + j * 10;
    }
}

---

完成坐标的计算以后，我们需要:

1. 将坐标轴从目前的位置（画布中央）依次移动到每一个(x , y)坐标上
2. 旋转合适的角度
3. 绘制正方体
4. 将坐标轴移动回画布的中央

需要注意的是，我们目前的位置已经是经过一次translate(width/2 , height/2)之后所得到的。后续的平移是叠加在先前的平移之上的。

关于使用pushMatrix()和popMatrix()来管理叠加的坐标系: pushMatrix()和popMatrix()必须成对使用；从pushMatrix()到popMatrix()之间的坐标系变换在使用popMatrix()指令后被撤销，使程序的当前坐标系恢复到使用pushMatrix()之前的状态。

在对每个单独的立方体进行坐标系变换前，我们可以使用pushMatrix来保存当前的坐标系；等绘制完box以后，使用popMatrix来撤销针对于这个立方体所做的所有坐标系变换，从而回到push之前的坐标系。

针对于每个立方体的代码即为：

...
//  保存当前的坐标系
pushMatrix();
//  1. 将坐标轴从目前的位置（画布中央）依次移动到每一个(x , y)坐标上
translate(x,y);
//  2. 旋转合适的角度
rotateX(-PI/6);
rotateY(-PI/4);
//  3. 绘制正方体
box(5);
// 4. 将坐标轴移动回画布的中央
popMatrix();

将这些代码放到循环中：

for (int j = 0; j < 15; j++) {
  for (int i = 0; i < 15; i++) {
    float x = -70 + i * 10;
    float y = -70 + j * 10;
    // 保存当前的坐标系
    pushMatrix();
    // 1. 将坐标轴从目前的位置（画布中央）依次移动(translate)到每一个(x, y)坐标上
    translate(x, y);
    // 2. 旋转合适的角度
    rotateX(-PI/6);
    rotateY(-PI/4);
    // 3. 绘制正方体。
    box(5);
    // 4. 将坐标轴移动回画布的中央
    popMatrix();
  }
}

用它来替换之前单个立方体的绘图代码部分：

void setup() {
  ...
}

void draw() {
  ...
  
  // 移动坐标系至屏幕中央
  translate(width/2, height/2);
  ======= 以下部分被替换 =======
  // 旋转-30度，等于 -pi/6
  //rotateX(-PI/6);
  // 旋转-45度，等于 -pi/4
  //rotateY(-PI/4);
  // 在当前坐标下，画一个大小为20的立方体
  //box(200);
  =============================
  for (int j = 0; j < 15; j++) {
    for (int i = 0; i < 15; i++) {
      float x = -70 + i * 10;
      float y = -70 + j * 10;
      // 保存当前的坐标系
      pushMatrix();
      // 1. 将坐标轴从目前的位置（画布中央）依次移动(translate)到每一个(x, y)坐标上
      translate(x, y);
      // 2. 旋转合适的角度
      rotateX(-PI/6);
      rotateY(-PI/4);
      // 3. 绘制正方体。
      box(5);
      // 4. 将坐标轴移动回画布的中央
      popMatrix();
    }
  }
}

运行效果4：15x15立方体矩阵

至此，我们完成了第一个步骤，绘制一个立方体矩阵。

为自己鼓鼓掌吧，你已经完成了最基础最重要的一步了！