＜＜从零入门机器学习＞＞之线性回归-房价预测问题

1. 学习前需要掌握的知识以及问题背景

1.1 学习知识背景

       学习本实战例子前提需要掌握机器学习中线性回归的概念，Python的基础语法，MSE，R2_score等变量的含义，以及数学求解过程，本篇博客默认是基于掌握如上知识点进行的。

1.2 房价预测问题以及本实战的原始数据(usa_housing_price.csv文件放在文章的末尾，自行取)

        如下是usa_housing_price.csv文件的部分数据截图，可见像Area Income、House Age、等属性都会影响到区域内的Price。

        现在基于usa_housing_price.csv数据，建立线性回归模型，预测合理房价。主要预测问题分为三个步骤，如下所示：
        1. 以面积为输入量，建立单因子模型，评估模型表现，可视化线性回归预测结果。
        2. 以income、house_age、number of rooms、population、area为输入变量，建立多因子模型，评估模型表现。
       3. 预测Income=65000、House Age=5、Numbers of Rooms=5、Population=30000、size=200的合理房价。

2. 根据具体步骤解决问题

2.1 以面积为输入量，建立单因子模型，评估模型表现，可视化线性回归预测结果

        2.1.1 将usa_housing_price.csv文件通过pandas的read_csv(path)方法读取到内存中来，然后通过head()方法查看文件的部分内容特征，如下代码和图所示：

        注意read_csv方法当中的path是存放usa_housing_price.csv文件的本地路径，每个人存放的路径都不同，可以自定义。

import pandas as pd
import numpy as np
data = pd.read_csv('D:/Google/picture/usa_housing_price.csv')
data.head()

        data.head()方法显示出的内容和我们表格的表头内容格式一致，只不过其只显示源文件内容的一部分

        2.1.2 引入matplotlib包将每个影响因子和Price结合起来绘制关系图（其中Price作为y轴、其余影响因子分别作为x轴）：

from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10)) 
fig1 = plt.subplot(231) #两行三列第一幅图(两行三列：x走两个单元格,y走三个单元格),下同
plt.scatter(data.loc[:,'Avg. Area Income'],data.loc[:,'Price'])  #plt.scatter(x,y) 花点图 (下同)
plt.title('Price VS Income')
fig2 = plt.subplot(232) 
plt.scatter(data.loc[:,'Avg. Area House Age'],data.loc[:,'Price'])  
plt.title('Price VS Age')
fig3 = plt.subplot(233) 
plt.scatter(data.loc[:,'Avg. Area Number of Rooms'],data.loc[:,'Price']) 
plt.title('Price VS Rooms')
fig4 = plt.subplot(234) 
plt.scatter(data.loc[:,'Area Population'],data.loc[:,'Price'])  
plt.title('Price VS Population')
fig5 = plt.subplot(235) 
plt.scatter(data.loc[:,'size'],data.loc[:,'Price'])  #plt.scatter(x,y)
plt.title('Price VS size')
plt.show()

        2.1.3 将面积因子size作为x、对应的房屋价格Price作为y，调用 sklearn包的相关方法训练线性回归模型。接下来，再以size作为输入变量，预测Price的值，并以MSE和R2_score的值来评估单因子模型：

        定义x、y，训练出线性回归模型，而且以size作为x，通过已训练出的模型，预测y的值并打印输出出来：

#define x and y
x = data.loc[:,'size']
y = data.loc[:,'Price']
x = np.array(x).reshape(-1,1) #需要将x转换成一维的数组
#set up the linear regression model
from sklearn.linear_model import LinearRegression
LR1 = LinearRegression()
LR1.fit(x,y)
y_predict_1 = LR1.predict(x)
print(y_predict_1)

y_predict的值：

        通过预测出来的y_predict的值来评估线性回归模型的表现，其中主要是通过MSE以及R2_score来作为判别的标准(MSE的值越小越好，R2_score的值越接近1越好)：

#evaluate the model
from sklearn.metrics import mean_squared_error,r2_score
mean_squared_error_1 = mean_squared_error(y,y_predict_1) #MSE
r2_score_1 = r2_score(y,y_predict_1) 
print(mean_squared_error_1,r2_score_1)

MSE和R2_score的值：

        将源数据的size作为x、Price作为y画出散点图，预测出来的y_predict_1作为y画出直线图（斜率k越接近1越好）：

fig6 = plt.figure(figsize=(8,5))
plt.scatter(x,y) #画点图
plt.plot(x,y_predict_1,'r') #画直线图 r->代表红色
plt.show()

2.2 以income、house_age、number of rooms、population、area为输入变量，建立多因子模型，评估模型表现。

        以income、house_age等多变量的因子作为x，Price依旧做y，重复单因子上面的操作，通过源数据训练模型，并以多因子x作为输入变量，预测y的值，并通过MSE和R2_score评估模型：

#define x_multi 多因子(除掉price)
x_multi = data.drop(['Price'],axis = 1)  #data的列去掉Price
x_multi.head()
#set up 2nd linear model
LR_multi = LinearRegression()
#train the model
LR_multi.fit(x_multi,y)
y_predict_multi = LR_multi.predict(x_multi)
print(y_predict_multi)
mean_squared_error_multi = mean_squared_error(y,y_predict_multi) #MSE
r2_score_multi = r2_score(y,y_predict_multi) 
print(mean_squared_error_multi,r2_score_multi)
fig7 = plt.figure(figsize=(8,5))#将y和y_predict_multi画散点图 (接近直线 k=1(k:斜率))
plt.scatter(y,y_predict_multi)
plt.show()

将y和y_predict_multi画散点图 (接近直线 k=1(k:斜率)越好)

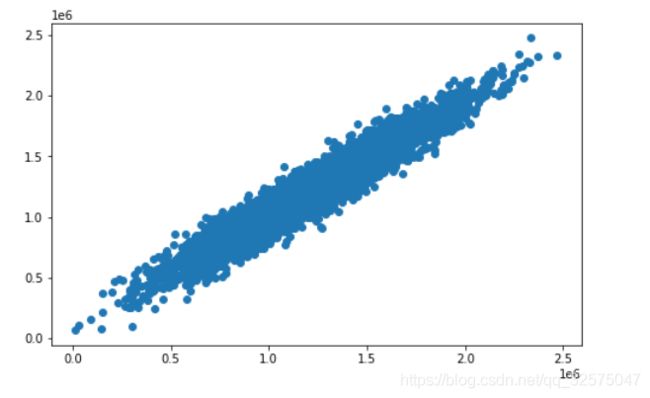
       多因子的MSE和R2_score值为：其MSE较单因子模型下降了很多倍数，R2_score的值也越来越接近1了，证明多因子的线性回归模型比单因子模型更加好，侧面反应出房屋价格Price应该由多个因子影响：

3. 预测Income=65000、House Age=5、Numbers of Rooms=5,Population=30000、size=200的合理房价

        通过第二个步骤我们已经训练出多因子的线性回归模型，这样我们把上面的数据作为输入变量x传到模型中即可得出对应的y值，也就是Price的值：

x_test = [65000,5,5,30000,200]
x_test = np.array(x_test).reshape(1,-1)
y_test_predict = LR_multi.predict(x_test)
print(y_test_predict)

        需要注意到的是predict方法接收到的参数是数组不是列表，我们需要将其格式进行转换一哈，如下是我们预测的房价信息：

        如下是本篇博客源数据usa_housing_price.csv文件，大家自行获取（提取码：1234）
usa_housing_price.csv