- 自顶向下的归并排序
1.不断二分->log2n
// 递归使用归并排序,对arr[l...r]的范围进行排序
template
void __mergeSort(T arr[], int l, int r){
if (l >= r)
return;
int mid = (l + r) / 2;
__mergeSort(arr, l, mid);
__mergeSort(arr, mid + 1, r);
__merge(arr, l, mid, r);
}
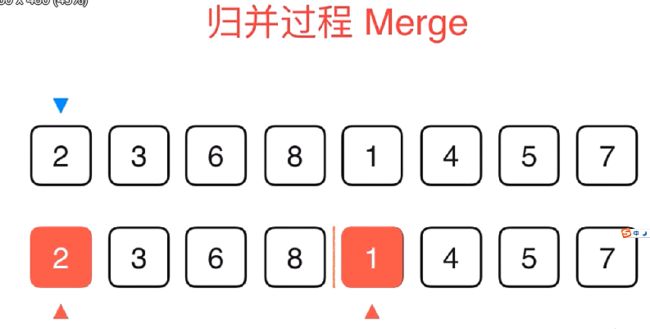
2.排序归并->n
image.png
比较两边,逐个填入
// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
template
void __merge(T arr[], int l, int mid, int r){
T *aux = new T[r - l + 1];
for (int i = l; i <= r; i++)
aux[i - l] = arr[i];
// 初始化,i指向左半部分的起始索引位置l;j指向右半部分起始索引位置mid+1
int i = l, j = mid + 1;
for (int k = l; k <= r; k++){
if (i > mid){ // 如果左半部分元素已经全部处理完毕
arr[k] = aux[j - l]; j++;
}
else if (j > r){ // 如果右半部分元素已经全部处理完毕
arr[k] = aux[i - l]; i++;
}
else if (aux[i - l] < aux[j - l]) { // 左半部分所指元素 < 右半部分所指元素
arr[k] = aux[i - l]; i++;
}
else{ // 左半部分所指元素 >= 右半部分所指元素
arr[k] = aux[j - l]; j++;
}
}
delete[] aux;
}
3.小数目排序有序可能性更大,用插入排序是更好的选择
- l,r版的插入排序
template
void insertionSort2(T arr[], int l, int r){
for (int i = l + 1; i <= r; i++){
T e = arr[i];
int j;
for (j = i; j > l&&arr[j - 1] > arr[j]; j--){
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}
- 改进的第二版归并算法
template
void __mergeSort2(T arr[], int l, int r){
// 优化2: 对于小规模数组, 使用插入排序,一是因为此时数组近乎有序的概率会比较大
//二是因为 N^2 和 NlogN 前是有常数的系数的,对于这个系数,插入排序比归并排序小
//所以当N小到一定程度时,插入排序会比归并排序快一些
if (r - l <= 15){
insertionSort2(arr, l, r);
return;
}
int mid = (l + r) / 2;
__mergeSort2(arr, l, mid);
__mergeSort2(arr, mid + 1, r);
// 优化1: 对于arr[mid] <= arr[mid+1]的情况
//因为l到mid,mid+1到r已经有序了,不用merge
// 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
if (arr[mid] > arr[mid + 1])
__merge(arr, l, mid, r);
}
- 自底向上归并排序
无优化版本:
template
void mergeSortBU(T arr[], int n){
//对进行merge的元素个数进行遍历
//第一轮归并排序,每一次只看一个元素,之后每次看2、4、8个元素
for (int size = 1; size <= n; size = size * 2;)
//具体每一轮归并的过程中,起始的元素位置
//第一轮从(0,size-1)、(size,size*2-1)进行一次归并
//第二轮对(size*2,size*3-1)、(size*3,size*4-1)进行一次归并
//每次跨过2个size大小的区域,这2个区域要进行merge操作
for (int i = 0; i + size < n;/*保证第二部分的存在和i+size-1不越界*/ i = i + size * 2)
//对arr[i...i+size-1]和arr[i+size...i+size*2-1]进行归并
__merge(arr, i, i + size - 1, min(i + size + size - 1, n - 1));
//万一后面没有size个元素,即i+size+size-1越界
}
- 加入优化:
template
void mergeSortBU2(T arr[], int n){
for (int i = 0; i < n; i = i + 16)
insertionSort2(arr, i, min((i + 15), n - 1));
for (int size = 16; size <= n; size = size * 2)
for (int i = 0; i + size < n; i = i + size * 2)
if (arr[i + size - 1] > arr[i + size])
__merge(arr, i, i + size - 1, min(n - 1, i + size + size - 1));
}
!!!注意:对两部分而言,第一个元素和最后一个元素在角标上相差的是size-1。
自底向上的归并排序有它特有的优势:
排序过程中没有使用数组[通过索引直接获取元素]的特性,所以其在链表中扮演着重要角色,可以很好的对链表进行O(nlogn)的排序