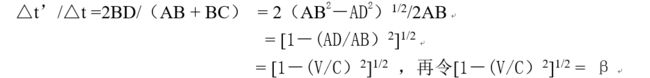"20世纪初, 人类发现了光速是不变的。对于这个不变的刚性事实,撼动了物理大厦的基石。"
——“双生悖论”随笔之七
前文中已经提到,说孪生兄弟“天序”的变化,是与光速不变相关联的,其实,光速不变带来的是物理世界中方方面面的变化。
一、不变与变的哲学
生活中的经验告诉我们,存在着一种“不变与变”的法则:如果有一件事情是刚性的,不能改变的,那么与它相关的许多事情就都要随之发生改变。
科技总是在不断进步,这一不变的法则,随之带来了人类生存状态的不断变化;把保护人类良好的生态环境作为一个谁都不能违反的大法,则人类的行为将随之发生方方面面的相应的变化;每一个人总要吃饭、总是会死,这一不变的法则,随之带来了人们生活态度和生活方式的许多变化;一个家庭为了子女能享受更好的教育,并作为一个不能变更的原则,那么这个家庭的精力投入、资金的支出,甚至父母的工作、居家的位置、卧室的安排都要随之发生变化;今天是2016年3月1日,春天来了,这是不能改变的自然法则,则与它相关的事物都会随之发生变化:气温逐步上升了,室内的暖气要停了,刮的风暖和了,河里的冰融化了,柳树有了新芽,桃树要开花。
光速不变,使得物理世界中许多事情也发生了相应的变化。
下面,就来说说这些变化了的事情。
二、光速不变,运动钟走慢
一只钟,放在高速列车上,就会走慢。刚开始接触这部分内容,很难理解,学了一段,像是理解了,而对一些具体的情形进行分析时,又会犯迷糊。为了能对这个难缠的题目有点兴味,我设计了一场魔术表演,下面介绍这场魔幻般的表演。这是熟悉狭义相对论的魔术师设计的一场表演,这个表演也可以在E城通过合理的设置,可以作为场馆内活动的一项内容。
这场表现是在一个剧场里进行的。
在剧场的入口处,每个观众可领到一只一模一样的钟,观众要用这只钟要来测量这场表演过程所用的时间。
剧场内分上、下两个观众区,观众区的正前方是个大舞台,舞台中央画有一个大大的等边三角形——△ABC,并画出了这个三角形的高BD,D是AC的中点。舞台上的“演员”只有一位,是一个机器人,它的表演就是单调、匀速地在舞台上按规定的线路行走,因此这个表演显然是乏味的、简单的,但其内涵却是深刻的,耐人寻味的。
大幕拉开,表现开始。
上区的观众看到这个机器人是沿着这个等边三角形的高——即BD直线,从D走到B,再从B走到D,这就完成了一个表现的全过程,而下区的观众看到这个机器人是沿着这个等边三角形的一条边从A走到B,再沿着另一条边由B走到C,就完成一个表演的全过程。两个区的观众看到的是同一个“演员”,从开始到结束的表演,而走的却是不同的路线:上区的观众看到“演员”走的是沿着等边三角形的高由下向上再由上向下的一条直线;下区的观众看到的是沿着等边三角形的两个腰,走的是两条斜线。
这位“演员”一开始表演,两区的观众就开始记时;表演结束,两区的观众记时结束。这个表演的一个关键点是,无论是上区或下区的观众,虽然看到的机器人走的路线不同,但这个机器人行走的速率都是一样的,是一个不变的值,因此观众看到的演员行走的距离是与时间成正比的。这样,两个区的观众记录到的时间显然是不会一样的:上区的钟因为“演员”行走的路线短,钟面显示的时间少;下区的钟因为“演员”行走的路线长,钟面显示的时间多。
可以计算一下这个结果。
如果这个等边三角形的每边长为10米,则其高为8.67米,假如机器人的速度是1米/秒。则上区的观众看到机器人走完全程用时是17.3秒,而下区的观众看到机器人走完全程的时间是20秒。上下两区的观众,看到的是同一个“演员”的表演,但是由于他们所在的区域不同,看到的情形就有了区别:上区的观众看到的演员开始与结束是在同一个点D,行走的路线短,用时少;下区的观众看到演员开始与结束是在不同的两个点A、C,用时多。或者说上、下区的观众观看的同一个表演,钟上显示的时间不同,上区的钟走慢了:下区的钟走得快,上区的钟走时1秒,下区的钟要走1.15秒;而下区的钟走1秒,上区的钟只走了0.867秒。因为“演员”的速率对上、下区的观众都一样,因此这里上、下区时间之比,就是这个等边三角形的高与边长之比,时间的变化可以通过空间的几何性质来计算。
好了,魔术表演就完了,我们把这个魔术转化为一个在狭义相对论中的一个典型问题。
这里测量时间是用一只钟,钟总是与时间相关的,因此讨论这个问题,还必须弄清楚时间是什么。
什么是时间?是一个复杂的问题(可参见《时间随笔》),而物理学中所说的时间,大都是指能用钟来进行测量的那个“东西”,钟就是测量这种“东西”的工具。从钟上读出的数字就是时间。
如此看来,为了方便下面的讨论,先要定义一只钟。由发条或电池驱动的钟,含有弹簧、齿轮或电池等器件,太复杂,讨论这里的问题不方便。因此,要定义一只简单的、理想的钟。
这只钟没有机械运动的部件,只有上下平行放置两片平面镜,光束在期间运动,但两镜之间相隔15万公里。制作这只钟显然是不实际的,这是想象中的一只钟。假设一束光从下镜面垂直向上,射向上镜面,又从上镜面垂直反射回到下镜面。我们知道光速是每秒30万公里,镜面的反射是不用时间的,因此,光由下而上,再由上而下,往返一次正好是1秒,光束完成一次这样的运动,就会发出滴答一次响声。光在钟里不断地上下来回运动,钟就滴答滴答地响着。这就是爱因斯坦设计的钟,也称作“光钟”。
假设有一列高速列车,车速为V,由西向东飞驰。
人们在这样的列车的一节车厢里安装了这样的的钟,此钟的两块平行的镜片是分别安装在车厢中间的顶子上和地板上,一束光在这两个平行镜片之间往返一次假定是1 秒。有两位观测者,一位在此高速列车上,一位在车道旁的路基上。他们俩都带着一只结构一样、走时精准的钟在身边。
车厢内,一束光由车厢的下面的镜面上垂直向上射出,再通过上面的平面镜反射回来。如果这束光就是上述魔术表演的那位机器人“演员”,行走的速率不变,是光速 C。列车上观测者和路基上的观测者就相当于上区和下区的观众。类似于上面的分析,就会导致运动的钟走慢的结论。
列车上的观测者看到一束光由下而上,再由上而下,然后就听到了光钟的一声滴答,表示流逝的时间是1秒,光束前端的运动可以用图表示成↑↓,实际是两条重叠的直线(对应魔术表演中的三角形高BD),光束前端开始与结束是在同一个点(D)。
路基上的观测者看到这束光前端是这样运动的:由于列车自西向东运动,光束的前端就出现了光束向上、向东运动的合成,是斜向上方的运动,碰到上面的平面镜后,经反射出现了斜向下方的运动,若用图表示就是↗↘,像人字形的折线(对应魔术表演的三角形的两条边AB与BC),光束的前端开始与结束是在两个不同的点(A与C)。
如此看来,光束上下一次的运动,在列车中、路基上的不同参考系中的观测者看到的是两个不同的图象。
列车上的人看到光束前端上下一次,运动的路线是↑↓,走了30万公里,用了一秒钟;而路基上的人发现光束前端,走了两条斜边↗↘,走的路程大于30万公里。但按照爱因斯坦的公设,无论哪一个参考系光速都一样,都是30万公里每秒。那么,路基的观测者一定会观测到光走完这段人字折线路程(↗↘)所用的时间必然会大于1秒,而列车上的观测者测得这一过程只用了1秒。路基上的观测者必然会认为是车上的钟走慢了。这就从光速不变——即不同惯性系中光都是同一个速率,直接得到一个重要结论:运动的钟走慢了。
按照上面的分析,还可以转化为一个简单的数学习题,一位初中生就可算得车上、车下两只钟的时间相差多大。
设这个等边三角形的高是BD,两条斜边是AB和BC。车上的观测者测得光行时间是△t’= 2BD/c;路基上的观测者测得的光行时间是△t =(AB+BC)/c,由此
式中β是一个纯数因子,是一个总小于1、大于零的数。一个正数乘了它会变小;一个正数被它除,会变大。β决定列车的速度V和光速C。这样就有
△t’=β△t
如果列车是以0.8C的速度飞驰,那么可计算得β=0.6,列车上的光钟的一次滴答声(△t’=1秒),相当于的路基上的钟(△t = △t’/β=1.67)走了1.67秒。
再深入分析,还可以看到,列车上光束上下一次这个事件,是在车上同一个地点发生的(在上述魔术表演中的D点),这同一地点的钟显示一个过程时间最短,称作“原时”;路基上的观察者观察到这个事件是在两个不同地点(在上述魔术表演中是在A、C两点)发生的事件,是路基上对应的两个不同的地点的两只钟记录的时间差,称作“地方时”。
上述的情况可以归纳为:在一个惯性系中同一个地点发生的事件的过程测得的时间就是“原时”;在一个惯性系中不同的地点发生的一个事件的过程测得的时间就是“地方时”。同一事件的测得的“地方时”总会大于“原时”。请记住这个结论,对于讨论许多问题会带来方便。
我们还可以把这个问题反过来进行分析。
路基上人看到列车上的钟走慢了,那么,列车上的人是否看到路基上的钟(假设也有一只类似的爱因斯坦光钟)也走慢了呢?路基上的人看自己的光钟里的光束来回一次走的是30万公里,需要1秒,但是在列车上的人看来,路基光钟里的光束前端是从东向西走的也是两条斜边,走过的距离也大于30万公里,又因为光速是不变的,车上的观测者一定看到路基上的钟走慢了。
这就出现了一个有趣的问题:究竟是谁的钟走慢了呢?
正确的回答是这样的:无论是车上的观察者或者是车下的观察者说得都是正确的,他们看到对方的钟都走慢了。因为,他们是生活在两个不同的但对称时空中,运动是一个相对的概念,这里没有一个统一的时空,来比较那一只钟走得快,那一只钟走得慢。
在这里的讨论可以看到,并没有一个绝对的、单一的、普适的、真实的时间,而只有从属于一个具体惯性系的时间。不同惯性系中,同一个事件的过程,有不同的计时值。在人类漫长的实践活动积累的经验中,都未发现过这样的情况,因此这是一个很难接受的观念,但由于光速不变,即在不同的惯性系中是同一个值,这是一个实验与理论都证实了的结论,你得去理解和接纳这样的事实。
这里普遍的法则是:相对于你运动的钟走得慢了,而相对于你静止的钟走得是最快的。
一位朋友在你面前走过,应当说他手上的表(与你的表结构一样)相比你手上的表走慢了。这种钟迟的效应就会发生,但这种效应在日常情况下是根本无法察觉出来的。如果你的那位朋友,能1秒钟从中国的最北端的漠河到最南端的曾母暗沙,飞越约5500公里,这个速度是够快的了,但也只有光速的1.8%,他的表显示这个效应(比你的表走得慢些)也只有万分之二秒,将近3小时能慢1秒多一点,这原本是一件几乎无法实现的事情,就更谈不上能察觉到这种时差。因此在通常的情况下,我们是不会察觉到运动的钟走慢了的现象
三、光速不变,运动的物体变短
用光速不变,还能导出一个物体的长度会沿着运动方向发生收缩。
长度的收缩是空间的变化,因此首先要说一下什么是空间。
什么是空间?简单地说,就是可以用尺子进行量度的那个“东西”。尺子就是测量那个“东西”的工具。空间是对一个具体的物体而言的。用尺子量得一个物体的长、宽、高的值,就有了属于这个物体的空间大小。
要测量一个高速运动物体的长度在运动方向发生的变化,很难实际操作。我们只能把这种测量设计成一种理想实验,当然这里的理想实验在理论上是能够成立的。下面设计的理想实验,就是测量一张运动的桌子长度,然后与它静止时的长度进行比较。
设有一张桌子在高速列车上,列车由西向东行驶,车上的观察者相对于桌子是静止的,他如何来测量这张桌子的长度呢?这很简单,与我们在室内量一个桌子的长度是一样的:把尺子对齐桌子的两端,看一下尺子上的读数就可以得到桌子的长度,假定测量的结果是L0。因为这是测量者与桌子相对静止的情况下测得的,可以把L0称作桌子的静长。
然而,这个测量结果与列车的运动无关,为了能与一张运动桌子测得的长度进行比较,必须找到一种测量方法,把测量桌子的长度与列车的运动联系起来。
为了建立这种联系,车上的观测者可以在路基上找到一个标记,利用这个标记来测量桌子的长度。
车上的观测者看到在路基上A处有一根柱子,把它作为一个测量的标记。列车上的测量者知道列车运行的速度是V,当桌子前端通过柱子时记下时间,又当桌子的末端通过柱子时记下时间,若时间的差为△t,那么,这张桌子的静长L0应当等于 V△t,即有L0 = V△t。
要注意的是:这个时间差△t,是在列车上的两个地方(桌子的前端和后端)测得的,因此是“地方时”。
假定车下有一位观测者,就站在A处的柱子前,来测量这张桌子的长度。他手里拿着一只与车上测量用的一样的钟,当桌子的前端通过他时,他记下了时间,又当桌子的末端通过他时,又记下了时间,这两个时间的差△t’记录了桌子通过他的时间,这样,他测得桌子的长度显然是运动桌子的长度,记作L,L=V△t’。
要注意的是:这是在路基上同一个地点记录的时间,因此是“原时”。
上面车上、车下的测量,都没有用尺子,用的是相同的钟,而匀速运动的列车速率V是一个不变的值。
从上面的讨论已知,“原时”总是比“地方时”小。它们之间的关系是
这个重要结果就是从光速不变得到的,下面就可以用这个结果来得到桌子的长度在运动方向上的发生的变化。
比较一下两个测量的长度,因为
因此就有
代入上式,即有
这一结果告诉我们:运动的桌子其长度缩短了一个β因子。
如果车速是0.8C,可算得β=0.6,代入公式计算,如果桌子静止时长度为120厘米,则运动起来的桌子长度只有72厘米,缩短到约只有原长的60%。
因为光速不变,我们又得到了狭义相对论的第二个重要结论:运动物体在其运动方向上的长度收缩了。
在高能物理领域里,钟迟、尺缩的相对论效应一次次被实验所证实。一种称作μ子的亚原子粒子,是一种不稳定的客体,你若观察到一个静止的μ子寿命只有2微秒,极快地衰变为电子和中微子。
宇宙射线在大气上层产生的μ子速度极大,可达0.998C,如果没有钟迟效应,从它产生到衰变这段时间里平均走过的距离约为600米,如果是这样,μ子是不可能到达地面实验室的,但实际上μ子可以穿过大气超过9000米,到达地面实验室被接收到。这是因为它的高速运动延长了寿命,地面上看到μ子的寿命将是
这样μ子在这段时间里通过的距离为9500米,与观测到的结果一致。
也可以用缩尺的效应来解释上述现象,当μ子以0.998C的速度垂直向下穿过大气层时,也可以认为μ子是静止的,大气层相对于μ子以这个速度运动,运动中大气层的厚度就缩短了,其缩短的厚度为:
这正是预料中的结果。
以上的分析可以看出,由于光速不变,时间与空间可以发生了转换:地球上的观察者,看到μ子寿命的延长,因此能穿过厚厚的大气层;μ子却“认为”,大气层相对于“我”在运动,它的厚度收缩了,“我”虽然寿命不长,但也能穿越厚厚的大气层。
一个参考系中可以认为运动钟走慢了;在另一个参考系中,可以认为距离变短了,都得到相同的结果。这就是说,在一个惯性系中看到时间的膨胀;在另一个惯性系中看到的是空间的收缩,空间与时间在不同的惯性系之间发生了替换。如此看来,由于光速不变,让我们看到空间和时间都不是独立存在的东西,它们是相互纠缠在一起的。
今天的大多数人们仍然是把空间和时间看作是绝对的东西。狭义相对论给出的结论是在我们的直觉之外,我们感觉不到它,由此也就带来理解上的困难。原因是简单的,因为理论依赖于运动的速度,而汽车、飞机甚至宇宙飞船的速度,产生的效应微不足道,站在地上的人与坐在汽车、飞机上的人确实在经历着不同的时间和空间,但因差别太小而无法感知到。有朝一日,人们真能坐上接近光速的宇宙飞船去旅行,相对论效应将会变得十分显著。到那时,人们就会很自然地接受和理解这种时空的性质。
四、光速不变,同时是相对的
光速不变,我们原先理解的“同时”概念,也发生了变化。
在这组文章的《之三》中。我们看到,通过发射垒球的实验,证明了在车上同时发生的两件事,在车下也是同时发生的。同时对于车上、车下没有什么区别,在不同的惯性系中都一样,是一个绝对意义上的概念。
在非相对论的情况下,我们做一个分析,来说明这种同时的绝对性。
在一个由西向东高速行驶的列车中部,一起向车厢两端水平发射两只垒球,车上的观察者看到这两只垒球同时到达车厢的前后壁上。这是很好理解的一件事,虽然列车是高速,但它是匀速运动的,是一个惯性系,这里看到的现象与在实验室里看到的是一样的。在地球上一个静止的实验室中央,向东西两个方向同时水平发射两只垒球,且速率一样,那一定是同时到达距离相等的实验室的前后壁上。
我们再在列车上做这一实验,并作一个计算。
设球速是u,车速是v。车厢全长是2L,则半个车厢长为L,垒球撞击前、后壁的时间记作△t0,显然△t0= L/u。
我们再来分析路基上的观测者看到的情形。
对于路基上的观测者,他看到的向东飞行的垒球的球速是(u+v),如果球撞到前壁的时间是△t,则球在撞到前壁过程中,飞行的距离是(L+v△t),撞击前壁的时间
△t = (L+v△t)/(u+v),
可解得
△t = L/u =△t0
与列车上的观测者测得的时间是一样的。
向西发射的垒球的速度是u与v相减。因此东行的球的速度要比西行球的速度要大,但是,车厢的后壁也在向东跑,西行的球虽然速度小,但是车厢的后壁是“迎着”球而来,这样用时就少。设球撞击后壁的时间为△t’,则
△t’= (L-v△t’)/(u-v),
可解得
△t’= L/u = △t0
因此车上、车下的观察者看到两球都是“同时”到达前、后壁的,在一个惯性系中同时发生的事情,在另一个惯性系中,也是同时发生的,这就是同时的绝对性。
对于光的运行情况就不一样了,因为光不是垒球,它无论在哪一个惯性系中(无论是列车上还是路基上)光速都一样,正是由于光速不变,同时性就发生了变化。
路基上的观察者,看到由列车的中间向两端发出的光脉冲,都是以速度C向车前、向车后运动,由于列车向东行驶,前端的光脉冲要去“追赶”向前运动的车厢前壁,而后端的光脉冲是“迎着”车厢的后壁,而这里前后光脉冲的光速又都是一样的,显然后壁的碰壁事件将先于前壁发生。列车上的观察者看到同时发生的事件,路基上的观察者看到的不是同时发生的,是车厢后端的事件先发生,而车厢前端的事件后发生。
由于运动的相对性,如果认为列车不动,路基由东向西运动,那么不难证明,路基上在不同地点同时发生的两事件,由于光速不变的原因,列车上的观察者一定是看到前面(靠东边)的事件先发生,后面(靠西边)的事件后发生。
由于这种同时的相对性,也可以用来解释运动的桌子缩短的原因。因为车上的人看到路基上的观测者对桌子的测量不是同时进行的,而是先东后西,车子是向东开,先量桌子的东端,再量桌子的西端,在这个时间间隔中,桌子东行了一段,当然把桌子量短了。
从这里可以看到,由于不同参考系中同时的相对性,运动物体的长度发生了收缩。这显然不是像洛伦兹所说的物体本身的收缩,是由于被测对象的运动,时空发生了变化引起了同时的相对性而出现的测量的效应。
如果宇宙间的信号可以用无限大的速度传递,那么就可以绝对地确定两个事件是不是同时发生的,同时就有绝对的意义。由于光速不变,而且是一个有限的速度,这样宇宙间传递信号的最快速度也是有限的,对于不同的观测者,“同时”这个概念就只能有相对意义。
可以用一个例子来帮助你理解这件事。
因为声速有限,可以用声音的传播做一个比较。设A、B两个声源发出的声音,如果甲在A、B连线的中间同时听到了这两个声音,甲认为这两个声音是“同时”发出的;如果乙在A、B连线的延长线上,靠近B端,那他一定会觉得B先发声,而A后发声。乙就认为不是同时的了。
如果这里的声速是无限大,甲、乙就一定都会认为A、B是同时发声的。由此可以看出,如果传递信号的速度无限大,那“同时”就具有绝对性,如果没有无限大的信号传递速度,那“同时”只能具有相对意义。
经典力学认为同时是绝对的,就是虚设了这样一种情形,宇宙间传递一个信号不要用一点时间,这是一种人为假定的理想状态,并不真实存在,而相对论被大量实验所证实,是一个符合实际的可被实验验证的理论。
千百年来,人们一直以为同时的概念是绝对的、普适的,而光速有限否定了这一结论。
实验已经否定同时的绝对性,这就说明宇宙间不存在无限大的速度,既然没有了无限大的速度,就一定会存在一个最大的速度,这就是宇宙间的极限速度。
什么是宇宙间的极限速度?我们来做一个逻辑的分析。
如果在同一个惯性系中,测量万物的速度,光速是一个最大的值;如果在速度不同的各种惯性系中,来测量万物的速度,光速也是最大值。这就得到了三个重要结论:光速就是宇宙间的极限速度;光速在各个惯性系中都应当是精确相等的;光束的运动不同于任何其他物体,它应当是宇宙间万物的另类。
既然宇宙间的极限速度就是光速,它具有不随参考系变化的属性,而物理定律都具有这样的属性,这样“光速不变”显然可以处于物理学中的一个基本定律的等同地位。
如果“同时”是相对的,有的读者可能会产生这样的疑问:事情的先后次序是不是也可以是相对的?那么,是不是会出现在某个参考系中能看到一个人的死亡早于他的诞生,一列火车的到站早于它的出发呢?
这是不可能的,我们仍然用列车中部向两个方向发出光信号来作说明。
在向东飞驰的列车上,观察者看到光信号同时到达车厢的前后壁,而路基上的观察者,看到光信号先到达后壁,后到达前壁。但是由于光速是一个有限的速度,它从列车的中间传向前后两壁总是需要时间的,无论如何也不会发生在脉冲还没有发出之前,就发生了后壁的撞击事件,这样的因果倒置显然是不可能的。
狭义相对论告诉我们,光速C是一个不变速度,而且是一个极限速度,这就保证了我们在任何惯性参考系中不会看到“倒因为果”的荒诞现象,有因果联系的两事件的顺序是绝对不变的。
千百年以来,人们一直以为同时的概念是普适的,与运动状态无关的,光速不变则要求我们放弃这个观点。
五、光速不变,质量可变
光速不变,还改变了人们对于物体质量的看法。
我们知道牛顿理论的核心是第二定律F = ma。这一方程告诉我们对一个物体(m)施加一个力(F),物的运动状态会发生改变(a)。如果对物施加一个不变的力,则物体将会保持一个不变的加速度,即速度可以不断地增加,这样物体的速度不但可以达到光速,而且还可以出现超光速现象,这显然与狭义相对论相悖。
让我们回忆一下几个中学生在E城的活动。在路基上的一位学生,当一列接近光速的列车飞驰而来,到她面前时,她推动列车上的一个1千克的物体,按牛顿理论,它仍然可以获得1米/秒2的加速度,但光速是一个不变的极限速度,这个物体在接近光速的情况下,再要加速,就很困难了,出现这种困难的唯一解释只能是这个物体的惯性变大了,即它的惯性质量增大了。
在上述的实验中,根据计算,当1千克的物体以0.8C运动时,质量会变成1.6千克;当以0.9C运动时质量会变成2.1千克;接近光速运动时,质量会变得很大、很大,此时,她们事实上根本不能推动原本是1千克的物体。
这就是说,由于光速不变,而且是一切物体运动的极限速度,那么就必然会得到这样的结论:在高速运动下的物体会有更大的质量,或者说,一个物体的质量随其速度的增大而增大,当速度接近光速时,它的质量可以趋于无限大,这就确保任何一物的运动不能超过光速。正如爱因斯坦所说:“超光速的速度——像我们以前的结果一样——没有存在的可能。”
质量随速度变大的理论被许多实验事实精确地证明。在20世纪70年代所做的实验中,当电子被加速,它的速度与光速的差不超过100亿分之三时,电子的质量已是静止质量的4万倍了。
六、质量可变,能量亦变
上面的讨论告诉我们,由于光速不变,会导致物体运动时的质量随之增大。物体运动是动能增大了,这就是说,物体动能的增大时,其质量也会增加。从这个例子中我们似乎看到,能量中也有质量,能量与质量存在着某种联系,或者从根本上看,它们就是一回事。
从相对论和能量守恒定律出发,爱因斯坦发现,无论给予某个物体什么形式的能量,能量的增大都会导致质量的增加。推动此物动能增大了;举高此物,引力势能增大了;拉、压此物,弹性势能增大了;加热此物,内能增大了;给此物带电,电磁能增大了;凡此种种,只要此物的能量增大,其质量也要随之增加。
它们之间有一个定量联系的关系式,用文字表述是:给予一个物体能量的大小除以光速的平方,就等于这个物体的质量的增加,用符号表示是:
举两个简单的例子,说明这个公式的意义。
1千克的一个物体,加速到100米/秒(相当于每小时行驶360公里的高速列车)时,代入上式计算,因其动能的增大,也相当于增加了5.6×10^-14千克的质量,即增加了千亿分之一克质量,这是一个很小很小的量。动能变大了,质量也增加了,这说明能量中有质量。再比如燃烧一块煤,如果我们精确地称量煤块、灰烬、烟雾和反应过程中的其他物质,就会发现,会有很小很小一部分煤块的质量成为了辐射形式的能量。
事实上,这一结论告诉人们,一切质量有能量,一切能量也有质量。公式表示了质量与能量不同形式之间等当关系。质量与能量相当,它们组成了一个单一的不变量,人们称之为质-能。因为质量中有能量,能量中也有质量,因此它们之间没有转换,只有质量或能量的永远守恒,即质-能的守恒。
上述质量与能量的关系式是根据爱因斯坦著名的质能方程得到的。
爱因斯坦在发表完《论动体电动力学》之后3个月,即1905年的9月,发表了《物体的惯性同它所含能量有关吗?》在这篇文章中,专门讨论了这个问题。文中说:“如果一个物体以辐射的形式放出能量E,则它的质量减少E/c^2。这个事实与从物体抽出能量变为辐射能量显然没有什么区别,因此,这使我们得出更普遍的结论,物体的质量,就是它所含能量的量度。……”这就是说,质量可以用能量来量度,能量亦可以用质量来量度;所有形式的能量都具有质量,所有质量都等效于一定数量的能量,它们之间是等当的。
1907年,爱因斯坦提出了一个被后人称为“改变世界的方程”——质能方程:
E = mc^2
这一方程的发现是相对论理论的重要成就之一,是物理学中一个著名的方程,它曾被许多实际的应用和理论的结果所证实,是人类发现的自然界中隐藏很深的一个秘密。爱因斯坦认为这个方程是狭义相对论最有意义的一个结果,他宣称,物体的能量与质量不是两个独立的概念:我们可以从质量来决定能量,也可以从能量获得质量。
又当物体静止时,它的能量E也不等于零,而是等于E静= m0c^2,这个能量称为静能。在牛顿力学中是没有这个概念的,当然就没有静能形式的能量。由于c^2这个因子很大,小质量就能产生大能量(可参阅《麦克斯韦妖随笔之七》)。
曾给日本广岛带来毁灭性破坏的能量,只是不足8.71克的铀转化的能量;若能利用1千克物质的静能,可以使100瓦的灯泡点亮3000万年之久。人类只要能开发这种潜在于物体中的静能,能量的源泉可以说是用之不尽的。
今天,人类使用的原子能和核能,就是开发静能的一个途径。
这一方程的提出,还解决了一个长期悬而未决的问题。
直至19世纪,物理学家一直为恒星为何能长期燃烧而困惑。此方程出现后,人们都明白了,恒星之火是以它巨大的质量为燃料的,燃烧发出的巨大的辐射能就是作为燃料的质量一种存在形式。
离我们最近的恒星就是太阳,据观测太阳1秒内约燃烧5×10^9千克的质量,那么一年就是1.6×10^17千克,太阳的质量约为2×10^30千克,太阳以这样的速度燃烧,就可以估算出太阳的寿命为10^13年。现在太阳的年龄约为5×10^9年,所以说现在的太阳正处在中年。
E = mc^2这个方程,虽然形式简单,但它在物质世界具有最大范围的普遍性,显示了宇宙的大美,蕴含着自然界根本的秘密。它也许是人类在宇宙间能长久获得能量的希望。
大自然竟然会有这样的精巧的结构确实让人叹为观止;
爱因斯坦居然看到了这样的秘密着实让人惊叹不已!
作为经典力学的最基本的元素是位置、位移、速度、加速度、质量和力,后续的动量、能量等概念都可以看作是这些最基本的元素衍生出来的概念。前四个概念与空间、时间相关,质量的变化也改变了人们对于力和能量的看法。因此,光速不变,使得人们对时间、空间、质量、能量的看法均发生了变化。
光速不变,使得麦克斯韦方程在不同惯性系中形式保持不变,这也以一种新的观点加深了我们对电磁理论的理解。在电磁学中,电场和磁场各自独立的,是从电场之外假设一个磁场,而在相对论中,是以一种最自然的方式引入了磁场,是一个运动电荷对一个试探电荷施加了力的结果,磁场根本上就是电荷、速度与力构成的一个概念,不是另外需要假设的新东西。
光速不变,成了爱因斯坦建立他的理论最重要根基;
光速不变,带给原子物理、核物理、高能物理及固体物理根本性的变化;
光速不变,带来的是人们时空观念上的大变,带来的是物理世界从根底上的大变。