论文地址:PACDNN:一种用于语音增强的相位感知复合深度神经网络
引用格式:Hasannezhad M,Yu H,Zhu W P,et al. PACDNN: A phase-aware composite deep neural network for speech enhancement[J]. Speech Communication,2022,136:1-13.
摘要
目前,利用深度神经网络(DNN)进行语音增强的大多数方法都面临着一些限制:它们没有利用相位谱中的信息,同时它们的高计算复杂度和对内存的要求使得它们不适合实时应用。本文提出了一种新的相位感知复合深度神经网络(PACDNN)来解决这些问题。具体而言,该网络利用频谱掩模进行幅度处理和利用相位derivative(导数)进行相位重构,从而实现幅度和相位同时增强。此外,DNN经过精心设计,充分利用了语音对时间和频谱的强烈依赖性,而其各组成部分独立并行执行,以加快计算速度。通过大量的对比实验,证明了所提出的PACDNN模型相对于一些知名的基于DNN的SE方法的优势。
关键词:语音增强,深度神经网络,模型复杂度,频谱掩模,相位derivative
1 引言
在真实世界环境中获取的语音信号往往会受到背景噪声的干扰。这种干扰现象出现在语音识别、听力修复、语音通信、智能家居设备等许多应用中。语音增强(SE)的目的是抑制所采集的语音信号中不需要的环境噪声,以提高其质量或作为预处理程序,提高应用程序对各种噪声的鲁棒。SE方法可以是无监督的,也可以是有监督的。传统的Wiener滤波(Abd ElFattah等人2008年;Wang和Chen,2018)和基于统计模型的方法(Martin 2002;Parchami等人2016)是两类著名的无监督方法,它们依赖于语音和噪声的统计特性,当这些特性已知或适当建模时,会产生良好的性能。然而,在统计特性未知或难以建模的真实场景中,特别是在非平稳噪声条件下,这些方法的性能会下降。
近年来,随着快速计算硬件的发展和大数据集的可用性,监督方法在许多领域受到了越来越多的关注。特别是,基于深度学习的方法在语音处理方面取得了革命性的进展,包括语音识别。DNN在模拟高度复杂的转换方面的卓越能力极大地提高了在不利和可变的声学情景中的SE。此外,训练有素的DNN可以提供低延迟处理,这对许多实时应用非常重要,如助听器(Agnew和Thornton,2000)。在过去的十年中,已经提出了各种基于DNN的SE方法,下面将进一步详细介绍。
Xu等人(2014)利用多层感知器(MLP)将带噪语音的对数功率谱映射到纯净语音。在本工作中,一些关键的MLP问题,如过拟合和全局方差归一化问题,也进行了研究。虽然MLP模型获得了很好的SE结果,但由于其参数较多,复杂性较高。此外,MLP独立处理语音样本,即不考虑顺序信息,但语音却表现出很强的时间依赖性。Chen和Wang(2017)采用了长短期记忆(Long-Short Term Memory,LSTM)网络,一种递归神经网络(RNN)的变体,对语音的信息按时间顺序进行建模,结果表明LSTM能够在困难的嘈杂条件下跟踪这种说话人依赖的信息。他们还证明了LSTM网络在将模型推广到多个说话人和噪声方面优于MLP。最近,一个同时运行时间和频率的LSTM网络被用于提取低比特率音频恢复的时频模式(Abbaszadeh,2016)。虽然LSTM具有很好的SE性能,但它被认为是一个高度复杂的模型。为了缓解LSTM的这一问题,SE最近采用了LSTM的两种变体,即门控循环单位(GRU) (Dey和Salemt,2017)和简单循环单位(SRU) (Cui等人,2020)。然而,GRU和SRU虽然提供了LSTM的高效实现,但在SE应用中,它们的性能不如LSTM。
Park和Lee(2016)研究了SE的卷积神经网络(CNN),并将其所需参数数与MLP和LSTM进行了比较。特别是,他们表明,这三种方法几乎提供相同的SE性能,尽管CNN需要更少的参数。然而,本研究只考虑了参数的数量,而实际的复杂性和实现成本也取决于内存占用,CNN的内存占用会明显大于LSTM和MLP。我们还注意到,CNN最初的设想是为了从图像中捕获局部信息,而语音频谱通常表现出非局部相关性。此外,CNN网络的最大池化层只保留其输入的粗信息。因此,Oord等人(2016)引入了一个生成模型,该模型没有最大池化层,而是包含了一个扩张因果卷积层堆栈。该模型在不增加模型复杂性的情况下扩展了CNN滤波器的感受野。受此工作的启发,Ouyang等人(2019)在频域引入了一个全卷积模型,显示了有前景的SE结果。
与上述的独立学习方法相比,最近的一些研究考虑将网络组合作为SE的学习引擎。Tan和Wang(2018)引入了卷积循环神经网络(CRN)作为SE的编码器解码器网络。他们还通过引入门控卷积循环网络扩展了CRN Tan和Wang(2019),并获得了更好的SE结果。Zhao等人(2018)、Hsieh等人(2020)分别提出了其他一些基于频域和时域的CRN网络。Hu等人(2020)引入了一种深度复数CRN,其中CNN和RNN被设计用来模拟复数值target。该模型的优点在客观和主观指标方面都得到了体现。虽然CRN模型产生了很好的SE结果,但Strake等(2020)认为,由于不同CRN组件之间的数据被重塑,CNN feature maps的内部关系和局部结构被彻底破坏。因此,他们对SE采用卷积LSTM,将LSTM中的全连接映射替换为卷积映射。基于这一论点,最近Shifas等人(2020)在SE中使用了另一个名为gruCNN的模型块,在特征提取CNN层中加入了递归。这些组合网络取得了良好的SE效果;然而,它们都表现出非常高的复杂性模型,其中一些(由于它们的非因果形式)引入了额外的延迟。此外,当训练和测试数据集相同但分解为不可见数据集时,基于CRN的方法表现良好(Pandey和Wang,2020)。
虽然上述方法在语音增强中取得了显著的效果,但大多数方法只对语音的幅度增强进行了研究,而没有对相位进行处理。这是因为相位谱的高度非结构化,使得DNN对其进行估计非常困难。然而,Krawczyk和Gerkmann(2014)指出了相位增强在语音增强环境中的作用和重要性,从而提出了不同的相位感知方法。Erdogan et al. (2015) 提出了将相位信息纳入DNN处理的最早尝试之一,其中引入了相位敏感掩模(PSM)。然而,该方法主要利用PSM对语音的幅度进行处理,并在语音重构中使用噪声相位。Williamson等人(2015)引入了一种复数理想比率掩模(cIRM),将掩模分为实部和虚部来增强复数谱。不幸的是,使用cIRM会在增强语音中引入失真,因为其虚部中缺乏可识别的模式(Yin等人,2020 Hasannezhad等人,2020a)。Fu等人(2017a)、Tan和Wang(2018)、Ouyang等人(2019)、Tan和Wang(2019)也提出了直接估计复数谱的方法,使用DNN从嘈杂语音中估计纯净语音复数谱的实部和虚部。然而,这些方法需要大量的数据集来学习精确的映射函数;此外,他们在未见数据上的表现可能比简单的频谱映射方法更差(Pandey和Wang,2020)。Yin等人(2020)引入了一种相位和谐波感知(harmonics aware)的降噪模型,其中提出了一种两流DNN结构,在幅值和相位谱之间进行信息交换,以恢复纯净语音的复数谱。由于相位谱本身具有不规则的结构,研究人员还研究了从相位导出的其他量,这些量显示出与语音重构的幅度相似的结构(Mowlaee和Saeidi,2014)。Takamichi等(2018)尝试基于DNN估计重建相位。作者引入了一种von-Mises分布的DNN进行相位重构,该DNN具有预测和实际分组延迟(group delay,GD)之间的损失函数。在他们随后的工作中(Takamichi et al.,2020),他们在相同的框架中使用了一个方向统计DNN,并引入了正弦偏广义心线分布DNN来建模GD。Zheng和Zhang(2018)提出了一种相位感知模型,联合处理幅度和相位谱,其中通过频谱掩模获得估计的幅度,通过相位导数(PD),即所谓的瞬时频率偏差(IFD)重建相位。实验结果表明,该相位感知模型比基于cIRM和仅幅度掩模的方法具有更好的性能。然而,它使用MLP和LSTM来估计目标,这限制了可达到的精度,并招致较高的计算成本。此外,虽然IFD在相位重构中得到了有效的应用,但GD等其他PD可能具有更好的性能。
在一项初步研究中(Hasannezhad et al.,2021),我们提出了一种融合CNN和LSTM的SE复合模型。具体而言,该模型采用改进的LSTM和CNN结构,利用包含语音频谱和时态上下文信息的互补特征集,从而优于一些已知的基于DNN的SE方法。在本文中,我们通过引入新的思想和处理模块来进一步研究该模型的相位和幅度增强。受Zheng和Zhang(2018)的启发,我们提出了一个名为相位感知复合深度神经网络(PACDNN)的新模型,该模型涉及两个子任务:频谱掩模的幅度处理和PD的相位重建,其中DNN同时估计两个目标。我们研究了不同类型的掩膜和PD,以及它们可能的组合,以选择DNN的最佳目标。我们的分析和实验研究表明,与现有的几种基于DNN的方法相比,本文提出的PACDNN模型具有更好的SE性能,同时显著降低了计算复杂度和内存占用。
本文的其余部分组织如下:第2节描述了提出的PACDNN模型及其组成部分。然后,第三节给出了实验,并对实验结果进行了比较和讨论。最后,本文在第4节进行总结。
2 提出PACDNN模型
本文提出的PACDNN模型的框图如图1所示。该复合模型将CNN和LSTM流相结合,提取一组互补的特征,然后转化为网络target。复合模型输入由Noisy组成,输出由频谱掩模和PD组成。在测试阶段,利用估计的掩模和PD 重构纯净语音。以下将讨论PACDNN模型的各个组成部分。
图1 高级PACDNN模型
2.1 复合模型
2.1.1 改善LSTM stream
语音频谱表现出很强的时间相关性,这对SE很有用。LSTM可以对这些长期依赖关系进行建模,因为它将输入帧视为一个序列。具体来说,它可以模拟语音随时间的变化,并学习语音的时间动态(Wang和Chen,2018)。LSTM由一个存储单元和三个控制门组成:遗忘门、输入门和输出门。$M$和$N$分别表示输入向量和cell状态的大小,LSTM可训练参数的数量是$4*(N^2+NM+N)$(Dey和Salemt,2017)。
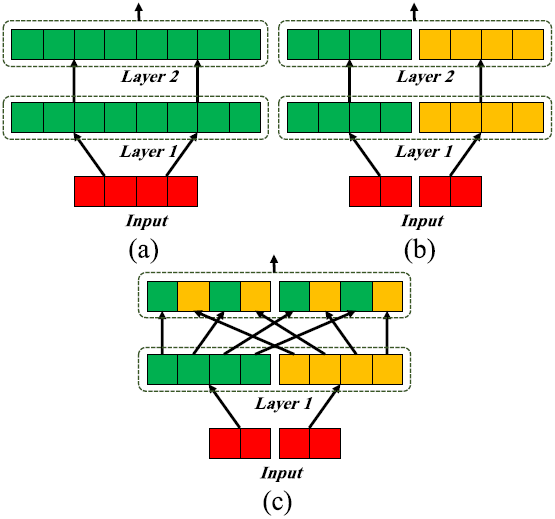
LSTM网络的一个关键问题是它的高复杂性,这源于权值和递归矩阵中的参数冗余。前者转换特征表示,后者在连续步骤之间转换隐藏状态。为了规避这些冗余,Gao等人(2018)引入了一种分组循环网络。考虑双层LSTM网络,如图2(a)所示。如所知,忽略偏置项的单门LSTM的参数为$(N²+N*M)$。通过将输入层和隐藏层拆分为独立执行的$K$组,参数的数量减少了一个因子$K$,如下所示
$$公式1:K \cdot\left(\left(\frac{N}{K}\right)^{2}+\frac{N}{K} \cdot \frac{M}{K}\right)=\frac{N^{2}+N \cdot M}{K}$$
这样的分组网络图2(b)所示其中K= 2。分组策略虽然降低了模型的复杂度,但降低了网络的效率。事实上,虽然捕获了组内的时间依赖关系,但由于不同的组不能通信,组间的依赖关系会丢失。为了解决这个问题,Gao等人(2018)提出了另一种重新安排,将不同的群体连接起来。该技术可以在不引入额外参数的情况下使用基本张量运算来实现,如图2(c)所示。因此,我们使用这种分组和连接重排来降低模型的复杂性,同时保持性能几乎相同。
图2所示 2层分组LSTM:(a)未分组;(b) K =2分组;(c)分组和表示法重排
2.1.2 改善CNN stream
扩张频率卷积:CNN最初是为图像分类而设计的。传统的CNN由成对的卷积层和池化层以及一个完全连接的网络组成。前者的目的是提取特征,后者的目的是完成分类。
将语音频谱看作是一幅图像,CNN可以利用其频谱上下文信息。然而,由于CNN核的感受野有限(来自前一层的局部区域),CNN只能捕获输入的局部信息,而语音频谱沿着频率轴显示非局部相关性。在图像处理应用中,引入了扩张卷积来增大CNN核的感受野(Yu and Koltun,2015)。根据我们最近的研究(Hasannezhad等人,2021年),我们使用了一个具有堆叠的扩张卷积来捕获非局部频谱相关性,而不增加模型复杂性。此外,采用残差学习和跳跃连接技术,以促进训练和加速收敛。值得注意的是,这个全卷积CNN结构没有池化层。
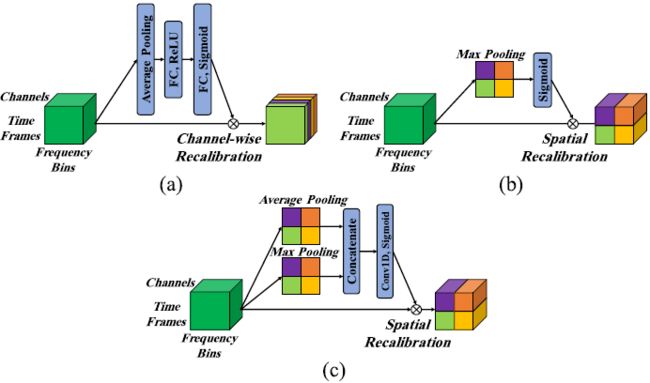
注意力驱动的CNN: CNN包含许多特征图,这些特征图可能具有不同的显著性水平。因此,强调信息特征映射可以提高模型的性能。通过重新校准特征映射,注意机制自适应地强调信息映射,同时抑制其他信息映射。Hu等人(2018)提出了一种成功的注意力机制,称为挤压与激励(squeeze-and-excitation,SAE),专注于通道关系。在这种方法中,如图3(a)所示,在squeeze阶段,平均池化操作将每个特征映射的全局信息在空间上聚合到一个通道描述符。然后,一个全连接的网络通过调整激励阶段的描述符来捕获通道方面的依赖关系。最后,通过excitation值对原始特征图进行重新校准,并将结果传递给后续层。受SAE的启发,但旨在利用像素级空间信息,Roy等人(2018)引入了空间SAE,如图3(b)所示,其中挤压操作沿通道进行,而激励为空间激励。Woo等(2018)引入了卷积块注意模块,如图3(c)所示,该模块结合了通道方向和空间方向的SAE。在这种方法中,平均池和最大池都被用作挤压器。然后将压缩模块的输出连接起来,并通过一个S型激活函数传递。最后,将得到的权值以元素方式应用于原始的特征映射。在本文中,我们研究了这些注意力机制在PACDNN模型中的使用。
图3所示 注意力机制:(a)采用平均池的通道方式;(b)具有max-pooling的空间;(c)具有Max和average-pooling的空间
2.1.3 回归(Regression)
如图1所示,所提出的PACDNN复合模型中的两个并行流利用互补的特征集,然后转换成频谱掩模和PD值。这种转换可以通过一个低复杂度的CNN或一个MLP网络来实现。这两种DNN类型具有不同的属性,尽管它们都可以完成所需的回归任务。如Fu et al. (2017b)所述,CNN可以模拟相邻元素之间的快速波动,而MLP不能。此外,CNN需要的模型参数比MLP少得多,而后者需要的计算内存更少。我们将从不同的角度比较这两个网络的回归任务,包括SE性能和计算复杂度。
2.2 频谱掩模和相位导数计算
如上所述,PACDNN中复合模型的目标由频谱掩模和PD两部分组成。前者用于噪声幅度谱的增强,后者用于相位谱的重建。选择合适的target对最终的增强性能至关重要。
考虑带噪语音$y(t)$为纯净语音$s(t)$与噪声$n(t)$的相加,其中$t$为离散时间指标,利用短时傅里叶变换(STFT)将时域带噪语音转换为TF域,即
$$公式2:Y(k,l)=S(k,l)+N(k,l)$$
式中,$Y(k,l)$、$S(k,l)$和$N(k,l)$分别表示带噪语音、纯净语音和噪音的STFT谱,$k$和$l$分别表示帧索引和频率bin索引。复数谱可以用极坐标表示,即幅度谱和相位谱。例如,纯净语音的声谱可以分解如下
$$公式3:S(k,l)=|S(k,l)| e^{i \phi_{S}(k,l)}$$
其中$\phi$和$|·|$分别表示相位和幅度。在本文中,我们的目标是通过联合重建幅度谱和相位谱,以获得增强的语音。下面介绍几种流行的掩膜和PD。在我们的研究中,通过考虑这些掩膜和PD的不同可能组合来评估增强性能。
2.2.1 频谱掩码
受人类听觉系统掩蔽效应的启发(Wang and Chen,2018),掩蔽算法的目标是在TF域中保留带噪语音中的纯净语音,同时抑制噪声。为此,文献中介绍了不同的mask,本研究总结如下
理想比率掩模(IRM) (Srinivasan et al.,2006)定义为在噪声与纯净语音不相关的前提下,在TF单元内纯净语音与带噪语音的能量之比。
$$公式4:\operatorname{IRM}(k,l)=\left(\frac{|S(k,l)|^{2}}{|S(k,l)|^{2}+|N(k,l)|^{2}}\right)^{\frac{1}{2}}$$
频谱幅值掩模(Spectral amplitude Mask,SMM,也称为IAM) (Wang et al.,2014)定义为纯净语音的频谱幅值与带噪语音的频谱幅值的比值,其概念与IRM相似,即
$$公式5:\operatorname{SMM}(k,l)=\frac{|S(k,l)|}{|Y(k,l)|}$$
最优比率掩码(ORM) (Liang et al.,2013)是基于最小化纯净语音和估计语音之间的均方误差(MSE)而得到的。它由
$$公式6:\operatorname{ORM}(k,l)=\frac{|S(k,l)|^{2}+\Re\left(S(k,l) N^{*}(k,l)\right)}{|S(k,l)|^{2}+\left|N(k,l)^{2}\right|+2 \Re\left(S(k,l) N^{*}(k,l)\right)}$$
其中$*$和$R$分别表示共轭运算和实部。ORM和IRM的主要区别是前者中出现了$\Re(S(k,l)N*(k,l))$。因此,ORM可以看作是IRM的改进版本,它考虑了纯净语音与噪声之间的相关性。
相位敏感掩模(PSM) (Erdogan et al.,2015)定义为纯净语音频谱与带噪语音频谱比值的实部,如
$$公式7:\operatorname{PSM}(k,l)=\Re\left(\frac{S(k,l)}{Y(k,l)}\right)$$
由于我们在PACDNN中使用sigmoid作为输出层的激活函数,因此训练输出值必须限制在[0,1]。虽然IRM的值在期望的范围内,但ORM、PSM和SMM的值并不局限于此范围。因此,这三个掩码异常值被截断为[0,1]。
2.2.2 phase derivative
在一些相位感知语音增强方法中,采用局部相位处理代替相位本身。在这方面,瞬时频率(IF,instantaneous frequency) (Stark and Paliwal,2008)和群延迟(GD,group delay) (Hegde et al.,2007)是最著名的两个PD。
瞬时频率(IF)定义为相位谱的一阶时间导数。对于频谱,IF可以用连续两帧之间的相位差近似为
$$公式8:\operatorname{IF}(k,l)=\operatorname{princ}\{\phi(k+1,l)-\phi(k,l)\}$$
其中函数princ{·}表示主值算子,将相位差投影到$[\pi,\pi)$上。由于IF受其主值的限制,绕包效应将沿频率轴发生。为了缓解这个问题,Stark和Paliwal(2008)采用了如下的瞬时频率偏差(IFD)
$$公式9:\operatorname{IFD}(k,l)=\operatorname{IF}(k,l)-\frac{2 \pi}{N} k L$$
其中$\frac{2\pi}{N}kL$为$IFD(k,l)$的中心频率。
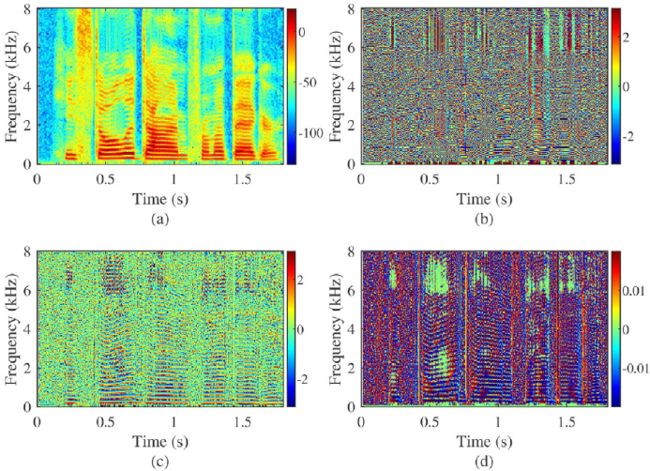
Stark和Paliwal(2008)证明,中频值跟踪基音谐波峰值的频率,而IFD值捕获基音和共振峰结构,如量级谱中所示。Zheng和Zhang(2018)也有类似的发现,他们从估计的IFD中重建了相位,用于语音增强。他们还表明,可以用DNN估计IFD,因为它显示出与频谱相似的模式,如图4 (a,c)所示。
分组延迟(Group delay,GD)是频谱相位相对于频率的导数的负值,由
$$公式10:\mathrm{GD}(k,l)=-[\phi(k,l+1)-\phi(k,l)]$$
在Hegde等人(2007)的文章中,作者证明了 GD 函数在共振频率下表现得像平方幅度响应。 它还表现出类似于幅度谱的结构模式,如图4(a,d)所示。 此外,Prasad 等人 (2004) 讨论的高分辨率特性,揭示了 GD 比幅度谱具有更高的分辨能力。 具体而言,与幅度或线性预测谱相比,在GD谱中共振峰的解析更准确。 基于这一发现,我们推断 GD 也可以用作基于 DNN 的 SE 的训练目标,与广泛采用的幅度目标或其变体相同。
图4所示 在采样频率为8 kHz时的语音频谱图:(a)幅度(对数刻度);(b)相位;(c) IFD;(d) GD
由于mask和PD是用一个DNN联合估计的,因此它们的值应该在相同的范围内,以平衡训练过程。我们采用Zheng和Zhang(2018)的归一化方案,将频谱掩模的范围截断为[0,1],将PD值归一化如下
$$公式11:\mathrm{PD}_{\mathrm{n}}(k,l)=\frac{1}{2 \pi} \mathrm{PD}(k,l)+\frac{1}{2}$$
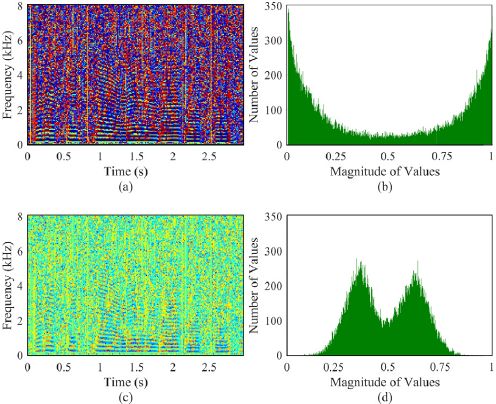
从图5 (a,b)可以看出,归一化GD值在范围内呈U形分布[0,1],这使得使用DNN对其进行精确估计更加困难(Zheng and Zhang,2018)。因此,我们建议使用以下转换来正则化归一化GD,即
$$公式12:\operatorname{RGD}(k,l)=\mu+\sqrt{2} \sigma \cdot \operatorname{erf}^{-1}\left(2 \mathrm{GD}_{n}(k,l)-1\right)$$
其中$erf^{-1}(·)$为逆误差函数,$\sigma$和$\mu$分别设为0.1和0.5。RGD及其分布如图5 (c,d)所示,将其值拉到中心点(0.5)附近,使RGD成为更好的训练目标。
图 5 采样频率为 16 KHz 的群延迟正则化干净语音:(a) GD 频谱图; (b) GD 值的分布; (c) RGD 频谱图; (d) RGD 值的分布。
2.3 幅度和相位重建
在这个小节中,我们解释如何从频谱掩模和PD估计中恢复幅值和相位谱。
2.3.1 幅度重建
从训练好的DNN中得到估计的频谱掩码$\hat{M}(k,l)$后,通过将频谱掩码应用于带噪语音的幅度谱来完成幅度重建,即
$$公式13:|\hat{S}(k,l)|=\hat{M}(k,l)|Y(k,l)|$$
通常,如果一个TF单元是语音主导的,$\hat{M}(k,l)$将有一个很大的值,这有助于在该单元中保存语音信息。否则,$\hat{M}(k,l)$将很小,从而有助于抑制背景噪声。如2.2.1节所述,本文研究了四种掩码$M(k,l)$,即IRM、SMM、ORM和SMM。
2.3.2 相位重建
在通过训练有素的 DNN 获得估计的 PD 后执行相位重建。 由于 IF 和 GD 分别定义为频谱图的 TF 单元之间沿时间轴和频率轴的相位差,因此需要对某些选定的 TF 单元进行适当的初始相位估计来恢复相位频谱图。 基于初始估计,可以通过(8)和(10)中的差分方程沿时间和频率轴重构整个相位谱图。
(1) 初始相位估计:当纯净语音功率远大于噪声功率时,噪声相位近似等于纯净相位。因此,在具有较高信噪比(SNR)的TF单元中,使用噪声相位作为初始估计是合理的。正如Zheng和Zhang(2018)提出的,我们采用噪声相位谱作为纯净相位的初始估计,即:
$$公式14:\hat{\phi}_{i n i t}(k,l)=\phi_{Y}(k,l),\forall k,l$$
然后我们使用每个TF单元的局部信噪比作为一个指标来确定初始估计的可靠性,其中局部信噪比近似于估计的掩码$\hat{M}(k,l)$。
(2) 利用GD进行相位重构:首先将估计的RGD(记为$\hat{RGD}(k,l)$)通过下面的变换映射回$GD_n(k,l)$
$$公式15:\widehat{\mathrm{GD}}_{n}(k,l)=\frac{1}{2}\left(\operatorname{erf}\left(\frac{\widehat{\operatorname{RGD}}(k,l)-\mu}{\sqrt{2} \sigma}\right)+1\right)$$
其中$erf(·)$为误差函数。然后通过对$\hat{GD}_n$进行去规格化得到估计的GD
$$公式16:\widehat{\mathrm{GD}}(k,l)=2 \pi\left(\widehat{\mathrm{GD}}_{n}(k,l)-\frac{1}{2}\right)$$
受Zheng和Zhang(2018)用IFD进行相位重构的启发,我们使用初始相位估计和初始估计与目标相位之间的GD计算相位谱。对于每个TF单元,我们生成$2N_s+1$帧条件相位估计,由
$$公式17:\hat{\phi}^{i}(k,l)= \begin{cases}\hat{\phi}_{i n i t}(k,l+i)+\sum_{n=0}^{i-1} \widehat{\mathrm{GD}}(k,l+n),& i \neq 0 \\ \hat{\phi}_{i n i t}(k,l+i),& i=0\end{cases}$$
其中$-N_s\leq i\leq N_s$是初始化的TF单元与目标TF单元之间的帧距离。在这项工作中,我们的$N_S = 2$。然后将这些阶段估计展开,即
$$公式18:\bar{\phi}^{i}(k,l)=\operatorname{unwrap}\left(\hat{\phi}^{i}(k,l) \mid \hat{\phi}^{i}(k,l-1)\right)$$
$(k,l)^{th}$单元的重构相位最终通过以下加权平均操作平滑帧条件估计$\bar{\phi ^i}(k,l)$得到
$$公式19:\hat{\phi}(k,l)=\frac{\sum_{i=-N_{s}}^{N_{s}}(s(i) \hat{M}(k,l+i)) \bar{\phi}_{i}(k,l)}{\sum_{i=-N_{s}}^{N_{s}} s(i) \hat{M}(k,l+i)}$$
其中$s(i)$表示$\bar{\phi^i}(k,l)$的邻近权重,它与帧距离的绝对值成反比,即距离|i|较大的相位估计$\bar{\phi^i}(k,l)$被分配一个较小的邻近权重$s(i)$,并减少其对$\hat{\phi}(k,l)$的影响。 在这项工作中,继 (Zheng and Zhang,2018) 之后,我们选择$s(i)$作为汉明窗。 此外,估计的掩码$\hat{M}(k,l)$被用作初始估计可靠性的度量。 例如,$\hat{M}(k,l+i)$的值越大,表明第$i$个 TF 单元的本地 SNR 越高。 在这种情况下,相位估计$\bar{\phi^i}(k,l)$更可靠,并且对最终估计$\hat{\phi}(k,l)$的贡献更大。
(3)使用 IFD 进行相位重建:Zheng 和 Zhang (2018) 介绍了使用 IFD 进行相位重建的过程。 首先,估计的$IFD_n$,表示为$\hat{IFD}_n(k,l)$,应该被非规范化并转换为$\hat{IF}(k,l)$。 然后,在频谱掩模$\hat{M}(k,l)$的帮助下,使用噪声相位频谱图和$\hat{IF}(k,l)$重建相位频谱图。 请注意,使用 IFD 进行的相位重建类似于使用 GD 进行的重建。 唯一的区别是前者是沿时间轴重构的,而后者是沿频率轴重构的。
除了仅用GD或仅用IFD对相位进行重构外,我们还提出了以下几种重构组合方案,并在下一节中研究它们的性能。
- 两步重构:在该方案中,我们首先以噪声相位作为初始估计,利用GD/IFD得到初始重构相位。然后将后者作为初始估计,利用IFD/GD得到最终的重构相位。
- 平均重建:在该方案中,我们分别用IFD和GD对初始阶段进行了重建。最后的重构相位是通过对初始相位平均得到的。
结合方案,最后阶段估计$\hat{\phi_S}(k,l)$获得在时间和频率轴。
最后,将重构后的幅度谱和相位谱相结合,得到估计出的纯净语音频谱。
2.4 详细PACDNN架构
我们所提出的PACDNN模型的复合神经网络结构如图6所示。上层由两层LSTM网络组成,每层128个LSTM单元。我们使用Mel-frequency倒谱系数(MFCC)作为LSTM网络的输入,因为就复杂度和性能而言,MFCC是LSTM网络的最佳输入,如Hasannezhad等人(2020b)所示。更具体地说,将MFCC特性与它们的第一和第二差异连接起来,然后归一化为零均值和单位方差。如2.1.1节所述,为了降低LSTM网络复杂度,采用分组策略,将输入层和隐藏层分成K组。实证研究发现,仅对第二层进行K=2的分组,可获得最佳的SE结果。
在图6的底层流中,使用带噪语音STFT幅度作为CNN网络的输入,CNN网络由四个扩张卷积层组成,扩频率分别为1、2、4、8。这些滤波器数分别为16、32、16和8个,具有ReLU激活函数。因为我们想让这个流捕获频谱上下文信息,所以卷积是一维的,核大小随时间为1,随频率维为7。这些层周围的前馈线是残差路径,采用内核大小为 (1, 1) 的卷积层形式,用于改进训练过程。如图所示,将每一层的输出相加(带有跳过连接),得到CNN网络的输出。然后输出到一个注意块,如2.1.2节所述。
然后将LSTM和CNN网络的输出沿通道级联,形成互补特征集。随后,另一个低复杂度的注意力驱动CNN将这个feature set转换成期望的目标。这个CNN由三个卷积层组成,核大小为(1,3),其中通道数为32、16和2。前两层后接ReLU,输出层的激活函数为sigmoid。如前所述,在两个CNN信道中,网络分别估计了频谱掩模和pd。由于这些估计量的结构相似,通过参数共享机制将它们作为同一网络的两个子任务。由于该机制在两个子任务之间引入了正则化效应,因此能够更好地泛化并提高学习效果(Tan和Wang,2019)。在信号重构块中,利用这两个通道的信息重新合成幅值和相位,如第2.3节所述。最后,利用逆短时傅立叶变换和重叠相加运算在时域生成纯净的语音样本。
图6 复合模型架构
3 实验评价
3.1 实验步骤
为了评估提出的PACDNN模型的性能,我们使用了TIMIT数据库(Garofolo et al.,1993)和IEEE语料库(Rothauser,1969)。TIMIT数据集包含630名男性和女性说的6300个话语,代表了美国英语的8个主要方言区,每个都说10个语音丰富的句子。IEEE语料库包含了单个男性说话者的720个话语。对于噪声数据集,我们使用noise-92 (Varga和Steeneken,1993)中的20种噪声(机场、babble、buccaneer1,、汽车、驱逐舰发动机、驱逐舰、演讲、f16、工厂、hfchannel、leopard、m109、机枪、pink、餐馆、街道、地铁、火车、volvo和white)。所有的噪声文件被分成两部分,其中第一部分的随机部分用于训练。在训练阶段,将语音与信噪比分别为-5、0、5和10 dB的噪声加性混合。在测试阶段,从每个数据集中随机选择60个不匹配的语音,并与噪声文件的第二部分的随机部分在不匹配的信噪比级别-6,0,6,12 dB进行混合。此外,从Premium Beat中选取4种不可见的高度非平稳噪声,即咖啡店、繁忙城市街道、汽车内景和街道交通,来评估所提出模型的泛化能力。
采样率设置为 16 kHz,每个混合分为 20 ms 时间帧,帧偏移为 10 ms,即 50% 重叠。 对于每一帧,应用Hanning窗,然后计算 320 点离散傅立叶变换 (DFT); 因此,每帧由 160 个 STFT 系数或频率Bin表示。 STFT 用于提取 26 MFCC,使用合适的梅尔尺度滤波器组。 MFCC 最终与它们的第一次和第二次时间差连接在一起。 因此,用作 LSTM 网络输入的特征向量的总长度为 78(即 26 * 3)。 选择 MSE 作为代价函数,而使用 Adam 优化器(Kingma 和 Ba,2014),以最小化理想(ground truth)与期望掩码和 PD 的估计值之间的误差,如下
$$公式20:MSE=\frac{1}{LK}\sum_l\sum_k[(M(k,l)-\hat{M}(k,l))^2+(PD(k,l)-\hat{PD}(k,l)^2)]$$
其中$L$和$K$分别代表时间帧数和频点数。
语音增强性能根据以下网络客观指标进行评估:PESQ、短时客观可懂度 (STOI) 和分段信噪比 (SSNR) 指标。 PESQ 在质量方面比较增强和干净的语音;它产生 -0.5 到 4.5 之间的分数,其中较高的值对应于更好的质量。 STOI 通过使用清晰语音和增强语音的短时时间包络之间的相关性来衡量语音清晰度;对应的范围在 0 到 1 之间,数值越大对应的清晰度越好。 SSNR 通过计算和平均具有语音活动的片段的加权 SNR 来量化增强语音中的残余噪声量。正如 Hu 和 Loizou (2007) 所述,这三个指标与主观测量高度相关。比较是使用 GeForce RTX 2080 显卡和 2.2 GHz AMD 12 核处理器使用相同的数据集和配置完成的。
3.2 Phase-aware方法评价
提出的DNN旨在同时估计PD和频谱掩模的值。我们将IFD、GD及其组合视为一般PD。此外,我们还研究了四种频谱掩模,即IRM、ORM、PSM和SMM。
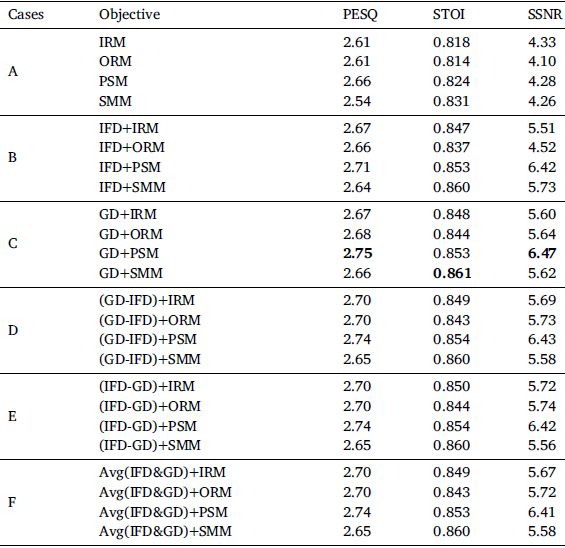
使用不同掩码和pd组合的PACDNN模型的比较性能如表1所示。实验使用TIMIT数据集和餐馆、工厂、街道和嘈杂声作为噪声进行。表中的数字是所有噪音和信噪比水平的平均值。这个表由六个部分组成,如下所述。
A. 这部分展示了在没有PD的情况下,只考虑一个mask作为网络的训练目标时的评价指标分数。可以看出,PSM获得最好的PESQ分数,而SMM和IRM分别导致更好的STOI和SSNR分数。
B. 这部分比较了不同口罩和IFD的使用情况。结果表明,该方法具有相位与幅度同步增强的优点。在这种情况下,IFD+PSM在PESQ和SSNR方面表现较好,而IFD+SMM的STOI得分略好。
C. 这部分比较不同频谱掩模与GD的使用。结果比前面两个场景都好,说明了GD优于IFD。GD+PSM在PESQ和SSNR方面优于其他组合,但STOI不佳。
D. 这一部分研究了两阶段的相位重构,第一阶段使用噪声相位和GD估计对相位进行重构,第二阶段使用重构后的相位和IFD估计得到最终的干净相位估计。
E. 这部分与前一部分相似,但顺序相反,即先利用噪声相位和IFD重构相位,重构后的相位再结合GD估计得到最终的相位估计。
F. 这部分展示了将IFD和GD估计的重构相位的平均值作为清洁相位时的结果。虽然这些组合效果较好,但GD+PSM组合获得了最佳的PESQ和SSNR,GD+SMM组合获得了最佳的STOI。
因此,我们可以得出结论,使用PSM+GD作为训练目标的模型优于其他场景,因此我们在接下来的实验中都采用了它。
表1 不同模型target的比较
3.3 分组LSTM的优点
在 PACDNN 模型中,LSTM 流利用输入语音频谱图的时间上下文信息。 LSTM 是最常见的 RNN 变体,在这项工作中使用它来避免梯度爆炸和消失问题(Chen 和 Wang,2017)。 还考虑了其他 RNN 变体,例如 GRU 和称为 BLSTM 和 BGRU 的双向形式。 此外,我们在 LSTM 流中采用分组策略来降低其复杂性,如第 2.1.1 节所述。 本节使用上述 RNN 变体在有和没有分组策略的情况下评估 PACDNN 模型的性能。
除了第 3.1 节中提到的指标外,我们还比较了这些变化:参数的数量和存储它们所需的内存; 处理一秒钟的输入嘈杂语音的计算时间; 和内存占用,根据所需的浮点运算 (FLOP) 来衡量。 这些额外的测量对于表征 SE 算法的实现复杂性是必不可少的。 这些测量都是在测试阶段进行的,因为经过训练的模型参数将保存在设备硬件中。
图7展示了使用 GRU、LSTM、BGRU、BLSTM 及其分组版本的 PACDNN 模型的性能结果。在该图中,M 和 MB 分别表示百万和兆字节。请注意,数据集与第 3.2 节中的相同,PESQ、STOI 和 SSNR (dB) 的值显示了所有噪声和 SNR 水平的平均改进。如图所示,使用 grouped-LSTM 产生最好的 STOI 和 SSNR 分数,而 LSTM 在 PESQ 分数方面优于其他分数。虽然客观结果没有显示出相当大的差异,但复杂性测量的结果,特别是 FLOP 和参数数量,显示出巨大的变化。就处理时间而言,GRU 显然是最快的,而 BLSTM 是最慢的方法。分组变化导致模型的参数和 FLOP 数量较少,其中,grouped-GRU 需要的参数和 FLOP 数量最少,而 grouped-LSTM 排名第二。考虑到客观语音质量和计算复杂度指标,分组 LSTM 在 PACDNN 模型中的 RNN 变体之间提供了最佳权衡。
图7所示。使用不同RNN变量时PACDNN性能的比较
3.4 以注意力为导向的CNN的好处
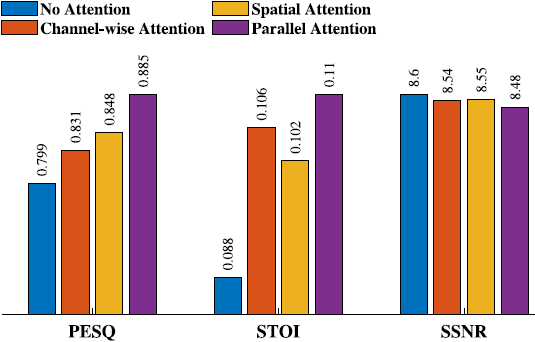
CNN 生成许多特征图,每个特征图都包含一些频谱图特征。这些特征图主要传达噪声或语音信息。在 PACDNN 模型中,注意力技术嵌入在 CNN 中,以重新校准特征图权重并强调承载语音的权重。如第 2.1.2 节所述,我们考虑将三种注意力技术,即通道、空间和并行,嵌入到 PACDNN 模型中,并比较整体模型性能。不同案例的结果,使用与第 3.2 节中相同的数据集,如图8所示,其中的值显示了所有噪声和 SNR 水平的平均改进。考虑到 PESQ 得分,没有注意力的 PACDNN 模型得分最低,而嵌入并行注意力技术的得分最高。关于 STOI,具有并行注意力的模型再次优于其他模型,而没有注意力的模型得分最低。这些结果证明了注意力技术在强调信息特征图方面的有效性。由平均池和最大池组成的并行注意力技术还可以从不同的角度捕捉输入特征图的重要信息,进一步提高其表示能力。关于 SSNR,注意力模型的使用往往会降低可达到的值,尽管会略微降低。
图8 嵌入不同注意方法时PACDNN的性能比较
3.5 回归模型的研究
本节针对 PACDNN 模型的最终回归部分的 MLP 评估第 2.4 节中的 CNN。 MLP 包含三层,每层有 512 个节点,具有 ReLU 激活函数。 还应用了 0.3 的 dropout 以避免过度拟合。 输出层由 322 个节点组成,具有 sigmoid 激活函数来构建所需的掩码和 PD。
两种网络在客观语音质量和计算复杂度指标方面的比较性能如图 9 所示。如图所示,MLP 在客观测量方面产生稍好的结果。 MLP 的这种边际优势源于它的参数数量。在 PACDNN 中使用 MLP 所需的可训练参数大约是使用 CNN 的五倍,这意味着使用 MLP 的模型可以学习训练数据集的更具体模式。值得一提的是,从实现和泛化的角度来看,低复杂度的模型更可取。虽然具有少量参数的模型无法学习训练数据集中有关噪声和语音话语的特定模式或详细信息,但它可以在看不见的声学条件下表现得非常好。除此之外,在模型中使用 CNN 和 MLP 分别需要 0.74 MB 和 3.82 MB 的内存来存储固定的模型参数,这与参数的数量成正比。虽然 MLP 中的基本计算在概念上比 CNN 更简单,但前者仍然需要比前者多 1.46 倍的 FLOP,这是由于模型参数数量较多。最后,执行大量矩阵乘法的 CNN 的计算时间略高于 MLP。
图9所示。比较使用CNN或MPL进行最终回归时的PACDNN模型性能
3.6 与其他基于DNN的方法的比较
本节将提出的 PACDNN 模型与 SE 任务中一些著名的 DNN 模型进行比较。 所选模型具有中等复杂性。 所有选定的方法都考虑了 SE 的相位信息以及幅度增强。 所有模型,包括 PACDNN,都在相同条件下使用相同的数据集进行训练和测试,以确保公平比较。 选择的方法总结如下
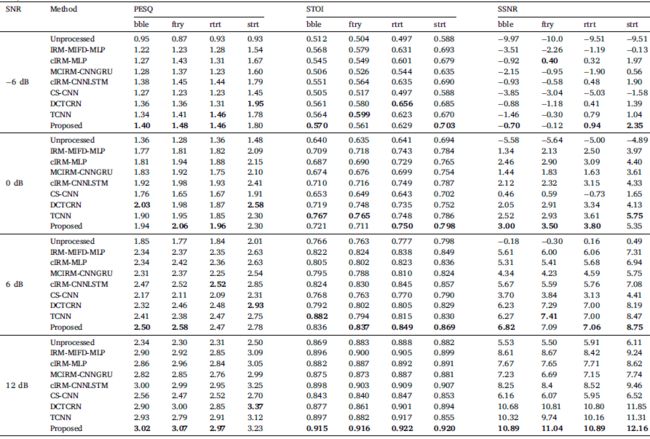
表2 不同方法与 TIMIT 数据集中未见男性话语的比较
1. IRM-MIFD-MLP(Zheng 和 Zhang,2018 年):在这种多目标 DNN 方法中采用了具有三层的 MLP。每个隐藏层包含 1024 个具有 ReLU 激活函数的节点,而输出层包含 512 个具有 sigmoid 激活函数的节点。 IRM 和 IFD 被用作训练目标。
2. cIRM-MLP (Williamson et al.,2015):在这种方法中,使用三层 MLP 来近似 cIRM。每层有 1024 个具有 ReLU 激活功能的节点。具有线性激活函数的输出层估计 cIRM 的实部和虚部。网络的输入是一组互补的声学特征。为了合并时间信息,来自 5 帧的特征被连接起来并立即馈送到网络。
3. MCIRM-CNNGRU (Hasannezhad et al.,2020a):在这种方法中,混合模型用于估计修改后的 cIRM 的实部和虚部。该网络由用于特征提取的 CNN 和用于回归的 GRU 网络组成。复杂的频谱图用作输入,具有线性激活函数的 322 节点输出层生成所需的掩码值。
4. cIRM-CNNLSTM (Hasannezhad et al.,2020b):在这里,一个 CNN、LSTM 和 MLP 被集成来估计 cIRM。特征提取由 CNN 和 LSTM 网络执行,而回归由 MLP 完成,MLP 将特征映射到 cIRM 的实部和虚部。
5. CS-CNN (Ouyang et al.,2019):利用全卷积 CNN 来估计干净语音复谱图的实部和虚部。输入由呈现给网络的 13 帧噪声语音复合频谱图组成。输出的中间帧(第 7 帧)被认为是增强的输出帧。
6. DCTCRN (Li et al.,2021):与之前的方法都在频域执行不同,该方法在离散余弦变换(DCT)域完成语音增强,从而同时增强幅度和相位。输入是短时 DCT (STDCT),训练目标是包含隐式相位信息的比率掩码。 CRN 用作学习机来执行输入 STDCT 和比率掩码之间的映射。
7. TCNN(Pandey 和 Wang,2019 年):该方法旨在在时域中执行,其中时间卷积神经网络 (TCNN) 以及具有时间卷积网络的嵌入式编码器解码器架构用于直接映射嘈杂的讲话干净的。
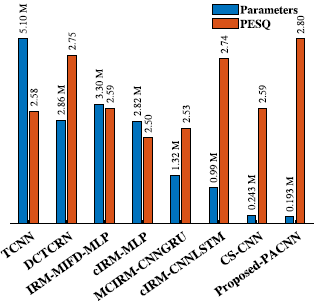
图 10 说明了每种方法的可训练参数的数量以及使用 TIMIT 数据集评估的不同噪声和 SNR 水平上处理语音的平均 PESQ 分数。如图所示,TCNN 和 DCTCRN 具有大量的模型参数;因此,它们具有很高的计算复杂度。正如预期的那样,基于 MLP 的模型,即 IRM-MIFD-MLP 和 cIRM-MLP,也包含大量模型参数,因此需要大内存来存储它们。值得一提的是,TCNN 和 DCTCRN 的计算量远高于基于 MLP 的模型,因为前者包含许多卷积操作。另外两个混合模型,即 MCIRM-CNNGRU 和 cIRM-CNNLSTM,具有相当数量的参数,每个都在 100 万左右。参数数量最少的是 CS-CNN 和所提出的模型,后者需要的参数略少。尽管 PACDNN 的模型参数数量仅为 TCNN 的 3% 和 DCTCRN 的 6%,但它在 SE 任务中的表现优于所有上述模型,如图所示,下面将进一步讨论。
图10所示。比较不同方法的可训练参数个数和平均PESQ得分
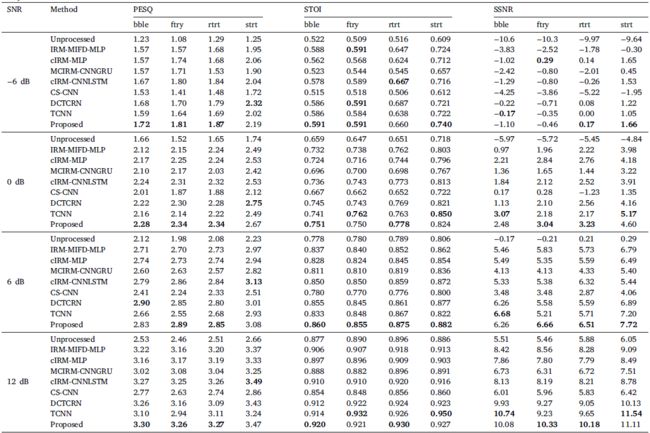
由于男性和女性之间的语音特征不同,我们分别评估不同的模型以显示所需模型对不同性别的泛化能力。来自 TIMIT 数据集的男性测试话语的比较结果如表 2 所示,其中 bble、ftry、rtrt 和 strt 分别表示 babble、工厂、餐厅和街道噪音。如图所示,所提出的模型在各种客观质量指标方面优于所有其他模型,除了少数情况,包括 SNR 水平为 -6 和 0 dB 的街道噪声的 PESQ,其中 DCTCRN 给出略高的分数和 SNR 水平6 和 12 dB,其中 cIRM-CNNLSTM 的得分略高。此外,在 0 和 12 dB 的 SNR 水平下,TCNN 对街道和工厂噪声产生的 STOI 略好一些。此外,TCNN 在 SNR 级别为 0 和 12 dB 时为 babble 和街道噪声提供了更好的 SSNR 分数。表 3 说明了来自 TIMIT 数据集的女性话语的结果。同样,我们可以看到,所提出的模型在几乎所有情况下都优于其他模型,除了少数 SNR 级别为 -6 和 0 的 STOI 情况,其中 DCTCRN 和 TCNN 给出了更好的结果。
表3 不同方法对来自TIMIT数据集的女性话语的比较
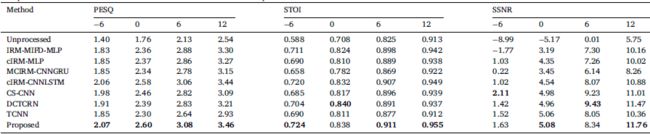
在另一个实验中,我们比较了 IEEE 语料库上的不同方法,其中 20 种噪声与选定的话语混合,在训练和测试阶段之间具有不匹配的 SNR 水平。 从表 4 中可以看出,表 4 显示了 PESQ、STOI 和 SSNR 指标的平均分数,除了 SNR 水平为 -6 和 6 dB 的 SSNR 分数外,所提出的模型在所有情况下都明显优于所有其他方法,其中 CS-CNN 和 DCTCRN 给出了稍微好一点的结果。 该实验表明,尽管所提出的模型具有非常少的参数,但它在不同的噪声条件下都能表现良好。
表4 不同方法对来自IEEE语料库和20种不同噪声的未见话语的比较
在与表 4 相同的训练条件下,我们测试了不同的方法,将看不见的高度非平稳噪声与来自 IEEE 语料库的看不见的话语以无与伦比的 SNR 水平混合在一起,以评估它们在看不见的条件下的泛化能力。 比较结果如表 5 所示,其中 bscs、cair、cfsp 和 sttc 表示咖啡店、繁忙的城市街道、汽车内饰和街道交通。 可以看出,除了少数情况外,所提出的模型总体上优于所有其他方法。 该实验表明,所提出的模型具有很好的泛化能力,这得益于其精心设计和少量参数,使其不学习训练数据集的特定模式,而是依赖于语音和噪声的一般信息。
表5 不同方法对混合了不可见噪声的IEEE语料库中不可见话语在不匹配信噪比水平下的比较
如 Pandey 和 Wang (2020) 所示,当训练和测试数据集不同时,DNN 方法的性能可能会显着下降,尤其是在低 SNR 水平下。 这项研究表明,一些众所周知但高度复杂的 SE 方法在未经训练的语料库上表现不佳。 在最后一个实验中,我们比较了不同方法的跨语料库泛化能力。 为此,我们使用 TIMIT 数据集训练了不同的模型,并使用 IEEE 语料库对其进行了测试。 表 6 显示了不同 SNR 水平的结果,表明当训练和测试数据集不同时,所提出的模型优于其他模型,除了 SNR 6 dB 时,其他方法会产生更好的结果。 此外,图 11 显示了一个样本频谱图,显示了不同方法的差异。 因此,我们可以得出结论,所提出的 PACDNN 模型为看不见的数据集提供了非常好的泛化能力。
表6 跨语料库评估,其中分别使用TIMIT数据集和IEEE语料库完成训练和测试
图11所示。使用不同模型说明增强语音的短时傅立叶变换幅度(对数尺度)。用TIMIT数据集对模型进行训练,用IEEE语料库中的话语对模型进行测试。在0分贝的信噪比水平下,声音与街道噪音混合。
4 结论
本文提出了一种称为 PACDNN 的相位感知复合深度神经网络,用于语音增强,其中语音幅度和相位都得到了增强。具体来说,我们设计了一种基于掩蔽的方法来增强幅度并使用相位导数来重建干净的语音相位。由于频谱掩模和相位导数的结构相似性,使用单个神经网络通过同时参数共享来估计两种信息类型。所提出的网络集成了改进的 LSTM 和 CNN,它们并行执行以利用一组互补的特征。在客观语音质量和计算复杂性测量方面研究和比较了不同的潜在 DNN 解决方案,以优化特征和所需目标之间的最终回归。通过一系列广泛的实验,对得到的 PACDNN 模型进行了评估,并与使用不同数据集和客观测量的几种已知的基于 DNN 的 SE 方法进行了比较。特别是,研究了所提出的模型在处理看不见的噪声条件、跨语料库泛化和测试和训练中不匹配的 SNR 水平方面的能力,证明了 PACDNN 在 SE 应用中优于其他方法的优势,尽管其复杂性较低.
参考文献
Abbaszadeh,P.,2016. Improving hydrological process modeling using optimized threshold-based wavelet de-noising technique. Water Resour. Manag. 30 (5),1701 1721.
Abd El-Fattah,M.,Dessouky,M.I.,Diab,S.M.,Abd El-Samie,F.E.-S.,2008. Speech enhancement using an adaptive wiener filtering approach. Prog. Electromagn. Res. 4,167 184.
Agnew,J.,Thornton,J.M.,2000. Just noticeable and objectionable group delays in digital hearing aids. J. Am. Acad. Audiol. 11 (6),330 336.
Chen,J.,Wang,D.,2017. Long short-term memory for speaker generalization in supervised speech separation. J. Acoust. Soc. Am. 141 (6),4705 4714.
Cui,X.,Chen,Z.,Yin,F.,2020. Speech enhancement based on simple recurrent unit network. Appl. Acoust. 157,107019.
Dey,R.,Salemt,F.M.,2017. Gate-variants of gated recurrent unit (GRU) neural networks. In: Int. Midwest Symposium on Circuits and Systems. MWSCAS,IEEE,pp. 1597 1600.
Erdogan,H.,Hershey,J.R.,Watanabe,S.,Le Roux,J.,2015. Phase-sensitive and recognition-boosted speech separation using deep recurrent neural networks. In: IEEE Int. Conf. on Acoustics,Speech and Signal Processing. ICASSP,pp. 708 712.
Fu,S.-W.,Hu,T.-y.,Tsao,Y.,Lu,X.,2017a. Complex spectrogram enhancement by convolutional neural network with multi-metrics learning. In: Int. Workshop on Machine Learning for Signal Processing. MLSP,IEEE,pp. 1 6.
Fu,S.-W.,Tsao,Y.,Lu,X.,Kawai,H.,2017. Raw waveform-based speech enhancement by fully convolutional networks. In: IEEE Asia-Pacific Signal and Information Processing Association Annual Summit and Conf. APSIPA ASC,pp. 006–012.
Gao,F.,Wu,L.,Zhao,L.,Qin,T.,Cheng,X.,Liu,T.-Y.,2018. Efficient sequence learning with group recurrent networks. In: Proc. of Conf. of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies,Vol. 1. pp. 799–808,Long Papers.
Garofolo,J.S.,Lamel,L.F.,Fisher,W.M.,Fiscus,J.G.,Pallett,D.S.,1993. DARPA TIMIT Acoustic-Phonetic Continuous Speech Corpus CD-ROM. NIST speech disc 1-1.1. NASA STI/Recon Technical Report,vol. 93.
Hasannezhad,M.,Ouyang,Z.,Zhu,W.-P.,Champagne,B.,2020a. An integrated CNNgru framework for complex ratio mask estimation in speech enhancement. In: IEEE Asia-Pacific Signal and Information Processing Association Annual Summit and Conf. APSIPA ASC,pp. 764–768.
Hasannezhad,M.,Ouyang,Z.,Zhu,W.-P.,Champagne,B.,2020b. Speech separation using a composite model for complex mask estimation. In: Int. Midwest Symposium on Circuits and Systems. MWSCAS,IEEE,pp. 578–581.
Hasannezhad,M.,Zhu,W.-P.,Champagne,B.,2021. A novel low-complexity attentiondriven composite model for speech enhancement. In: International Symposium on Circuits and Systems. ISCAS,IEEE,pp. 1–5.
Hegde,R.M.,Murthy,H.A.,Gadde,V.R.R.,2007. Significance of the modified group delay feature in speech recognition. IEEE Trans. Audio,Speech,Lang. Process. 15(1),190–202.
Hsieh,T.-A.,Wang,H.-M.,Lu,X.,Tsao,Y.,2020. WaveCRN: An efficient convolutional recurrent neural network for end-to-end speech enhancement. arXiv preprint arXiv: 2004.04098.
Hu,Y.,Liu,Y.,Lv,S.,Xing,M.,Zhang,S.,Fu,Y.,Wu,J.,Zhang,B.,Xie,L.,2020. DCCRN: deep complex convolution recurrent network for phase-aware speech enhancement. arXiv preprint arXiv:2008.00264.
Hu,Y.,Loizou,P.C.,2007. Evaluation of objective quality measures for speech enhancement. IEEE/ACM Trans. Audio,Speech,Lang. Process. 16 (1),229–238.
Hu,J.,Shen,L.,Sun,G.,2018. Squeeze-and-excitation networks. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. pp. 7132–7141.
Kingma,D.P.,Ba,J.,2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
Krawczyk,M.,Gerkmann,T.,2014. STFT phase reconstruction in voiced speech for an improved single-channel speech enhancement. IEEE/ACM Trans. Audio,Speech,Lang. Process. 22 (12),1931–1940.
Li,Q.,Gao,F.,Guan,H.,Ma,K.,2021. Real-time monaural speech enhancement with short-time discrete cosine transform. arXiv preprint arXiv:2102.04629.
Liang,S.,Liu,W.,Jiang,W.,Xue,W.,2013. The optimal ratio time-frequency mask for speech separation in terms of the signal-to-noise ratio. J. Acoust. Soc. Am. 134 (5),EL452–EL458.
Martin,R.,May 2002. Speech enhancement using MMSE short time spectral estimation with gamma distributed speech priors. In: IEEE Int. Conf. on Acoustics,Speech,and Signal Processing,Vol. 1. pp. I–253.
Mowlaee,P.,Saeidi,R.,2014. Time-frequency constraints for phase estimation in singlechannel speech enhancement. In: Int. Workshop on Acoustic Signal Enhancement. IWAENC,IEEE,pp. 337–341.
Oord,A.v.d.,Dieleman,S.,Zen,H.,Simonyan,K.,Vinyals,O.,Graves,A.,Kalchbrenner,N.,Senior,A.,Kavukcuoglu,K.,2016. Wavenet: a generative model for raw audio. arXiv preprint arXiv:1609.03499.
Ouyang,Z.,Yu,H.,Zhu,W.-P.,Champagne,B.,2019. A fully convolutional neural network for complex spectrogram processing in speech enhancement. In: IEEE Int. Conf. on Acoustics,Speech and Signal Processing. ICASSP,pp. 5756–5760.
Pandey,A.,Wang,D.,2019. TCNN: Temporal convolutional neural network for real-time speech enhancement in the time domain. In: ICASSP 2019-2019 IEEE International Conference on Acoustics,Speech and Signal Processing. ICASSP,IEEE,pp. 6875–6879.
Pandey,A.,Wang,D.,2020. Learning complex spectral mapping for speech enhancement with improved cross-corpus generalization. Proc. Interspeech 2020 4511–4515.
Parchami,M.,Zhu,W.-P.,Champagne,B.,Plourde,E.,2016. Recent developments in speech enhancement in the short-time Fourier transform domain. IEEE Circuits Syst. Mag. 16 (3),45–77.
Park,S.R.,Lee,J.,2016. A fully convolutional neural network for speech enhancement. arXiv preprint arXiv:1609.07132.
Prasad,V.K.,Nagarajan,T.,Murthy,H.A.,2004. Automatic segmentation of continuous speech using minimum phase group delay functions. Speech Commun. 42 (3–4),429–446.
Premium Beat,www.premiumbeat.com.
Rothauser,E.,1969. IEEE Recommended practice for speech quality measurements. IEEE Trans. Audio Electroacoust. 17,225–246.
Roy,A.G.,Navab,N.,Wachinger,C.,2018. Concurrent Spatial and Channel ‘Squeeze & Excitation’ in Fully Convolutional Networks. In: Int. Conf. on Medical Image Computing and Computer-Assisted Intervention,pp. 421–429.
Shifas,M.P.,Claudio,S.,Stylianou,Y.,et al.,2020. A fully recurrent feature extraction for single channel speech enhancement. arXiv preprint arXiv:2006.05233.
Srinivasan,S.,Roman,N.,Wang,D.,2006. Binary and ratio time-frequency masks for robust speech recognition. Speech Commun. 48 (11),1486–1501.
Stark,A.P.,Paliwal,K.K.,2008. Speech analysis using instantaneous frequency deviation. In: INTERSPEECH.
Strake,M.,Defraene,B.,Fluyt,K.,Tirry,W.,Fingscheidt,T.,2020. Fully convolutional recurrent networks for speech enhancement. In: IEEE Int. Conf. on Acoustics,Speech and Signal Processing. ICASSP,pp. 6674–6678.
Takamichi,S.,Saito,Y.,Takamune,N.,Kitamura,D.,Saruwatari,H.,2018. Phase reconstruction from amplitude spectrograms based on von-Mises-distribution deep neural network. In: 2018 16th International Workshop on Acoustic Signal Enhancement. IWAENC,IEEE,pp. 286–290.
Takamichi,S.,Saito,Y.,Takamune,N.,Kitamura,D.,Saruwatari,H.,2020. Phase reconstruction from amplitude spectrograms based on directional-statistics deep neural networks. Signal Process. 169,107368.
Tan,K.,Wang,D.,2018. A convolutional recurrent neural network for real-time speech enhancement.. In: INTERSPEECH. pp. 3229–3233.
Tan,K.,Wang,D.,2019. Learning complex spectral mapping with gated convolutional recurrent networks for monaural speech enhancement. IEEE/ACM Trans. Audio,Speech,Lang. Process. 28,380–390.
Varga,A.,Steeneken,H.J.,1993. Assessment for automatic speech recognition: Ii. NOISEX-92: A database and an experiment to study the effect of additive noise on speech recognition systems. Speech Commun. 12 (3),247–251.
Wang,D.,Chen,J.,2018. Supervised speech separation based on deep learning: An overview. IEEE/ACM Trans. Audio,Speech,Lang. Process. 26 (10),1702–1726.
Wang,Y.,Narayanan,A.,Wang,D.,2014. On training targets for supervised speech separation. IEEE/ACM Trans. Audio,Speech,Lang. Process. 22 (12),1849–1858.
Williamson,D.S.,Wang,Y.,Wang,D.,2015. Complex ratio masking for monaural speech separation. IEEE/ACM Trans. Audio,Speech,Lang. Process. 24 (3),483–492.
Woo,S.,Park,J.,Lee,J.-Y.,So Kweon,I.,2018. CBAM: Convolutional block attention module. In: Proc. of the European Conf. on Computer Vision. ECCV,pp. 3–19.
Xu,Y.,Du,J.,Dai,L.-R.,Lee,C.-H.,2014. A regression approach to speech enhancement based on deep neural networks. IEEE/ACM Trans. Audio,Speech,Lang. Process. 23 (1),7–19.
Yin,D.,Luo,C.,Xiong,Z.,Zeng,W.,2020. PHASEN: A phase-and-harmonics-aware speech enhancement network.. In: Association for the Advancement of Artificial Intelligence. AAAI,pp. 9458–9465.
Yu,F.,Koltun,V.,2015. Multi-scale context aggregation by dilated convolutions. arXiv preprint arXiv:1511.07122.
Zhao,H.,Zarar,S.,Tashev,I.,Lee,C.-H.,2018. Convolutional-recurrent neural networks for speech enhancement. In: IEEE Int. Conf. on Acoustics,Speech and Signal Processing. ICASSP,pp. 2401–2405.
Zheng,N.,Zhang,X.-L.,2018. Phase-aware speech enhancement based on deep neural networks. IEEE/ACM Trans. Audio,Speech,Lang. Process. 27 (1),63–76.