【阅读笔记】Towards Efficient and Privacy-preserving Federated Deep Learning
Towards Efficient and Privacy-preserving Federated Deep Learning
- 前言
- 一、论文解析
-
- Abstract
- 1. INTRODUCTION
- 2. SYSTEM MODEL AND THREAT MODEL
-
- 2.1 System Model
- 2.2 Threat Model
- 3. PRELIMINARIES
-
- 3.1 Neural Network and Federated Deep Learning
- 3.2 Additively Homomorphic Encryption
- 3.3 ϵ- Differential Privacy and Laplace Mechanism
- 4. PROPOSED SCHEME
-
- 4.1 Overview of Gradients Aggregation Scheme
- 4.2 Efficient and Privacy-preserving Federated Deep Learning
- 5. SECURITY ANALYSIS
-
- 5.1 Security against the cloud server
- 5.2 Security against the cloud server and compromised users
- 6. PERFORMANCE EVALUATION
-
- 6.1 Communication overhead
- 6.2 Computational cost
- 6.3 Accuracy
- 7. CONCLUSION
- 二、论文总结
- 三、个人感悟
前言
一篇来自通信领域顶级会议ICC的文章,阅读这篇文章的目的是因为这篇文章创新性使用了混合隐私保护技术,通过结合同态加密和差分隐私,保证了数据效用的同时,又降低了通信成本,虽然是2019年的文章,但是其中的思想还是对我未来的研究有很大的帮助,希望能通过这篇文章的学习了解更多混合加密技术核心问题。
一、论文解析
Abstract
摘要部分首先提及传统的深度学习通过中心化收集数据,在各大领域进行应用,分布式深度学习可以通过数据本地训练,传递中间参数来达到提高效率和安全性的作用,但是这仍会受到敌手的推理攻击,于是本文结合加法同态加密和差分隐私,提出了一种基于随机梯度下降法的高效、私有化的联邦深度学习协议。最后通过实验表明,该方案有较高的效率和准确性。
1. INTRODUCTION
深度学习广泛应用,但是存在隐私泄露风险,因此联邦学习孕育而生,通过分布式训练,获取中间值的方式保证用户隐私。即便如此,敌手仍能通过梯度揭示个人信息。现有的解决方案包括基于选择性随机梯度下降的协作式深度学习模型,附加同态加密的深度学习系统,但是前者容易受到好奇的服务器影响,后者通信计算开销大。于是就有了本文作者的将加法同态加密与差分隐私相结合,一种基于随机梯度下降方法的高效且隐私保护的联邦深度学习方案。它的优势如下:
- 轻量级,高效安全,支持大规模应用的联邦学习。
- 使用基于拉普拉斯机制的差分隐私。
- 隐私损失可以忽略不计,较高效率和准确性。
2. SYSTEM MODEL AND THREAT MODEL
2.1 System Model
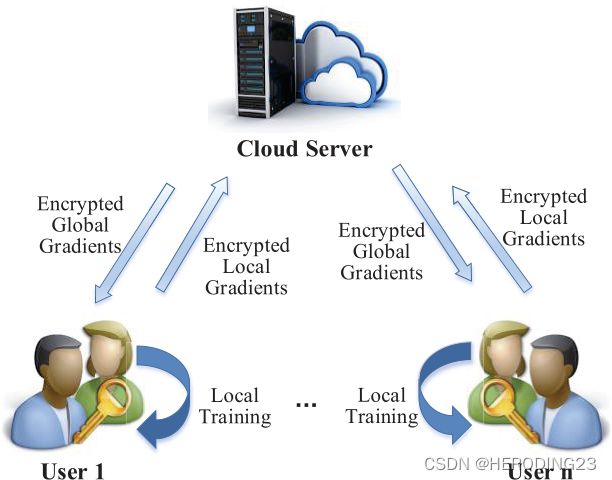
如图1,系统由多个参与方和一个云服务器组成,假设所有参与方共同训练一个神经网络模型。
- 参与方将本地训练得到的梯度上传到云服务器,提交之前为了安全,对数据进行干扰和加密。
- 云服务器在加密的梯度上计算全局梯度,然后广播给参与方,最后通过迭代合作,建立神经网络模型。
2.2 Threat Model
云服务器被认为是诚实但好奇的,会从参与方的输入中提取信息,另一个方面,该协议要能容忍服务器和多个参与方之间的共谋,所以要求服务器不能从本地梯度中获取任何有用信息,除非加密的聚合结果。
3. PRELIMINARIES
这一节简单介绍神经网络并讨论在本文重要作用的密码原语。
3.1 Neural Network and Federated Deep Learning
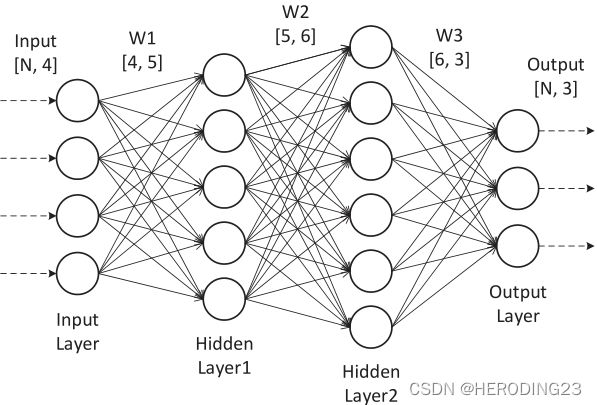
图2展示了一个神经网络的构成,包括输入层,多个隐藏层和一个输出层,每个层都由多个神经元组成,输入的数据通过仿射变换和非线性激活函数的处理在每一层中进行传播,对于每次的输出结果通过随机梯度下降方法进行更新,损失函数用作预测结果和实际的差距。
联邦学习的过程在上文有所提及,这里就不再赘述。
3.2 Additively Homomorphic Encryption
加性同态加密保证多个密文运算后结果可以成功解密。这样参与方将加密数据外包给云服务器处理也不用担心隐私泄露。比如给定明文 m 1 m_{1} m1、 m 2 m_{2} m2,有
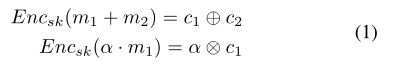 c 1 c_{1} c1和 c 2 c_{2} c2都是密文。
c 1 c_{1} c1和 c 2 c_{2} c2都是密文。
3.3 ϵ- Differential Privacy and Laplace Mechanism
首先是差分隐私的概念,其实就是两个相邻的数据集(只要改变任何一个的数据就可以变为另一个)如果满足
![]() 就说明其是满足ϵ-DP的,一般来说,ϵ越小,提供的隐私保护级别就会越高,但是相应的准确率会降低。
就说明其是满足ϵ-DP的,一般来说,ϵ越小,提供的隐私保护级别就会越高,但是相应的准确率会降低。
拉普拉斯机制。对于查询函数f,如果下列公式成立,则机制f′满足ϵ-DP
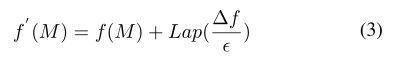 拉普拉斯机制基于 L 1 L_{1} L1敏感度的,可以理解为数据向量之间的距离,这也是公式中的 △ f \bigtriangleup f △f,(3)式中的Lap表示的就是满足拉普拉斯分布获得的值。
拉普拉斯机制基于 L 1 L_{1} L1敏感度的,可以理解为数据向量之间的距离,这也是公式中的 △ f \bigtriangleup f △f,(3)式中的Lap表示的就是满足拉普拉斯分布获得的值。
4. PROPOSED SCHEME
这一部分就是介绍基于混合机制和随机梯度下降法的联邦学习方案。
4.1 Overview of Gradients Aggregation Scheme
同态加密被广泛运用实现密文的加密聚合,但是它会显著增加计算和通信开销。但是PPDM(对称加法同态加密)相比具有更高的效率,此外,为了进一步提高安全性和容忍参与方退出,采用了差分隐私。
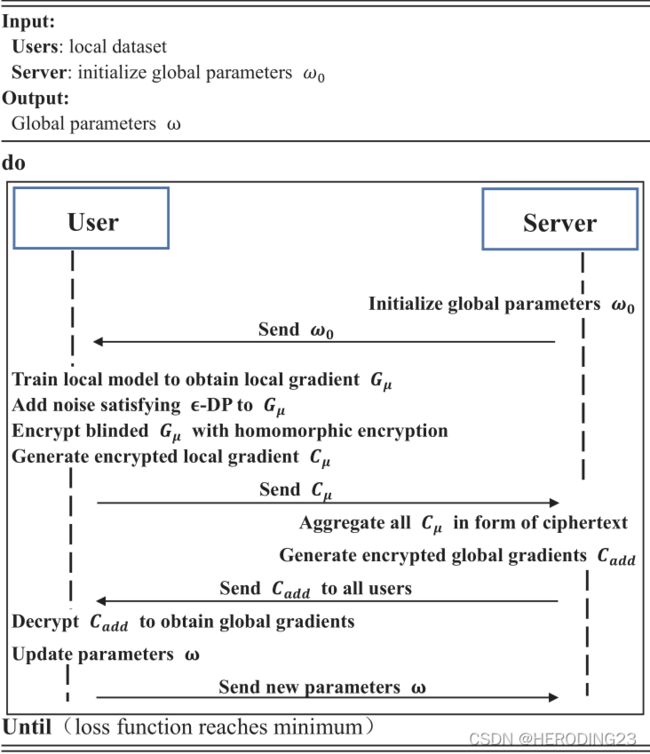 如图三,对于每一个epoch,每个参与方µ使用一小批局部数据集学习模型,并计算局部梯度Gµ。为了保护隐私,在数据中加入拉普拉斯噪声,并用同态加密处理,在接收到所哟偶加密梯度后,云服务器聚合:
如图三,对于每一个epoch,每个参与方µ使用一小批局部数据集学习模型,并计算局部梯度Gµ。为了保护隐私,在数据中加入拉普拉斯噪声,并用同态加密处理,在接收到所哟偶加密梯度后,云服务器聚合:
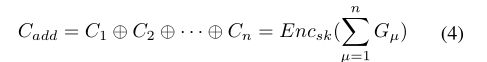
由于拉普拉斯分布的对称性,噪声几乎被消除。最终,参与方解密从服务器返回的加密全局梯度,然后更新参数ω。通过这种方式,整个神经网络将在云服务器和多个用户之间不断迭代建立。
4.2 Efficient and Privacy-preserving Federated Deep Learning
初始化: 原始的全局参数ω0和学习率η由云服务器初始化。此外,给定安全参数λ,生成密钥sk并将其分配给所有参与方,其中sk由两个大素数p,q(|p |=|q |=λ)组成。公共参数为N=pq。
加密: 为保护参与方信息隐私,所有参与方选中相同的隐私预算ϵ。
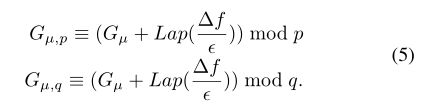
其中Gµ是本地梯度。 我们假设每个梯度为0≤ G≤ 1.利用最小-最大归一化,以及∆f可以设置为1。
然后,使用秘钥p,q对局部梯度进行加密,如下所示:
![]()
其中 p − 1 p^{-1} p−1、 q − 1 q^{-1} q−1表示p和q在 Z ∗ q \mathbb{Z}_{*}^{q} Z∗q中的倒数, Z ∗ q \mathbb{Z}_{*}^{q} Z∗q和加密的本地梯度Cµ将被发送到云服务器。
安全聚合:
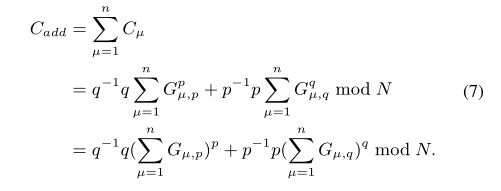
上式等式成立因为:

其中f(G)表示:
![]()
最后服务器广播全局梯度 C a d d C_{add} Cadd。
解密: 参与方收到全局参数后解密,
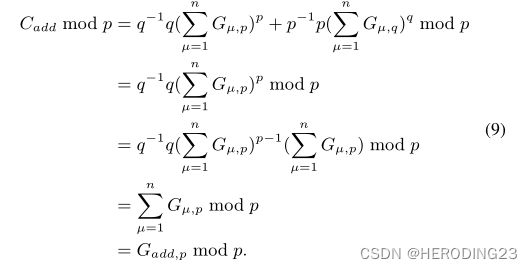
类似的,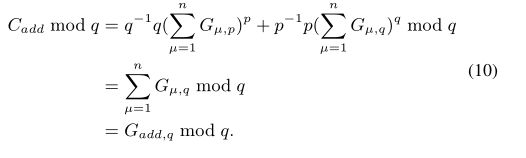 根据欧拉定理和辗转相除法,上述公式成立。然后,参与方可以用中国剩余定理恢复全局梯度 G a d d G_{add} Gadd,计算此同余表达式:
根据欧拉定理和辗转相除法,上述公式成立。然后,参与方可以用中国剩余定理恢复全局梯度 G a d d G_{add} Gadd,计算此同余表达式:
![]()
其中![]() 由于参与方数量庞大,所以可以忍受参与方退出。所以对消除扰动过程的噪声几乎没有影响,即 G a d d G_{add} Gadd近似等于 ∑ μ = 1 n G μ \sum _{\mu=1}^{n}G_{\mu} ∑μ=1nGμ。最终,参与方根据ω更新参数ω←ω− η N \frac{η}{N} Nη Gadd,其中N来自云服务器。然后重复执行,直到达到终止条件,即之前定义的损失函数的最小值。
由于参与方数量庞大,所以可以忍受参与方退出。所以对消除扰动过程的噪声几乎没有影响,即 G a d d G_{add} Gadd近似等于 ∑ μ = 1 n G μ \sum _{\mu=1}^{n}G_{\mu} ∑μ=1nGμ。最终,参与方根据ω更新参数ω←ω− η N \frac{η}{N} Nη Gadd,其中N来自云服务器。然后重复执行,直到达到终止条件,即之前定义的损失函数的最小值。
5. SECURITY ANALYSIS
本文主要关注于参与方本地梯度的隐私泄露问题。
5.1 Security against the cloud server
定理: 只要上述附加同态加密方案是CPA安全的,方案就不会显示关于单个局部梯度的比特信息。
证明: 本文的加密方案是基于大整数分解问题,
并且已经被证明是安全的。因此,模型很好地保护了参与方个体本地梯度的机密性。
5.2 Security against the cloud server and compromised users
考虑到现实问题, 对手可能会危及某些参与方,从而窃取系统的私钥和诚实参与方的隐私。而差分隐私可以提供严格的隐私保障。
定理: 拉普拉斯机制G′µ=Gµ+Lap( △ G ϵ \frac{\bigtriangleup G}{\epsilon } ϵ△G)在梯度扰动中保持Gµ的ϵ-微分隐私。
证明: 设 χ \chi χ为注入Gµ的噪声, χ \chi χ~Lap( △ G ϵ \frac{\bigtriangleup G}{\epsilon } ϵ△G),设 M M M和 M ‾ \overline{M} M是相邻的数据集,有:
 类似的,
类似的,
![]() 因此,
因此,
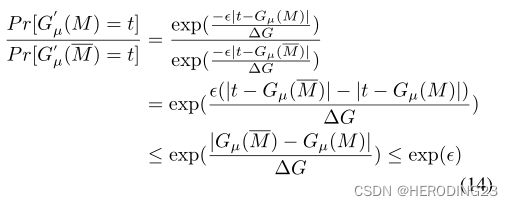
因此,梯度扰动保留了ϵ-DP,该方案可以容忍服务器与任何参与方合谋,但不能推断任何有用的信息。
6. PERFORMANCE EVALUATION
实验部分是与最新的PPDL进行比较,评估方案的准确性和通信计算开销,其中采用了配对加密作为底层结构。
6.1 Communication overhead
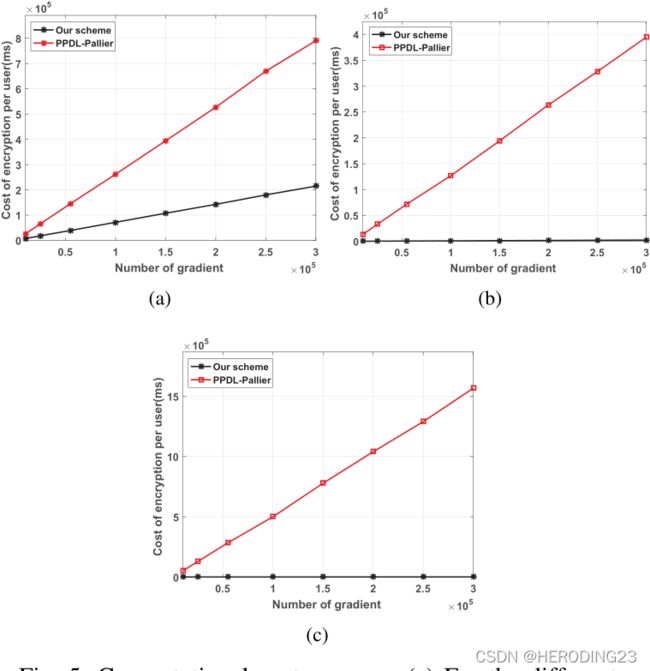
通信开销部分,首先实验在MNIST数据集上使用TensorFlow运行卷积网络,梯度来自6万个28×28的图像。图4显示了一次迭代下云服务器的通信开销。显然,随着梯度的数量递增,方案开销是PPDL的50倍小。其中一个主要原因是使用Paillier同态加密后密文数量快速增长。同样,随着用户数量增加,通信开销就大大低于PPDL。
6.2 Computational cost
接着,本文分别讨论了方案在加密、聚合、解密阶段的计算开销。如上图所示,随着梯度数量的增加,加密的成本显著低于PPDL。此外,我们的聚合和解密成本似乎几乎为零,因为它们只包含很少的乘法和加法运算。所以,本文提出的方案支持大规模参与方的场景。
6.3 Accuracy
在评估中,研究了用户数量和隐私预算对训练模型分类准确性的影响。在非私有卷积模型的分类下,准确率为98.5%,在私有卷积模型下,当用户数量和隐私预算分别为300和1时,本文的解决方案将实现98.1%的准确率。理论上,由于拉普拉斯噪声的对称性,大部分参与方的噪声会消除。因此,本文提出的方案能够保持较高的准确性。
7. CONCLUSION
在本文中,作者将加法同态加密与差分隐私相结合,提出了一种高效且保护隐私的联邦深度学习方案。作者采用轻量级加法同态加密来提高效率。然后,为了防止云服务器和多个用户之间的共谋威胁,进一步使用基于对称拉普拉斯机制的差分隐私技术来扰动用户的原始局部梯度。最后,大量实验表明,该方案在非私有训练模型下具有较高的效率和准确性。在未来的工作中,作者将采用多密钥加密方案,以减少计算开销。
二、论文总结
本文创新性采用了轻量级的加法同态加密技术和基于拉普拉斯机制的差分隐私技术,实现了一种基于随机梯度下降方法的高效且隐私保护的联邦深度学习方案。本文从联邦学习的痛点出发(即梯度信息仍容易受到敌手的推理攻击),考虑到通信和计算开销,采用了混合机制的隐私保护方法,并证明了混合机制的安全性和隐私性。在实验部分,通过与PPDL模型的对比,证明了加法同态加密的通信开销远远低于PPDL(50倍smaller),计算开销也远小于PPDL,在准确度方面,即使加入了拉普拉斯噪声, 与非隐私的准确度相比几乎无异(相差0.4%),这利用了拉普拉斯机制的对称性,大部分参与方的噪声会消除。总而言之,本文提出的方案支持大规模参与方的场景,轻量级且高效。
三、个人感悟
这是一篇对我毕业设计工作启发极大的论文,包括拉普拉斯机制的对称性可以在最终的聚合时消除噪声的操作,加法同态加密的轻量性,以及实验的准确性。下一步我的工作就是复现该论文,以期达到类似的效果。